ESEMPI DI FUNZIONI

matematica

ESEMPI DI FUNZIONI

y=xe^x

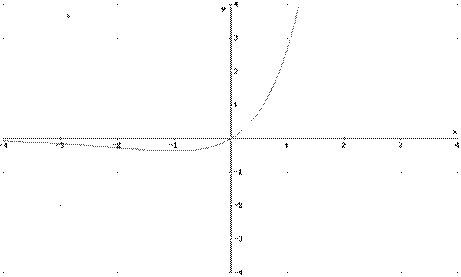
Il campo di esitenza della funzione è tutto l'insieme dei numeri reali; la funzione è pos 939j91j itiva per x>0 e negativa quando x<0; per x->+inf  la funzione tende a +inf mentre per x->-inf  la funzione tende a zero; la funzione cresce per x>-1 e decresce per x<-1; presenta una concavità verso l'alto per x>-2 e verso il basso per x<-2. Naturalmente avremo un minimo relativo in x=-1 e un flesso in x=-2

y=(e^x)/(e^x +1)

1)La funzione è definita per ogni x appartenente ad R

2)E' una funzione sempre positiva

3)Interseca l'asse x nel punto Y=1/2

4)Per x->+inf la funzione tende a 1; mentre per x->-inf la funzione tende a 0

5)E' una funzione sempre crescente; non esistono massimi e minimi

6)Presenta una concavità verso l'alto per x<0 e concavità verso il basso per x>0; flesso in x=0

Legenda:

-> =tende    R =numeri reali    inf =infinito e =numero di Nepero