|
|
| |
Il lavoro di Galois
Galois, all'inizio del suo lavoro, indirizzò i suoi studi nella ricerca di una formula risolutiva per le equazioni di grado superiore al quarto, ignorando che un suo contemporaneo norvegese, Abel, nel frattempo aveva dimostrato che ciò era impossibile.
Nel corso delle sue ricerche Galois scoprì un ramo della matematica fino ad allora sconosciuto: l'Algebra astratta.
Un'operazione binaria è una corrispondenza univoca tra il prodotto cartesiano tra NxN e N stesso,
Es.: NxN N
Da precisare che un'operazione binaria è un'operazione fra due numeri,
Es.: 2+3=5;
inoltre si intende per prodotto cartesiano l'insieme di tutte le coppie ordinate di un prodotto fra insiemi.
Es.: A=, quindi le coppie ordinate sono:
Se il risultato del prodotto di una coppia di insiemi dà per risultato un elemento dello stesso insieme, allora esso si dice "interno".
Facendo un'operazione tra insiemi se il risultato è interno allora è una struttura algebrica.
Es.: A°, ogni prodotto eseguito fra elementi dell'insieme dà per risultato un elemento dello stesso insieme, quindi si può dire che è un'operazione interna.
Se la struttura algebrica possiede la proprietà associativa diventa un semigruppo.
Es.: A. se facciamo (1.1). -1= -1, ma se associamo due numeri consecutivi in modo diverso e il risultato è uguale gode della proprietà associativa, 1.(1.-1)= -1.
Se all'intero di un semigruppo c'è un elemento neutro, cioè un elemento che operato con un altro dà per risultato l'altro, e nel semigruppo ogni elemento ha il suo inverso, cioè un elemento che operato col primo dà per risultato un elemento neutro, allora l'insieme prende il nome di Gruppo.
Inoltre, quando un gruppo gode della proprietà commutativa viene detto Gruppo

Con le operazioni tra insiemi è possibile costruire delle tabelle.
Ad esempio, l'insieme X= * (supponendo che * e un segno qualunque)
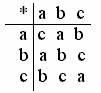
Questa tabella è un gruppo Abeliano perché:
per essere un gruppo gli elementi devono trovarsi una sola volta in ogni riga e in ogni colonna;
l'elemento neutro si trova in corrispondenza della riga e della colonna dove gli elementi sono disposti nell'ordine iniziale;
se in una tabella la diagonale che parte dal segno è un asse di simmetria tra gli elementi non intersecati da questa allora il gruppo gode della proprietà commutativa.
Classi resto
Le classi resto sono degli insiemi ottenuti dividendo dei numeri per un modulo, ad esempio le
classi resto mod. 3 sono tutti i resti ottenuti dividendo dei numeri per tre, queste classi quindi saranno 0, 1, 2.
Con le classi resto è possibile fare delle operazioni, prendiamo per esempio una somma tra le classi resto mod. 3 (il segno della somma è o
![]()
![]()
![]()
2 o perché 2+2=4 e siccome 4 è nella classe di resto 1 il risultato è 1.
La somma tra le classi resto mod. 3 si può sintetizzare nella seguente tabella:
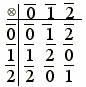
Anche questa tabella è un gruppo Abeliano perché corrisponde ai canoni descritti precedentemente.
Insiemi con le trasformazioni geometriche
prendiamo come insieme T, dove I è un triangolo equilatero di vertici A, B, C ; R e la rotazione di I di 120° ed R² è la rotazione di I di 240°:
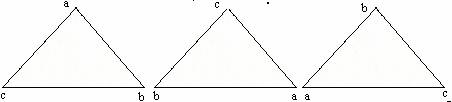
I R R²
Facendo il prodotto fra T e T, ne risulta la seguente tabella:
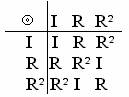
anche questa tabella è un gruppo Abeliano.
La stessa cosa si può fare con altre figure e altre trasformazioni geometriche, ad esempio con la rotazione dei quadrati:
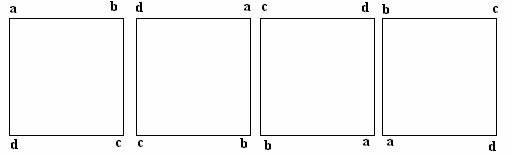
I R R² R³
Da T= risulterà la seguente tabella:
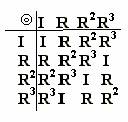
la quale è un gruppo Abeliano.
Per quanto riguarda altre trasformazioni geometriche prendiamo in esame, oltre alla rotazione, le simmetrie rispetto all'altezza nel triangolo equilatero:
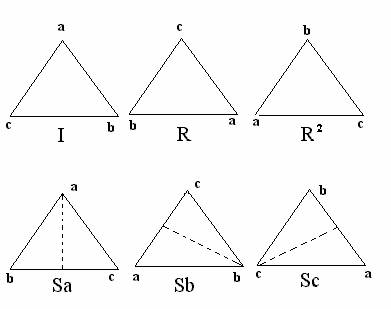
Dall'insieme Ts = si ricava la seguente tabella, che rappresenta un gruppo Abeliano:

Le permutazioni
Supponiamo che volendo sistemare tre persone attorno a un tavolo rotondo dobbiamo calcolare tutte le combinazioni possibili(scrivendole tra parentesi assieme all'ordine standard):
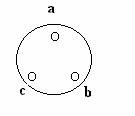
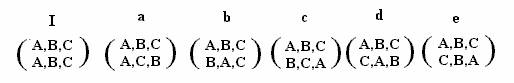
la tabella sarà la seguente:
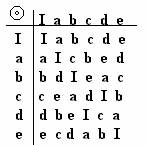
Questa tabella ha molte analogie con quella precedentemente descritta (T=),
infatti se poniamo: I=I, R=d, R²=c, Sa=a, Sb=b, Sc=c, le tabelle sono molto simili:

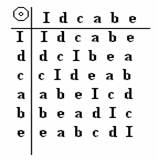
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025