DISTANZA DI DUE PUNTI NEL PIANO CARTESIANO

matematica

• DISTANZA DI DUE PUNTI NEL PIANO CARTESIANO

• COORDINATE DEL PUNTO MEDIO TRA DUE PUNTI

• COORDINATE DEL BARICENTRO DI UN TRIANGOLO

• EQUAZIONE DI UNA RETTA PASSANTE PER DUE PUNTI

• EQUAZIONE DI UNA RETTA ASSEGNATO UN PUNTO ED IL COIFFICIENTE ANGOLARE

• COIFFICIENTE ANGOLARE ASSEGNATI DUE PUNTI

• DISTANZA DI UN PUNTO DA UNA RETTA

• ANGOLO TRA DUE RETTE

• STUDIO DEL DISCRIMINANTE 818c21i

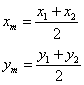
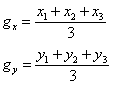
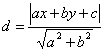
D > 0

a concorde con il segno della funzione Valori esterni

a discorde con il segno della funzione Valori interni

D < 0

a concorde con il segno della funzione Tutti i valori

a discorde con il segno della funzione Nessun Valore

D

a concorde con il segno della funzione Tutti i valori tranne x1 e x2

a discorde con il segno della funzione Nessun Valore

• TEOREMI DI EUCLIDE

I° Teorema:

• TEOREMI DELLE CORDE E DELLE SECANTI

• FORMULA DI ERONE

• TEOREMA DI CARNOT

• SOMMA DI DUE VETTORI PARALLELI

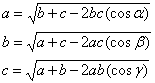
La somma di R1 avviene con l'opposto R2.

La diagonale R3 del parallelogramma è la risultante

• PRODOTTO SCALARE DI DUE VETTORI

			Il prodotto avviene tra il vettore e la proiezione di , su ,

  

Equazione della circonferenza

con

Si ha:

CENTRO DELLA CIRCONFERENZA

 

RAGGIO DELLA CIRCONFERENZA

IN EQUAZIONE PER RAPPRESENTARE UNA CIRCONFERENZA DEVE ESSERE:

PUNTI DI INTERSEZIONE

X determinare punti intersezione di retta con circonferenza a sistema equazioni date. Sostituendo avrai equazione di secondo grado. Risolvila avrai due valori. Sostituendoli all'equazione della retta si avranno le quattro coordinate.

RETTA TANGENZTE AD UNA CIRCONFERENZA

1) Scrivi equazione generica retta per P e determini coefficiente angolare ponendo distanza dal centro circonferenza = a r. Calcoli retta sapendo coefficiente e punto.

2) Metti a sistema equazione generica a circonferenza. Con sostituzione elimini incognita e ottieni coefficienti con m. Calcolare il D di D e trovi coefficienti. Calcoli rette sapendo coefficienti e punto.