ESERCIZIO - METODO PARAMETRICO

matematica

ESERCIZIO 1

Si supponga di utilizzare due diversi test psicologici per la valutazione di un gruppo di 9 pazienti con problemi depressivi. I risultati sono riportati nella seguente tabella:

Verificare se esiste una correlazione tra i risultati dei due test sia con metodo parametrico che con metodo non parametrico.

Si vuole verificare se c'è una correlazione lineare tra tra i risultati dei due diversi test psicologici (variabili).

METODO PARAMETRICO

v DATI

Si dispone dei risultati di due diversi test psicologici effettuati su un gruppo di 9 pazienti con problemi depressivi.

v ASSUNZIONI

o   Le variabili X e Y seguono una distribuzione normale bivariata

La misura della forza di associazione tra le due variabili X (test 1) e Y (test 2) è data dal coefficiente di correlazione di Pearson:

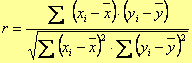
Con -1 r

La formula utilizzata per i calcoli è:

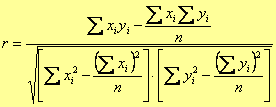
Per rendere i calcoli più agevoli si utilizza la tabella:

Quindi

Il valore di r è comunque una stima campionaria del valore del coefficiente di correlazione r della popolazione. Bisogna ora verificare se il valore di r ottenuto è significativo.

v IPOTESI

H₀: r

H_i : r

v STATISTICA TEST

v DISTRIBUZIONE DELLA STATISTICA TEST

Distribuzione t-Student caratterizzata da n-2 gradi di libertà.

v REGOLA DI DECISIONE

Conoscendo la distribuzione della statistica test a 7 gradi di libertà e un livello di significatività a=0,05, ricerco il valore di t tabulato:

t_tab =  2,365

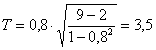
Quindi:

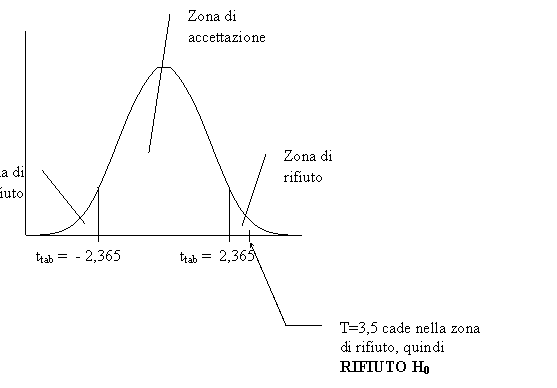
DECISIONE DEL RICERCATORE:

Non esiste una correlazione tra i due test psicologici.

METODO NON PARAMETRICO

v DATI

v ASSUNZIONI

o   Non è possibile fare assunzioni sulla distribuzione delle due variabili.

Il coefficiente di correlazione da usare è quello di Spearman:

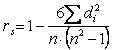
Dove d_i sono le differenze dei ranghi attribuiti ai valori delle due variabili.

v IPOTESI

H₀: r = 0 (le due variabili non sono correlate)

H_i : r

v REGOLA DI DECISIONE

La decisione verrà presa confrontando il vaolre di r_s calcolato con il valore di r_s tabulato sulle tavole di Spearman, in corrispondenza del livello di significatività del test (a=0,05) e del numero di coppie di osservazioni delle due variabili (9 coppie).

Se r_s  calc > r_s tab rifiuto H₀.

r_s calc = 0,8

r_s  tab = 0,683

essendo r_s calc > r_s tab, rifiuto H₀

DECISIONE DEL RICERCATORE

Non esiste una correlazione tra i due test psicologici.

ESERCIZIO 2

Si dispone dei valori del volume diastolico, misurato in ml, di 10 pazienti cardiopatici rilevati mediante angiografia (X) e scintigrafia (Y):

Verificare il grado di associazione tra le due variabili sia con il metodo parametrico che con il metodo non parametrico.

Si vuole verificare quanto le variabili X e Y siano associate, cioè se c'è correlazione tra il volume diastolico misurato mediante angiografia, e il volume diastolico misurato mediante scintigrafia in 10 pazienti cardiopatici.

METODO PARAMETRICO

v DATI

Si dispone dei valori di volume diastolico, misurato in ml, mediante angiografia (X) e scintigrafia (Y), di 10 pazienti cardiopatici:

v ASSUNZIONI

o   Le variabili X e Y seguono una distribuzione normale bivariata

La misura della forza di associazione tra le due variabili X (test 1) e Y (test 2) è data dal coefficiente di correlazione di Pearson:

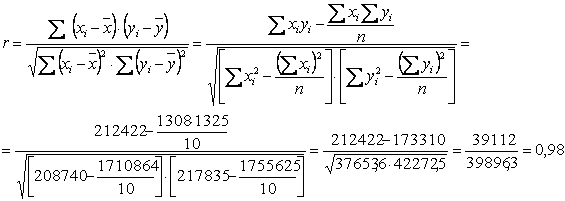
Il valore di r è una stima campionaria del valore del coefficiente di correlazione r della popolazione. Bisogna ora verificare se il valore di r ottenuto è significativo.

v IPOTESI

H₀: r

H_i : r

v STATISTICA TEST

v DISTRIBUZIONE DELLA STATISTICA TEST

Distribuzione t-Student caratterizzata da n-2 gradi di libertà.

v REGOLA DI DECISIONE

Conoscendo la distribuzione della statistica test a 8 gradi di libertà e un livello di significatività a=0,05, ricerco il valore di t tabulato:

t_tab =  2,306

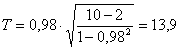
Quindi:

DECISIONE DEL RICERCATORE:

Non esiste una correlazione tra i due metodi.

METODO NON PARAMETRICO

v DATI

v ASSUNZIONI

o   Non è possibile fare assunzioni sulla distribuzione delle due variabili.

Il coefficiente di correlazione da usare è quello di Spearman:

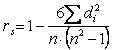
Dove d_i sono le differenze dei ranghi attribuiti ai valori delle due variabili.

v IPOTESI

H₀: r = 0 (le due variabili non sono correlate)

H_i : r

v REGOLA DI DECISIONE

La decisione verrà presa confrontando il valore di r_s calcolato con il valore di r_s tabulato sulle tavole di Spearman, in corrispondenza del livello di significatività del test (a=0,05) e del numero di coppie di osservazioni delle due variabili (10 coppie).

Se r_s calc > r_s  tab rifiuto H₀.

r_s calc = 0,96

r_s  tab = 0,648

essendo r_s calc > r_s tab, rifiuto H₀

DECISIONE DEL RICERCATORE

Non esiste una correlazione tra le due misurazioni.

ESERCIZIO 3

Utilizzando i dati in tabella relativi ad un campione di donne classificate secondo gli stadi dell'infezione da HIV e la presenza di papilloma HPV:

Valutare se la percentuale di donne positive ad HPV è la stessa oppure no nei diversi stadi di infezione da HIV. Limitando l'attenzione alle donne positive sintomatiche e positive asintomatiche, verificare se la presenza di HPV è ugualmente probabile nei due gruppi con tutti i metodi noti.

A)    Si vuole valutare se la percentuale di donne positive ad HPV è la stessa oppure no nei diversi stadi di infezione da HIV, cioè se l'essere HPV positive è correlato all'essere HIV positive.

v ASSUNZIONI

o   Le variabili di cui disponiamo sono qualitative

o   Se consideriamo una sola cella, la presenza contemporanea delle due caratteristiche è il "successo", sugli N casi possibili: si può assumere una distribuzione binomiale

o   I dati nel loro insieme seguono una distribuzione mulrinomiale.

v IPOTESI

H₀: p_ij = p_i p_j (equivale a dire che HPV e HIV sono correlati

e quindi la percentuale di donne positive ad HPV è la stessa

nei diversi stadi di infezione da HIV)

H₁: p_ij p_i p_j

se le due variabili sono indipendenti la probabilità di avere la caratteristica 1 e la caratteristica 2 sarà data dal prodotto delle probabilità (legge del prodotto).

I VALORI ATTESI

È possibile calcolare il valore atteso Eij ("media") per ciascuna cella:

E_ij = Np_ij = Np_ip_j = N(n_.j/N)(n_i./N) = (n_.j n_i.)/N

Si può costruire quindi la tabella dei valori attesi:

v STATISTICA TEST

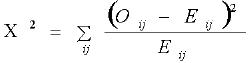
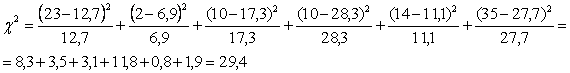
v DISTRIBUZIONE DELLA STATISTICA TEST

La distribuzione della statistica test è una c² ed è caratterizzata dai gradi di libertà:

v REGOLA DI DECISIONE

Fissato a accettabilmente piccolo (0,05), troverò sulle tavole c² un valore in corrispondenza di a prescelto e dei gradi di libertà della statistica.

g.l.= (r-1)(c-1) =(2-1)(3-1)=2  c _{a=0,05; gl 2}

DECISIONE STATISTICA

5,99 < 29,4 rifiuto l'ipotesi nulla, ovvero le due variabili sono indipendenti

DECISIONE DEL RICERCATORE

La percentuale di donne positive ad HPV non è la stessa nei diversi stadi di infezione da HIV.

B) Si vuole verificare se la percentuale di donne positive ad HPV è la stessa oppure no nei diversi stadi di infezione da HIV.

METODO PARAMETRICO

v DATI

v ASSUNZIONI

o   campioni indipendenti;

o   la variabile in studio che conta il numero di donne HIV e HPV positive asintomatiche o sintomatiche ("successo") sul totale (numerosità del campione) segue una distribuzione binomiale;

o   la distribuzione della variabile è approssimabile ad una distribuzione di Gauss standard se n e p

v IPOTESI

H₀: p₁=p₂ oppure p₁-p₂=0

H₁: p₁ p₂

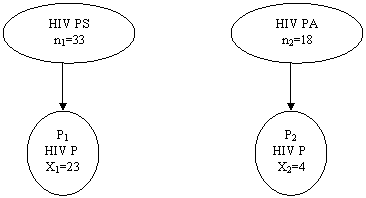
v STATISTICA TEST

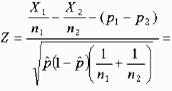
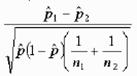
Dove:

p=(X₁+X₂)/(n₁+n₂)

q=1-p

p₁=X₁/n₁

p₂=X₂/n₂

p=(23+4)/(37+37)=0,4

q=1-p=0,6

p₁=23/37=0,6

p₂=4/37=0,1

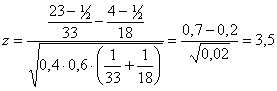
v DISTRIBUZIONE DELLA STATISTICA TEST

Con l'ipotesi nulla vera, applicando il teorema del limite centrale, la statistica test segue una distribuzione di Gauss standard N(0,1).

Fissato a, la probabilità di rifiutare l'ipotesi nulla quando è vera, accettabilmente bassa: 0,05, si individuano della zona di rifiuto (code).

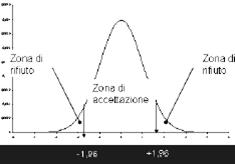
DECISIONE STATISTICA

Z_cal=3,5 > Z_tab=1,96 pertanto rifiuto H₀

DECISIONE DEL RICERCATORE

La presenza di HPV è ugualmente probabile nei due gruppi.

METODO NON PARAMETRICO

Non è possibile approssimare la distribuzione binomiale ad una Gauss standard, quindi il confronto tra le due proporzioni se effettua con il test del c

I dati si inseriscono in una tabella 2

IPOTESI

H₀: p₁=p₂

H₁: p₁ p₂

STATISTICA TEST

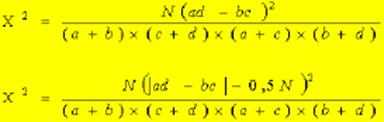
Distribuzione della statistica test

La distribuzione della statistica test è una c² ed è caratterizzata dai gradi di libertà:

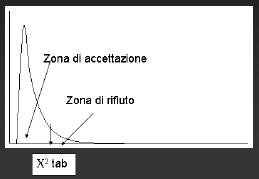
REGOLA DI DECISIONE

Con a=0,05 e g.l=(r-1)(c-1)=1, il valore c² tabulato è 3,841.

DECISIONE STATISTICA

Rifiuto l'ipotesi nulla poiché il valore di c² _calc è 8,7 > c²_tab

DECISIONE DEL RICERCATORE

La presenza di HPV è ugualmente probabile nei due gruppi.

ESERCIZIO 4

Un gruppo di 500 pazienti psichiatrici è stato classificato secondo il tipo di reazione ricorrente e la terapia scelta per la cura:

Valutare l'esistenza di una associazione tra il tipo di reazione e la terapia.

Si vuole verificare se vi è una correlazione tra il tipo di reazione ricorrente e la terapia scelta per la cura.

v DATI

v ASSUNZIONI

o   Le variabili di cui disponiamo sono qualitative

o   Se consideriamo una sola cella, la presenza contemporanea delle due caratteristiche è il "successo", sugli N casi possibili: si può assumere una distribuzione binomiale

o   I dati nel loro insieme seguono una distribuzione mulrinomiale.

v IPOTESI

			pij = Oij / N pi = ni / N pj = nj / N

H₀: p_ij = p_i p_j

H₁: p_ij p_i p_j

se le due variabili sono indipendenti la probabilità di avere la caratteristica 1 e la caratteristica 2 sarà data dal prodotto delle probabilità (legge del prodotto).

I VALORI ATTESI

È possibile calcolare il valore atteso Eij per ciascuna cella:

E_ij = Np_ij = Np_ip_j = N(n_.j/N)(n_i./N) = (n_.j n_i.)/N

Si può costruire quindi la tabella dei valori attesi:

v STATISTICA TEST

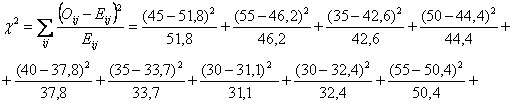
v DISTRIBUZIONE DELLA STATISTICA TEST

La statistica test è  ed è caratterizzata da (r - 1)(c - 1) = 6 gradi di libertà.

v REGOLA DI DECISIONE

Con a=0,05 e g.l=(r-1)(c-1)=6, il valore c² tabulato è 14,7.

DECISIONE STATISTICA

Accettto l'ipotesi nulla poiché il valore di c² _calc = 5,6 è <  c²_tab

DECISIONE DEL RICERCATORE

Non vi è una associazione tra il tipo di reazione e la terapia.

ESERCIZIO 5

Un gruppo di 300 pazienti neoplastici è stato classificato secondo la sede del tumore e la professione:

Valutare l'esistenza di una associazione tra il tipo di tumore e la professione.

Si vuole verificare se vi è una correlazione tra il tipo di tumore e la professione.

v DATI

v ASSUNZIONI

o   Le variabili di cui disponiamo sono qualitative

o   Se consideriamo una sola cella, la presenza contemporanea delle due caratteristiche è il "successo", sugli N casi possibili: si può assumere una distribuzione binomiale

o   I dati nel loro insieme seguono una distribuzione multinomiale.

v IPOTESI

			pij = Oij / N pi = ni / N pj = nj / N

H₀: p_ij = p_i p_j

H₁: p_ij p_i p_j

se le due variabili sono indipendenti la probabilità di avere la caratteristica 1 e la caratteristica 2 sarà data dal prodotto delle probabilità (legge del prodotto).

I VALORI ATTESI

È possibile calcolare il valore atteso Eij per ciascuna cella:

E_ij = Np_ij = Np_ip_j = N(n_.j/N)(n_i./N) = (n_.j n_i.)/N

Si può costruire quindi la tabella dei valori attesi:

v STATISTICA TEST

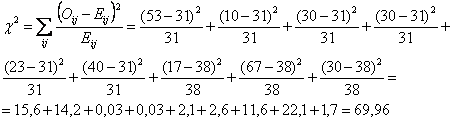
v DISTRIBUZIONE DELLA STATISTICA TEST

La statistica test è  ed è caratterizzata da (r - 1)(c - 1) = 4 gradi di libertà.

v REGOLA DI DECISIONE

Con a=0,05 e g.l=(r-1)(c-1)=4, il valore c² tabulato è 9,49.

DECISIONE STATISTICA

Rifiuto l'ipotesi nulla poiché il valore di c² _calc = 69,96 è >  c²_tab

DECISIONE DEL RICERCATORE

Non vi è una correlazione tra il tipo di tumore e la professione.