EQUAZIONE DELLA RETTA (Nel Piano Cartesiano) [GEOMETRIA ANALITICA]

matematica

EQUAZIONE DELLA RETTA (Nel Piano Cartesiano)

[GEOMETRIA ANALITICA]

La Retta, rappresentata sul piano cartesiano, come argomento di Geometria analitica.

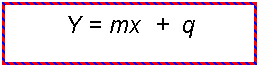Una retta č definita, nel piano cartesiano, dall'equazione: 

Si definisce fun 252e46c zione y della variabile x un legame fra due variabili, una detta variabile indipendente x e l'altra detta variabile dipendente y tali che abbiano senso le operazioni da effettuare sulla x per ottenere i valori della y e per ogni valore della x corrisponda un solo valore della y. (Se inserisco un valore arbitrario di X mi arriva un determinato valore Y.)

y=f(x)

Possiamo dunque dire che la retta č una funzione.

y = mx + q

	Termine noto (translazione)
					Sono sempre dei numeri (anche 0) (anche

Coefficiente angolare (pendenza)

)

9