|
|
| |
AFFINITA
DEFINIZIONE: trasformazione che trasforma rette in rette
generica equazione:
![]()
![]()
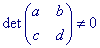
PROPRIETÀ: 747c22h
se ![]() la trasformazione è diretta
la trasformazione è diretta
se ![]() la trasformazione è invertente
la trasformazione è invertente
mantiene il parallelismo (a rette parallele corrispondono rette parallele)
conserva il rapporto tra segmenti paralleli
se la figura ![]() è trasformata della
figura
è trasformata della
figura ![]() allora
allora ![]()
NELLO STUDIO DI SIMMETRIE RISPETTO A RETTE PER O
SONO A VOLTE UTILI LE FORMULE PARAMETRICHE:
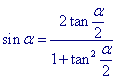
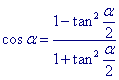
ESEMPIO:
simmetria rispetto a ![]() quindi
quindi ![]()
![]()
![]()
NB: LE AFFINITÀ CHE NON SONO NÉ ISOMETRIE
NÉ SIMILITUDINI SI DICONO AFFINITÀ GENERICHE;
TRA QUESTE CI SONO LE DILATAZIONI:
![]()
ISOMETRIA DIRETTA:
generica equazione:
![]()
![]()
![]()
ROTAZIONE DI CENTRO O (ORIGINE DEGLI ASSI):
generica equazione:
![]()
![]()
![]()
ISOMETRIA INVERTENTE:
generica equazione:
![]()
![]()
![]()
SIMMETRIA
RISPETTO A UNA RETTA PER O (![]() ):
):
generica equazione:
![]()
![]()
![]()
NELLA SCRITTURA
NORMALE TROVIAMO ![]() AL POSTO DI
AL POSTO DI ![]()
OMOTETIA DI CENTRO O:
generica equazione:
![]()
![]()
![]()
SIMILITUDINE:
UNA
SIMILITUDINE SI PUÒ VEDERE COME
QUINDI
SIMILITUDINE DIRETTA
![]()
![]()
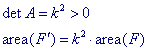
QUINDI:
![]()
![]()
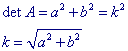
SIMILITUDINE INVERTENTE
![]()
![]()
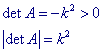
QUINDI:
![]()
![]()
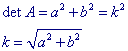
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025