|
|
| |
Schema riassuntivo: I PASSI PER LO STUDIO DEL GRAFICO DI UNA FUNZIONE
0) &n 444f59e bsp; Può darsi che il grafico della funzione f da studiare si possa ricavare con "manipolazioni" &n 444f59e bsp; a partire dal grafico (già noto o comunque molto più facile da tracciare) di una funz. più semplice g.
&n 444f59e bsp; &n 444f59e bsp; Ad esempio, ciò avviene se f è della forma
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
&n 444f59e bsp; &n 444f59e bsp; &n 444f59e bsp; Bisogna comunque valutare se valga la pena di impostare un lavoro di questo tipo, tenendo conto della difficoltà delle manipolazioni; a volte, questo approccio "dà subito un'idea" - utilissima - dell'andamento della f, ricavato da quello della g, ma per la determinazione dei massimi, minimi ecc. sarà poi necessario ricorrere alle tecniche esposte ai punti successivi di questo schema.
1) &n 444f59e bsp; &n 444f59e bsp; Determinare il dominio D della funzione
2) &n 444f59e bsp; &n 444f59e bsp; Chiedersi se la funzione
&n 444f59e bsp; è pari:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() &n 444f59e bsp;e quindi ha
grafico simmetrico rispetto all'asse y
&n 444f59e bsp;e quindi ha
grafico simmetrico rispetto all'asse y
&n 444f59e bsp;
dispari: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e quindi ha
grafico simmetrico rispetto all' origine
e quindi ha
grafico simmetrico rispetto all' origine
&n 444f59e bsp; oppure né pari né dispari
&n 444f59e bsp; &n 444f59e bsp;
Nel caso la funzione
sia pari o dispari, nelle varie fasi dello studio potremo e dovremo tenere
presente la simmetria riscontrata; potremmo addirittura decidere di studiare la
funzione soltanto per ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() e
poi completarne il grafico per simmetria (la convenienza di procedere in questo
modo dipende dalle nostre preferenze, e dalla particolare funzione di volta in
volta considerata).
e
poi completarne il grafico per simmetria (la convenienza di procedere in questo
modo dipende dalle nostre preferenze, e dalla particolare funzione di volta in
volta considerata).
Chiedersi se la funzione è periodica
in caso affermativo, basterà studiarla su di un intervallo di ampiezza T (essendo T il periodo).
&n 444f59e bsp; &n 444f59e bsp;
Ricordare
comunque che, se ad es. si lavora sull'intervallo ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
sarà sempre conveniente, nei vari schemi, andare anche "leggermente a
sinistra di 0" e "leggermente a destra di
,
sarà sempre conveniente, nei vari schemi, andare anche "leggermente a
sinistra di 0" e "leggermente a destra di ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() "
"
3) &n 444f59e bsp; Determinare le intersezioni con gli assi
&n 444f59e bsp; Per l'eventuale intersezione con l'asse verticale si porrà x=0 (se, beninteso, l'ascissa 0 appartiene al dominio!) e si ricaverà il corrispondente valore di y
&n 444f59e bsp; Per le eventuali intersezioni con l'asse orizzontale si dovrà risolvere l'equazione f(x) = 0.
4) &n 444f59e bsp; &n 444f59e bsp; Studiare il segno della funzione mediante la disequazione f(x) > 0.
&n 444f59e bsp; &n 444f59e bsp; Ricordare che, se la risoluzione di tale disequazione comporta l'utilizzo di uno schema, in tale schema converrà riportare anche gli eventuali confini finiti del dominio, ed eliminare subito, sbarrandole, le "parti dell'asse x dove la funzione non esiste".
5) &n 444f59e bsp; &n 444f59e bsp; Calcolare i limiti ai confini del dominio
&n 444f59e bsp; &n 444f59e bsp; Così facendo si troveranno anche, se esistono, gli asintoti verticali ed orizzontali
&n 444f59e bsp; &n 444f59e bsp; A volte (caso poco frequente), il dominio non ha un'interruzione nell'ascissa c, tuttavia si riscontra che la funzione è discontinua in c. E' chiaro che converrà allora chiedersi cosa accade alla f(x) quando x tende a c, da sinistra e da destra. Può darsi fra l'altro che, in questo modo, si trovi un altro asintoto verticale.
&n 444f59e bsp; &n 444f59e bsp; Osserviamo che, evidentemente, avrà senso ricercare un eventuale asintoto obliquo per la funzione y = f(x) soltanto se si è constatato che la funzione tende a infinito quando x tende a infinito.
&n 444f59e bsp; &n 444f59e bsp; Ricordiamo ancora il Teorema sul quale si basa il procedimento di ricerca degli eventuali asintoti obliqui.
a) &n 444f59e bsp;
esiste
finito e diverso da zero il 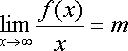
![]()
![]()
![]()
![]()
![]()
![]()
![]() &n 444f59e bsp; &n 444f59e bsp; b)
esiste finito il
&n 444f59e bsp; &n 444f59e bsp; b)
esiste finito il ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ricercare (utilissimo!) le eventuali intersez. del grafico con gli asintoti (obliqui od orizzontali)
6) &n 444f59e bsp; Calcolare la derivata prima y' = f ' (x). Poi:
a) &n 444f59e bsp;
&n 444f59e bsp; &n 444f59e bsp; Determinare il dominio D' della y '
Tale dominio D' potrebbe essere più ristretto del dominio D della funzione ; ciò significherebbe che in certi punti la funzione esiste, ma non è derivabile.
Eventuali punti di questo tipo sono sempre interessanti! Si potrà trattare di: flessi verticali, cuspidi, punti angolosi.
&n 444f59e bsp; &n 444f59e bsp; Calcolare i limiti della y' quando x tende ai confini di D'
Da questi limiti si trarranno sempre indicazioni utili sull'andamento della funzione;
inoltre, se D' è più ristretto di D, si chiarirà in questo modo la natura dei punti in cui la y esiste ma non è derivabile.
b) &n 444f59e bsp; Risolvere l'equazione f ' (x) = 0 per trovare i cosiddetti "punti stazionari"
( = punti in cui il grafico ha tangente orizzontale).
c) &n 444f59e bsp; Studiare il segno della derivata prima con la disequazione f ' (x) > 0
stabilendo così gli intervalli in cui la funzione è
|
&n 444f59e bsp; &n 444f59e bsp; crescente y ' > 0 implica retta tangente in salita, funzione crescente &n 444f59e bsp; &n 444f59e bsp; decrescente ( y ' < 0 implica retta tang. in discesa, funz. decrescente |
|
e determinando i punti di massimo relativo e minimo relativo interni al dominio,
nonché i punti di flesso orizzontale (ascendente o discendente).
Se la risoluzione di tale disequaz. comporta l'utilizzo di uno schema, in tale schema converrà riportare anche gli eventuali confini finiti del dominio D' della derivata prima, chiedendosi "cosa succede" in corrispondenza di questi estremi:
&n 444f59e bsp; la derivata prima "diventa infinita"?
&n 444f59e bsp; la derivata prima "non esiste perchè derivata sinistra e destra sono distinte" (punto angoloso)?
&n 444f59e bsp; la derivata prima...
A volte la risoluzione della disequazione f ' (x) > 0 è troppo complicata. In tal caso, si può valutare se sia il caso di rinunciare a tale disequazione. Ricordiamo poi che, per l'analisi dei punti stazionari, esiste anche la risorsa del "metodo della derivata seconda o delle derivate successive"
&n 444f59e bsp; &n 444f59e bsp; Calcolare la derivata seconda y''= f '' (x).
Risolvere l'equazione f '' (x) = 0.
Quest'ultima fornisce, in generale, le ascisse dei punti di flesso; ricordiamo però che
&n 444f59e bsp; non tutti i punti in cui si annulla la y" risultano poi di flesso;
&n 444f59e bsp; e, d'altra parte (caso non frequentissimo, ma possibile: basti pensare ai flessi verticali),
si possono avere pure dei flessi in cui la y'' non si annulla.
Studiare il segno della derivata seconda, mediante la disequazione f '' (x) > 0.
Tale studio permetterà di stabilire gli intervalli in cui la funzione è concava e quelli in cui è convessa:
|
|
Ciò darà indicazioni utili sull'andamento della funzione e consentirà:
&n 444f59e bsp; di chiarire la natura di quei punti nei quali si annulla la derivata seconda
(questi possono essere di flesso, ma anche non esserlo);
&n 444f59e bsp; di determinare eventuali punti che risultano di flesso anche senza che in essi si annulli la y''
&n 444f59e bsp; &n 444f59e bsp; Se la risoluzione della disequazione f '' (x) > 0 comporta l'utilizzo di uno schema, in tale schema converrà riportare anche gli eventuali confini finiti del dominio D'' della derivata seconda, chiedendosi "cosa succede" alla y'' quando x tende a ciascuno di questi estremi.
&n 444f59e bsp; &n 444f59e bsp; A volte la risoluzione della disequazione f '' (x) > 0 è troppo complicata. In tal caso, si può valutare se rinunciare a tale disequazione.
Può talvolta essere conveniente, per la ricerca dei flessi non orizzontali, il "metodo delle derivate successive"
|
In corrispondenza dei punti di flesso a tangente non orizzontale, converrà calcolare il valore della derivata prima, per avere il coeff. ang. della tangente di flesso, e disegnare nel grafico "un pezzetto" di tale tangente di flesso, con l'inclinazione esatta, segnando accanto ad essa &n 444f59e bsp; il valore del suo coefficiente angolare m |
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025