PROGRAMMA DI MATEMATICA - INTEGRALI INDEFINITI

Chiamiamo integrale indefinito di f (x) questa primitiva generale e lo rappresentiamo con il seguente simbolo:

∫ f (x) dx

Utilizzando il "dx " la scrittura indica che la derivata avviene rispetto alla variabile x e contiene in sé la costante C. La f (x) prende nome di funzione integranda e avremo quindi:

∫ f (x) dx = F (x) + C F' (x) = f (x)

L'integrale indefinito di f (x) è la totalità delle primitive di f (x), cioè l'insieme di tutte e solo le funzioni la cui derivata è f (x), e può essere considerato come operatore inverso della derivata.

ESEMPI-------- ----- ------ -------- ----- ------ -------- ----- ------ ----------

∫ 3 x ² dx = x ³ + C

Ricordano le regole di derivazione sappiamo che la derivata di una potenza è :

D ( x ⁿ ) = n x ^{( n - 1 )}

Perciò l'integrale di " n x ^{( n - 1 )} " ha come risultato " x ⁿ + C " .

PROPRIETA' INTEGRALI INDEFINITI-------- ----- ------ -------- ----- ------

Una costante moltiplicativa si può trasportare dentro o fuori del segno di integrale:

∫ k f (x) dx = k ∫ f (x) dx

L'integrale della somma algebrica (o sottrazione) di due o più funzioni è uguale alla somma ( o

sottrazione) degli integrali delle singole funzioni:

∫ ( f1 (x) + f2 (x) ) dx = ∫ f1 (x) dx + ∫ f2 (x) dx

L'integrale indefinito, se gode di queste due proprietà, è detto operatore lineare.

INTEGRAZIONI IMMEDIATE-------- ----- ------ -------- ----- ------ ------------

Per integrazione di una funzione si intendono le procedure di calcolo necessarie per ottenere le primitive. Se la funzione integranda f (x) è la derivata di una funzione nota, l'integrazione è immediata.

Esempi di integrazioni immediate:

∫ dx x + c

∫ k dx k x + c ∫ 2 dx 2 x + c

∫ x dx ½ x ² + c ∫ x ² dx ⅓ x ³ + c

∫ x n dx x ^{n + 1} + c

n + 1

∫ 1 dx log |x| + c

x

∫ sen x dx - cos x + c

∫ cos x dx sen x + c

∫ √x dx ∫ x ^½ dx x ^{½ + 1} + c x ^3⁄2 + c ⅔ √ x ³ + c ⅔ x √ x + c

½ + 1 ³⁄₂

∫ 1 dx ∫ x ^-½ dx x ^{-½ + 1} + c x ^1⁄2 + c 2 √ x + c

√x - ½ + 1 ¹⁄₂

∫ e^x dx e^x + c

∫ e^2x dx 2 ∫ e^2x dx 1 ∫ 2 e^x dx 1 e ^2x + c

2 2 2

∫ a^x dx a^x + c

log a

1 dx arc sen x + c

√ 1 - x ²

1 dx arc sen x + c

√ a² - x ² a

∫ 1 dx arc tg x + c

√ 1 + x ²

∫ f ' (x) dx log x + c

f (x)

INTEGRAZIONE DELLE FUNZIONI RAZIONALI FRATTE-------- ----- ------ ------

∫ px + q dx

ax² + bx + c

Per integrare una funzione razionale fratta occorre distinguere due casi principali:

quando il grado del numeratore è maggiore del grado del denominatore;

quando il grado del denominatore è maggiore del grado del numeratore.

Nel primo caso il modo più semplice per integrare la funzione è fare la divisione tra numeratore e denominatore come nell'esempio:

∫ 4 x² + x - 1 dx =

x - 3

4 x² + x - 1 x - 3

- 4 x² + 12 x

4 x + 13

+ 13 x - 1

- 13 x + 39

+ 38

∫ 4 x + 13 + 38 dx ∫ 4 x dx + ∫ 13 dx + ∫ 38 dx 2 x² + 13 x + 38 log |x - 3| + C

x - 3 x - 3

Nel secondo caso, invece, si analizza il comportamento del denominatore e quindi si risale a tre possibili casi :

Δ > 0

Δ = 0

Δ < 0

Primo caso Δ > 0 :

Il polinomio al denominatore della funzione razionale fratta in questo caso è scomponibile in fattori: dette x1 e x2 le sue soluzioni, sappiamo che ax² + bx + c = a ( x - x1) ( x - x2).

La funzione integranda si può quindi scomporre nella somma di due frazioni :

A + B .

x - x1 x - x2

facilmente integrabile. Le costanti A e B si determinano applicando il principio di identità dei polinomi, come nell'esempio:

Calcolare ∫ 2x - 7 dx =

x² - x - 2

per il trinomio x² - x - 2 è Δ = 1 + 8 > 0 e le soluzioni x1 e x2 sono, rispettivamente, -1 e 2 quindi:

x² - x - 2 = (x+1)(x-2) con a = 1

Poniamo 2x - 7 A + B .

x² - x - 2 x + 1 x - 2

Con A e B costanti da determinare. Dovremo avere:

2x - 7 Ax - 2° + Bx + B . (A + B )x - 2A + B

(x + 1)(x - 2) (x + 1)(x - 2) (x + 1)(x - 2)

Per il principio di identità poniamo poi:

A + B = 2 A = 3

-2A + B = -7 B = -1

Si avrà infine:

∫ 2x - 7 dx ∫ 3 + -1 dx 3 log | x + 1| - log | x - 2| + C

x² - x - 2 x + 1 x - 2

Secondo caso Δ = 0 :

In questo caso le soluzioni x1 e x2 del polinomio al denominatore della funzione integranda sono coincidenti, cioè:

ax² + bx + c = a ( x - x1) ²

Perciò si lavorerà in modo da ricondurre l'espressione a una qualche integrazione immediata, o semplicemente scomponendola.

Terzo caso Δ < 0 :

In questo caso, infine, non esistono soluzioni reali del polinomio ax² + bx + c ed il polinomio si può esprimere come somma di due quadrati :

ax² + bx + c = a [ (x + k) ² + m ² ]

L'integrale, quindi, si può facilmente ricondurre ad una integrazione immediata.

INTEGRAZIONE PER SOSTITUZIONE-------- ----- ------ -------- ----- ------

Il calcolo di un integrale ∫ f (x) dx può essere più semplice mediante una sostituzione. L'integrale infatti non cambia sostituendo alla variabile d'integrazione x una funzione di un'altra variabile t, purché tale funzione sia derivabile.

Ponendo x = g (t), da cui deriva dx = g' (t) dt si ha che:

∫ f (x) dx = ∫ f [ g (t)] g' (t) dt

Esempio:

1 dx =

x + √x

• Per √x = t x = t²
• Derivando x = t ² avremo : 1 dx = 2 t dt dx = 2 t dt
• A questo punto andiamo a sostituire:

1 2 t dt ∫ 2 t dt ∫ 2 dt 2 log | t + 1 | + C

t² + t t (t + 1) t+1

• E, ritornando alla variabile x :

= 2 log | √x + 1 | + C

INTEGRAZIONE PER PARTI-------- ----- ------ -------- ----- ------ ----- ----- ----

Considerando ora la funzione y formata dal prodotto di due funzioni f (x) e g (x), entrambe derivabili:

y = f (x) g (x)

Derivando il prodotto avremo:

D [f (x) g (x) ] = f ' (x) g (x) + f (x) g' (x)

Integrando ora entrambi i membri otterremo:

∫ [f (x) g (x) ] ' dx = ∫ [f ' (x) g (x) + f (x) g ' (x) ] ' dx

E quindi, semplificando la derivata con l'integrale al primo membro, e componendo il secondo avremo:

f (x) g (x) = ∫ f ' (x) g (x) dx + ∫ f (x) g ' (x) dx

Infine, invertendo semplicemente i membri di questa espressione otterremo la seguente scrittura:

∫ f (x) g ' (x) dx = f (x) g (x) - ∫ f ' (x) g (x) dx

Che rappresenta la regola di integrazione per parti. Chiameremo in questo caso f (x) fattore finito e g ' (x) fattore differenziale.

CAPITOLO 11 TOMO D

INTEGRALI DEFINITI-------- ----- ------ -------- ----- ------ ----- ----- ------------

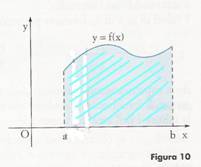
Consideriamo una funzione f (x) continua in un intervallo [a , b] chiuso e limitato.

Vogliamo calcolare la misura dell'area della parte di piano delimitata dall'asse x, dalle rette di equazioni x = a e x = b e dalla curva di equazione y = f (x), grafico della funzione.

Questa parte di piano è anche detta area sottesa dal grafico di f (x) nell'intervallo [a , b] e viene detta trapezoide.

Suddividiamo l'intervallo di ampiezza b - a, in 'n' parti uguali di ampiezza Δx : b - a

n

In ognuno di questi intervalli la funzione è continua perciò ha un valore massimo e un valore minimo che indichiamo rispettivamente con M_k e m_k .

Consideriamo ora le seguenti somme:

_n

s_n = m₁ Δx + m₂ Δx + . + m_n Δx = ∑ m_k Δx

^{k =1}

_n

S_n = M₁ x + M₂ x + . + M_n Δx = ∑ M_k Δx

^{k =1}

Le due somme sono dette rispettivamente somma integrale inferiore e somma integrale superiore della funzione f (x).

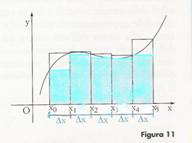
Ciascuno dei rettangoli evidenziati ha base Δx; le misure delle loro altezze sono il valore minimo che la funzione assume in ogni intervallo. Le loro aree perciò misurano m1Δx, m2Δx,... e la somma di queste aree è s_n . Per quanto riguarda invece i rettangoli contornati le loro altezze sono uguali ai valori massimi e le loro aree misurano M1Δx, M2Δx,... la cui somma è S_n.

I valori di s_n e S_n. formano delle successioni che convergono a un unico limite, che rappresenta l'area del trapezoide:

A = I = lim Sn = lim sn

^{n n}

Tale limite si chiama integrale definito della funzione f (x) nell'intervallo [a, b] e si indica con il simbolo:   

_b

∫ f (x) dx

^a

PROPRIETA' INTEGRALI DEFINITI-------- ----- ------ -------- ----- ------ ---

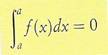Poiché primo e secondo estremo dell'intervallo coincidono, la figura rappresentata dalla seguente scrittura si riduce ad un segmento e quindi la misura della sua area ha valore zero.

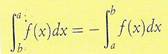Scambiando tra loro gli estremi di integrazione, cambiano segno tutte le somme integrali e quindi cambia segno anche l'integrale.

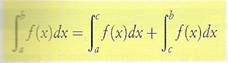Sia f (x) una funzione continua nell'intervallo [a, b] e sia c un punto interno a questo intervallo. L'integrale di f (x) è la somma dei suoi integrali negli intervalli [a, c] e [c, b].

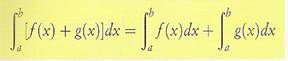L'integrale della somma algebrica (o sottrazione) di due o più funzioni è uguale alla somma ( o sottrazione) degli integrali delle singole funzioni.

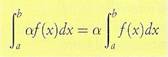Una costante moltiplicativa si può trasportare dentro o fuori del segno di integrale.

CALCOLO INTEGRALE DEFINITO-------- ----- ------ -------- ----- ------ -----

L'integrale definito si calcola secondo la seguente formula:

_{b   b}

∫ f (x) dx = [ F (x) ] = F (b) - F (a)

^{a a}

Ovvero si calcola prima di tutto la primitiva dell'integrale, si sostituisce la variabile x con la variabile a e la variabile b separatamente, e infine si sottraggono le funzioni ottenute.

FUNZIONE INTEGRALE-------- ----- ------ -------- ----- ------ ----- ----- ---------

Sia f (x) una funzione continua nell'intervallo [a, b] e sia x un punto qualsiasi di questo intervallo. Si chiama funzione integrale della funzione in [a, b] la funzione :

_t

F ( x ) = ∫ f (t) dt

^a

la variabile t viene detta variabile di integrazione e può essere sostituita da una qualsiasi altra variabile ( z, c, ecc).

Tale funzione ha le seguenti proprietà:

_{a b}

F ( a) = ∫ f (t) dt = 0 F ( b) = ∫ f (t) dt

^{a a}

TEOREMA DELLA MEDIA-------- ----- ------ -------- ----- ------ ----- ----- ------

Se f (x) è una funzione continua nell'intervallo chiuso e limitato [a, b] , allora esiste almeno un punto c di questo intervallo tale che :

_b

∫ f (x) dx = ( b - a ) f (c)

^a

DIMOSTRAZIONE GRAFICA-------- ----- ------ -------- ----- ------ -------------

Supponendo che f (x) sia positiva nell'intervallo [a, b] e che m e M siano il minimo ed il massimo di tale funzione, l'area sottesa al grafico di f (x) è maggiore dell'area del rettangolo colorato in figura, e minore dell'area del rettangolo contornato.

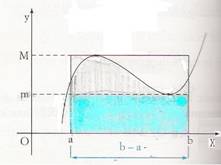m ≤ f (x) ≤ M

Il rettangolo colorato ha la base di misura b - a e altezza m, la sua area perciò è m (b - a)   

_b

ovvero ∫ m dx

^a _b

L'area della funzione f (x), come già detto, misura ∫ f (x) dx ^a

Il secondo rettangolo ha la base di misura b - a e altezza M, la sua area perciò è M (b - a)

_b

ovvero ∫ M dx

^a

^{b b b}

∫ m dx ≤ ∫ f (x) dx ≤ ∫ M dx

^{a a a}

Quindi, come abbiamo appena detto, possiamo scrivere:

_b

m ( b - a ) ≤ ∫ f (x) dx ≤ M ( b - a )

^a

Da cui si ricava la seguente espressione:

_b

m ≤ 1 ∫ f (x) dx ≤ M

b - a ^a

Essendo f (x) una funzione continua, essa assume almeno una volta tutti i valori compresi tra m ed M, perciò esiste almeno un punto c in cui la funzione assume tale valore, cioè:

^b

f (c) = 1 ∫ f (x) dx

b - a ^a

TEOREMA DI TORRICELLI-------- ----- ------ -------- ----- ------ ----- ----- -----

Il legame tra una funzione e la funzione integrata associata ad essa è descritto dal seguente teorema:

se una funzione f (x) è continua nell'intervallo chiuso e limitato [a, b], la corrispondente funzione integrale F (x) è derivabile perciò:

F' (x) = f (x)

DIMOSTRAZIONE-------- ----- ------ -------- ----- ------ ----- ----- --------- ----- ----

Ricordando il concetto di derivata, intesa come limite del rapporto incrementale, possiamo scrivere che la derivata della funzione integrale F (x) è :

F ' (x) = lim F ( x + h ) - F ( x )

h h

Che si può scrivere anche nel seguente modo, dato che F (x + h) e F (x) sono due funzioni integrali:

_{x + h x}

F ' (x) = lim ∫ f ( t ) dt - ∫ f ( t ) dt

^{a a}

h h

Applicando, poi, le proprietà degli stessi integrali, arriviamo alla seguente forma:

_{x + h}  

F ' (x) = lim ∫ f ( t ) dt

^x

h h

Infine, eseguendo il teorema della media con l'estremo b rappresentato da x + h e l'estremo a da x, possiamo affermare che :

F ' (x) = lim h f ( x )

h h

Dove f ( x ) è la funzione f (c) del teorema. A questo punto semplificando la h al numeratore con quella al denominatore ed eseguendo il limite ritorniamo all'uguaglianza enunciata inizialmente, ovvero:

F' (x) = f (x)

CALCOLO DELLE AREE-------- ----- ------ -------- ----- ------ ----- ----- ---------

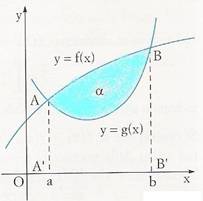Consideriamo ora due funzioni continue f (x) e g (x ) in un intervallo chiuso e limitato [ a, b], i cui grafici si intersecano in due punti A e B.

Supponendo che f (x ) ≥ g (x) , l'area di α ( che chiamiamo S ) è data dalla differenza tra l'area del trapezoide di f (x) e l'area del trapezoide di g (x):

_b

S = ∫ [ f (x) - g (x) dx

^a

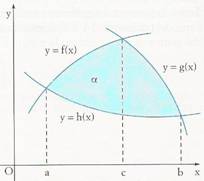
Nel caso in cui dobbiamo determinare l'area ( A )delimitata dal grafico di tre funzioni f (x) , g ( x) e h (x), come in figura, la calcoleremo nel seguente modo:

_{c  b b}

A = ∫ f (x) dx + - ∫ g (x) dx - ∫ h (x) dx

^{a c a}

ESERCIZIO DI ESEMPIO-------- ----- ------ -------- ----- ------ ----- ----- ---------

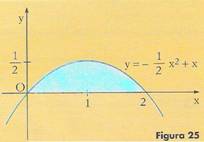
Calcolare l'area della parte di piano delimitata dalla curva di equazione : y = - ½ x ² + x con l'asse x.

Dopo aver disegnato il grafico come in figura, determinando le intersezioni con gli assi, calcoliamo l'area A in questo modo:

_{2 2}

A = ∫ - 1 x ² + x dx = - x³ + x² = - 8 + 4 = 2

⁰ 2 6 2 ⁰ 6 2 3

VOLUME DI UN SOLIDO DI ROTAZIONE-------- ----- ------ ----- ----- --------- ----- -----

Sia y = f (x) una funzione continua nell'intervallo [ a, b]. 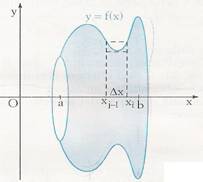consideriamo il trapezoide delimitato dal grafico della funzione e dalle rette x = a e x = b, e facciamo ruotare di un giro completo intorno all'asse x il trapezoide.

Otterremo un solido di rotazione α di cui vogliamo calcolare l'area.

Suddividiamo l'intervallo in 'n' parti uguali di ampiezza Δx = b - a

n

e indichiamo con m_k e M_k i valori minimo e massimo che la funzione assume nell'intervallo.

Avremo, in questo modo, un plurirettangolo inscritto e uno circoscritto al trapezoide, che dopo la rotazione, chiameremo rispettivamente pluricilindro inscritto e pluricilindro circoscritto al solido.

Il pluricilindro inscritto sarà formato dalla somma di 'n' cilindri di altezza Δx e con raggio m_k e il pluricilindro circoscritto sarà formato dalla somma di 'n' cilindri di altezza Δx e con raggio M_k.

Ricordando che il volume di un cilindro di raggio r e altezza h è π r ² h e indicando con v_n e V_n le misure dei volumi dei pluricilindri, avremo:

v_n = m Δx + m Δx + . + m _n Δx

V_n = M Δx + M Δx + . + M _n Δx

I valori di v_n e V_n formano delle successioni che convergono a un unico limite, che rappresenta il volume V del solido di rotazione iniziale :

_b

V = lim Vn = lim vn = ∫ π [ f (x) ] ² dx

^{n n + ∞ a}

CAPITOLO 1 TOMO F

INTEGRALI IMPROPRI DEL PRIMO TIPO-------- ----- ------ ----- ----- --------- ----- ----

Se una funzione f (x) è continua in un intervallo illimitato [ a, + ∞), essa è integrabile in ogni intervallo limitato [ a, t ] con t > a :

_t

∫ f ( x ) dx

^a

dove l'intervallo [ a, t ] è compreso nell'intervallo illimitato.

Diremo quindi che questa funzione f (x) è integrabile in senso improprio se esiste il limite:   

_t

lim ∫ f ( x ) dx

t ^a

Se il limite è finito, l'integrale si dice convergente.

Se invece il limite è infinito, l'integrale si dice divergente.

Se, infine, il limite non esiste, l'integrale si dice indeterminato.

In modo analogo possiamo dire che una funzione f (x) è integrabile in senso improprio nell'intervallo ( - ∞, b ] se esiste il limite:

_b

lim ∫ f ( x ) dx

s ^s

Possiamo infine dire anche che una funzione f (x) è integrabile in senso improprio nell'intervallo ( - ∞, + ∞ ) se esiste il limite:

_t

lim ∫ f ( x ) dx

t ^s

s

Tenendo presente che le variabili t e s devono tendere all'infinito in modo indipendente.

Le definizioni di convergente, divergente e indeterminato valgono per tutti i casi.

ESEMPIO DI INTEGRALE IMPROPRIO DEL PRIMO TIPO-------- ----- ------ ------

_{+ ∞}

∫ 1 dx =

( x + 1 )²

L'Intervallo di tale funzione è [ 2, + ∞ ). Prendiamo quindi la variabile t > 2 e calcoliamo il seguente limite:

_t

lim ∫ 1 dx =

t +∞ ² ( x + 1 )²

_{-1 t}

lim ( x + 1 ) =

t +∞ (- 1) ²

lim - 1 + 1 = 1 .

t +∞ t + 1 3 3

Essendo il limite finito, l'integrale è convergente.

INTEGRALI IMPROPRI DEL SECONDO TIPO-------- ----- ------ ----- ----- -------------

Se una funzione f (x) è continua in un intervallo limitato ma non chiuso, ossia non comprendente almeno uno dei suoi estremi, come [ a, b ) essa è definita per tutti i valori per cui a ≤ x < b ma non è definita in b.

Per questo motivo considereremo l'intervallo [ a, b - ε ] indicando con ε una piccolissima quantità tendente a 0 che chiuderà l'intervallo poco prima del valore b. Avremo quindi il seguente integrale: _{b -}

∫ f ( x ) dx

^a

Diremo quindi che questa funzione f (x) è integrabile in senso improprio nell'intervallo [ a, b ) se esiste il limite:

_{b -}

lim ∫ f ( x ) dx

^a

Se il limite è finito, l'integrale si dice convergente.

Se invece il limite è infinito, l'integrale si dice divergente.

Se, infine, il limite non esiste, l'integrale si dice indeterminato.

In modo analogo possiamo dire che una funzione f (x) è integrabile in senso improprio nell'intervallo ( a, b ] se esiste il limite:

_b

lim ∫ f ( x ) dx

^{a +}

Possiamo infine dire anche che una funzione f (x) è integrabile in senso improprio nell'intervallo ( a, b ) se esiste il limite:

_{b -}

lim ∫ f ( x ) dx

^{a +}

ε2

Tenendo presente che le variabili t e s devono tendere a zero in modo indipendente.

Le definizioni di convergente, divergente e indeterminato valgono per tutti i casi.

ESEMPIO DI INTEGRALE IMPROPRIO DEL SECONDO TIPO-------- ----- ------ -

₄

∫ 1 dx =

¹ x - 1

Inizialmente andiamo ad analizzare il dominio della funzione, che in questo caso è Df : R \ .

Questo significa che la funzione non è definita nel valore 1 e quindi si tratta di un integrale improprio del secondo tipo.

Andiamo a considerare quindi l'Intervallo [ 1 + ε, 4 ] e calcoliamo il seguente limite:

₄

lim ∫ 1 dx =

0 ^{1 +} x - 1

lim log | x - 1 | =

^{1 +}

lim log | 3 | - log | 1 + - 1 | lim log | 3 | . ∞

0 ε 0 log |

Essendo il limite infinito, l'integrale è divergente.

PROPRIETA' DEGLI INTEGRALI IMPROPRI-------- ----- ------ ----- ----- --------------

Sia f (x) una funzione continua nell'intervallo [a, + ∞ ) :

  se f (x) è definitivamente non negativa, ossia f (x) ≥ 0 , il suo integrale può essere convergente o divergente, ma non indeterminato;

  se a < c l'integrale di f (x) nell'intervallo [a,+ ∞) e l'integrale di f (x) nell'intervallo [c, + ∞) hanno lo stesso carattere, cioè sono entrambi convergenti, divergenti o indeterminati e :

_{+∞ c +∞}

∫ f (x) dx ∫ f (x) dx + ∫ f (x) dx

^{a a c}

  se l'integrale di f (x) nell'intervallo [a, + ∞ ) è convergente allora :

_+∞

lim  ∫ f (x) dx = 0

^{t + ∞ t}

  se k è una costante, si ha:

_{+∞ +∞}

∫ k f (x) dx k ∫ f (x) dx

^{a a}

  e, come già detto nelle proprietà degli integrali, abbiamo la seguente uguaglianza:

_{+∞ +∞ +∞}

∫ [ f (x) + g (x) ]dx ∫ f (x) dx + ∫ g (x) dx

^{a a a}

Queste stesse proprietà valgono anche nel caso in cui l'integrale improprio è del secondo tipo!

CRITERI DI CONVERGENZA----- ----- --------------INTEGRALI IMPROPRI 1° TIPO----------

I seguenti criteri ci permettono di stabilire se un integrale improprio converge.

Primo criterio del confronto.

Se per x ≥ b ( con b ≥ a ) le funzioni f (x) e g (x) sono non negative e f (x) ≤ g (x), allora se l'integrale di g (x) nell'intervallo [a, + ∞ ) è convergente, lo è anche l'integrale di f (x) nello stesso intervallo. E se l'integrale di f (x) è divergente, lo è anche l'integrale di g (x).

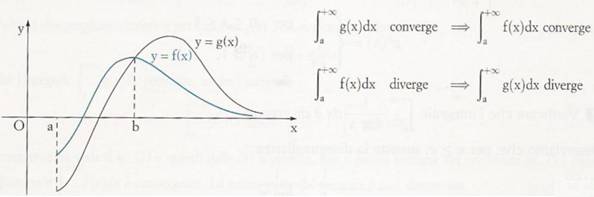
Questo perché la parte di piano sottesa al grafico di y = f (x) nell'intervallo [b, + ∞ ) è contenuta nella parte di piano sottesa al grafico di y = g (x), perciò se questa ultima è finita, anche la prima lo è ( gli integrali convergono ). Viceversa se la prima è infinita, anche la seconda lo è ( divergono ).

Secondo criterio del confronto.

Siano f (x) e g (x) due funzioni non negative per x ≥ b ( con b ≥ a ) e supponendo che per x ≥ b la g (x) non si annulli ed esista il seguente limite:

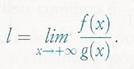
se l'integrale di g (x) nell'intervallo [a, + ∞ ) è convergente e il limite l è finito ( l ≥ 0 ), anche l'integrale di f (x) è convergente.

se l'integrale di g (x) nell'intervallo [a, + ∞ ) è divergente e il limite l è nullo, anche l'integrale di f (x) è divergente.

se il limite l è infinito e l'integrale di g (x) nell'intervallo [a, + ∞ ) è convergente, non si può dire nulla sulla convergenza o meno dell'integrale di f (x).

Criterio di integrabilità.

Per una funzione che conserva o no lo stesso segno nell'intervallo, esiste il seguente criterio:

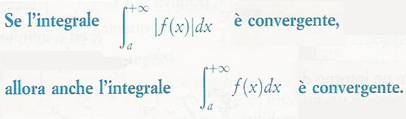
Perché, il fatto che la f (x) del primo integrale è assolutamente convergente, implica la convergenza del secondo.

Questi stessi criteri valgono anche nel caso in cui l'integrale improprio è del secondo tipo!