L'immagine di un generico punto P del piano in una trasformazione T verrà di solito indicata con P', se non vi sono ambiguità. Se per esempio su P agiscono due trasformazioni S e T dovremo indicare le due immagini di P con T(P) ed S(P).

Poiché una trasformazione è una funzione biunivoca, ogni punto del piano ha una ed una sola controimmagine. La funzione che associa ad ogni punto del piano la sua controimmagine è la funzione inversa della funzione assegnata e sarà a sua volta una trasformazione. Perciò:

Data una trasformazione T del piano in sé, si dice trasformazione inversa di T e si indica con T^-1 la trasformazione che associa ad ogni punto la sua controimmagine mediante T.

Tra le trasformazioni del piano noi considereremo solo quelle che hanno la notevole proprietà di trasformare rette in rette.

Definizione Si dice affinità una trasformazione del piano che trasforma rette in rette

Teorema Una affinità trasforma punti allineati in punti allineati.

Dimostrazione. Supponiamo che i punti P, Q ed R siano allineati e che sia un'affinità. Se per assurdo R' non appartenesse alla retta P'Q' allora l'immagine della retta PQ dovrebbe contenere tre punti non allineati e quindi non potrebbe essere una retta, contro l'ipotesi che sia un'affinità.

Teorema Un'affinità trasforma rette parallele in rette parallele e rette incidenti in rette incidenti.

Dimostrazione. Per ipotesi supponiamo che le rette r ed s siano parallele e che r' ed s' siano le loro rispettive immagini. Per assurdo supponiamo che r' ed s' siano incidenti, cioè che esista un punto P' nella loro intersezione (in simboli: = r' ∩ s'). P' ha una sola controimmagine P perché l'affinità è una corrispondenza biunivoca. Questa controimmagine P deve appartenere sia ad r che ad s e ciò significa che r ed s dovrebbero essere incidenti, contro l'ipotesi. c.v.d.

Corollario Ogni parallelogramma viene trasformato in un altro parallelogramma da un'affinità

Teorema Il punto medio di un segmento viene trasformato nel punto medio del segmento trasformato.OPPURE:Le affinità conservano i punti medi dei segmenti.

Traccia per la dimostrazione: il punto medio di un segmento può sempre essere visto come il centro di un parallelogramma che ha tale segmento per diagonale. Il parallelogramma si trasformerà in un altro parallelogramma che ha per centro il trasformato del centro del primo (perché?)

Teorema Ogni affinità conserva la natura delle coniche.

In altri termini ellissi vengono trasformate in ellissi, parabole in parabole ed iperboli in iperboli.

La circonferenza viene trasformata, in generale, in un'ellisse ed il suo centro nel centro dell'ellisse.

Teorema Le affinità conservano i rapporti tra le aree

Cioè se due figure F e G stanno in rapporto k tra loro, anche le due figure trasformate F' e G' stanno nello stesso rapporto k. Questo significa che se il rapporto tra F' ed F è r, allora anche il rapporto tra G' e G è r; in altre parole un'affinità moltiplica l'area di ogni figura per uno stesso fattore r che viene chiamato rapporto di affinità.

Fissiamo ora nel piano un sistema di riferimento cartesiano. Posto di indicare con x ed y le coordinate di un generico punto P e con x' ed y' le coordinate del suo trasformato, si dimostra il seguente:

Teorema In ogni affinità i legami tra x;y e x';y' sono i seguenti: con la condizione che

Le due equazioni precedenti si chiameranno equazioni dell'affinità. Si dirà invece matrice dell'affinità la matrice che dovrà avere necessariamente determinante non nullo.

Osserviamo subito che i parametri che compaiono nelle equazioni sono sei, per cui occorrono sei condizioni per calcolarne il valore. Per esempio si può dimostrare che se conosco le coordinate dei vertici di un triangolo non degenere e le coordinate dei trasformati, allora riesco ad individuare le equazioni dell'affinità. Infatti sostituendo nelle equazioni dell'affinità generica le coordinate note ottengo esattamente sei condizioni sui parametri.

Osserviamo infine che le equazioni delle affinità possono essere scritte in forma matriciale:

dove:

Teorema Data un'affinità con matrice A, il suo rapporto di affinità è uguale al modulo del determinante di A.

Definizione Una trasformazione si dice diretta se conserva l'orientamento degli angoli, altrimenti si dice indiretta[1] (o contraria).

In altre parole, detti A, B e C i vertici di un triangolo e A', B' e C' i loro corrispondenti in una trasformazione T, supponiamo di percorrere il bordo del triangolo ABC in senso orario. Se i vertici di A'B'C' sono disposti in modo tale che il percorso A'B'C' sia orario, allora l'orientamento è conservato, altrimenti l'orientamento non è conservato.

Teorema Un'affinità è diretta o contraria a seconda che il determinante della sua matrice sia rispettivamente positivo o negativo.

Definizione Si chiama punto unito (o invariante, o fisso) di una trasformazione T un punto P che sia immagine di se stesso, ovvero tale che P= P'.

Per calcolare le coordinate dei punti uniti di un'affinità, si deve porre, nelle equazioni dell'affinità, x' =x ed y' = y perché un punto è unito quando l'immagine P'(x',y') coincide con il punto di partenza P(x,y). Ne deriva un sistema lineare.

Se quest'ultimo sistema è determinato, si ha un solo punto unito.

Se è indeterminato, si ha una retta di punti uniti, a meno che tutto il piano sia unito, nel qual caso la trasformazione studiata è l'identità.

Se il sistema è impossibile non si hanno punti uniti.

Si deduce, come conseguenza, che, se una trasformazione ha due punti uniti, allora tutta la retta che passa per essi è luogo di punti uniti, se invece ha tre punti uniti non allineati, allora è l'identità.

Si chiama retta unita (o invariante, o fissa) per una trasformazione T una retta r che sia immagine di se stessa, ovvero tale che r = T(r).

In particolare: se ogni punto di r è unito, la retta si dice puntualmente unita; in caso contrario, si dice globalmente unita.

Affinità inversa

Date le equazioni di un'affinità, per ottenere le equazioni dell'affinità inversa, si può procedere in due modi:

si esplicitano x ed y in funzione di x' ed y'

si moltiplicano entrambi i membri della (1) per la matrice inversa di A

Per verificare quest'ultimo punto usiamo la scrittura matriciale e ricaviamo X in funzione di X' : da si ha ed infine, moltiplicando per a sinistra, (2) . E' solo il caso di osservare che la matrice A è senz'altro invertibile per la condizione che il suo determinante è diverso da zero. Dall'ultima relazione si trova che il determinante dell'affinità inversa è il reciproco del determinante dell'affinità di partenza (basta utilizzare una proprietà dei determinanti) e quindi la stessa relazione vale per il rapporto di affinità. Inoltre si vede che l'inversa di un'affinità diretta è ancora diretta e l'inversa di una contraria è contraria.

Osservazioni

Per trovare le coordinate dei punti trasformati, si usano le equazioni dirette (1), mentre, per scrivere le equazioni delle curve trasformate, si utilizzano le equazioni inverse (2), poiché vanno inseriti x ed y in funzione di x' e di y'.

Prodotto di due affinità.

L'insieme delle affinità di un piano in sé può essere strutturato con un'operazione detta prodotto di affinità, che coincide con la composizione di due funzioni:

Definizione Date due affinità U e V, si chiama prodotto (o trasformazione composta) delle due affinità, la corrispondenza T tra i punti del piano che si ottiene eseguendo prima l'affinità U e poi l'affinità V e si scrive: T = VU (attenzione all'ordine!!). In altre parole, dato il punto P, ad esso si applica per prima la trasformazione U ed al punto trasformato P' si applica la trasformazione V. Si ottiene un punto P'' e si considera la trasformazione che associa a P il punto P''. Se U e V sono affinità, si vede dalla definizione che anche T lo deve essere.

Teorema Se l'affinità U ha matrice A e l'affinità V ha matrice B allora l'affinità VU ha matrice BA ed il rapporto di affinità della matrice prodotto è il prodotto dei rapporti di affinità di U e V.

Dimostrazione. Usiamo la forma matriciale per scrivere le equazioni delle affinità. Se il punto P ha coordinate X allora P' avrà coordinate ed il punto P'' avrà coordinate . Sostituendo in quest'ultima le coordinate di P' si ha: cioè: con cui si ottiene la prima parte della tesi. Per quanto riguarda il resto basta osservare che il rapporto di affinità del prodotto è dato da , dove abbiamo usato il teorema di Binet ed una notevole proprietà del valore assoluto. c.v.d.

Come conseguenza del teorema si verifica in particolare che: il prodotto di due equivalenze è un'equivalenza; il prodotto di due affinità dirette o di due contrarie è un'affinità diretta, mentre il prodotto tra un'affinità diretta ed una contraria dà un'affinità contraria.

Poichè:

Il prodotto di due affinità è ancora un'affinità

Il prodotto di due affinità gode della proprietà associativa

Nell'insieme delle affinità esiste l'elemento neutro, che è l'identità

Ogni affinità ammette l'elemento inverso rispetto al prodotto

possiamo concludere che l'insieme delle affinità, strutturato con il prodotto, è un gruppo (non abeliano).

Inseriamo qui l'importante

Definizione Una trasformazione T si dice involutiva se TT = I, cioè se applicata due volte dà l'identità.

Si dimostra subito, (è lasciato per esercizio) utilizzando per esempio la scrittura matriciale, che un'affinità involutiva coincide con la sua inversa e che è in ogni caso un'equivalenza.

Similitudini

Definizione Si dice similitudine un'affinità che moltiplica le distanze per un numero positivo k che viene detto rapporto di similitudine. In simboli, un'affinità è una similitudine se, dati due punti P e Q nel piano, si ha: .

Raccogliamo in un teorema le principali proprietà invarianti di una similitudine:

Teorema Una similitudine:

conserva la misura degli angoli, cioè angoli corrispondenti sono isometrici.

conserva la relazione di perpendicolarità tra rette.

trasforma cerchi in cerchi.

trasforma poligoni regolari in poligoni regolari con lo stesso numero di lati.

Per quanto riguarda le equazioni di una similitudine si dimostra (esercizio) che:

Teorema La matrice di una similitudine può essere unicamente della forma (similitudine diretta) oppure della forma (similitudine contraria). Viceversa ogni affinità che ha matrice di una delle forme descritte è una similitudine.

Osserviamo che il rapporto di affinità per ciascuna delle matrici date è uguale a , quindi si trova subito che il rapporto di similitudine vale (dimostralo osservando come si trasforma il quadrato che ha lato generico PQ).

E' anche facile convincersi che:

Teorema Il prodotto di due similitudini è una similitudine che ha per rapporto di similitudine il prodotto dei rapporti di similitudine dei fattori. Inoltre l'insieme delle similitudini del piano costituisce un gruppo (non abeliano) rispetto al prodotto di trasformazioni. L'inversa di una similitudine quindi è ancora una similitudine con rapporto uguale al reciproco del rapporto della similitudine di partenza.

Omotetie

Definizione Si dice omotetia di centro C e rapporto h (con h reale e diverso da zero) la trasformazone che associa al punto P del piano l'unico punto P' tale che .

Le omotetie corrispondono in sostanza agli "zoom" centrati in C; in particolare lo "zoom" è un ingrandimento se ed è una riduzione se . Per si ha l'identità, mentre per si ha la simmetria centrale di centro C. Si intuisce quindi che deve valere il seguente:

Teorema Ogni omotetia di centro C e rapporto h è una similitudine di rapporto uguale al modulo di h. Inoltre le omotetie conservano le direzioni, cioè trasformano rette in rette ad esse parallele.

Dimostrazione Considero i punti P e Q del piano ed i loro trasformati secondo l'omotetia di rapporto h. Supponiamo per fissare le idee che h sia positivo. Allora si dimostra subito che i triangoli PQC e P'Q'C sono simili per il primo criterio di similitudine avendo un angolo in comune ed i lati adiacenti in proporzione. Quindi i segmenti PQ e P'Q' sono paralleli tra loro e stanno in rapporto h. Alla tesi si arriva osservando che i punti P e Q sono stati presi ad arbitrio e quindi la conclusione vale in ogni caso. Allo stesso risultato, ma con considerazioni diverse, si arriva scegliendo h negativo. c.v.d.

Si può anche facilmente dimostrare che ogni omotetia ha le seguenti equazioni: in cui h rappresenta proprio il rapporto di omotetia. Dalle equazioni di un'omotetia si ricavano facilmente anche le coordinate del suo centro osservando che esso è il suo unico punto unito.

Viceversa, se conosciamo le coordinate del centro C dell'omotetia di rapporto h, le sue equazioni saranno: .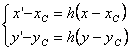

Osserviamo che ogni omotetia è un'affinità diretta ed il suo rapporto di affinità è uguale a .

Anche l'insieme delle omotetie del piano con lo stesso centro C costituisce un gruppo rispetto al prodotto di trasformazioni. Il rapporto di omotetia del prodotto di due omotetie di rapporti h e k è il prodotto hk dei rapporti. In generale invece il prodotto di due omotetie con centri diversi è ancora un'omotetia, con un centro distinto dai primi due, ma è una traslazione se le due omotetie hanno rapporti reciproci tra loro.

E' facile dimostrare che ogni retta passante per il centro di omotetia è globalmente unita e non ve ne sono altre, a meno che .

Isometrie

Definizione Si chiama isometria piana ogni affinità che conserva le distanze, cioè che trasforma segmenti in segmenti ad essi congruenti. In altri termini un'isometria è una similitudine di rapporto uguale ad uno, o, se si preferisce, una similitudine che è anche un'equivalenza.

Dalla definizione si ricava subito il seguente

Teorema Il prodotto di due isometrie è un'isometria. Inoltre l'insieme delle isometrie del piano costituisce un gruppo (non abeliano) rispetto al prodotto di trasformazioni. L'inversa di un'isometria è un'isometria.

Tutte le isometrie si classificano facilmente in quattro gruppi secondo il seguente schema, che sarà molto utile quando si tratterà di riconoscere un'isometria dalla sua equazione:

Traslazioni

Definizione Si dice traslazione di vettore la trasformazione dei punti del piano che associa al punto P l'unico punto P' tale che il vettore sia equivalente a .

Dimostra per esercizio che una traslazione è un'isometria.

L'insieme delle traslazioni del piano costituisce un gruppo abeliano rispetto alla composizione di trasformazioni. Questo risultato discende immediatamente dall'osservazione che il prodotto di due traslazioni di vettori ed coincide con la traslazione di vettore . Si dice, in termini tecnici, che il gruppo delle traslazioni è isomorfo al gruppo dei vettori del piano dotato dell'operazione di somma. Osserviamo anche che l'inversa della traslazione di vettore coincide con la traslazione di vettore e l'identità può anche essere pensata come la traslazione di vettore nullo.

Le equazioni della traslazione di vettore sono: .

Una traslazione non ha punti uniti (a meno che.), mentre sono unite tutte le rette parallele a .

Rotazioni

Definizione Si dice rotazione di centro C ed angolo orientato la trasformazione che associa ad un punto P del piano l'unico punto P' tale che e che l'angolo misuri .

Dimostra per esercizio che una rotazione è un'isometria.

L'insieme delle rotazioni del piano con lo stesso centro costituisce un gruppo abeliano rispetto alla composizione di trasformazioni. Questo risultato discende immediatamente dall'osservazione che il prodotto di due rotazioni con lo stesso centro C e di angoli e coincide con la rotazione di centro C ed angolo . Si dice, in termini tecnici, che il gruppo delle rotazioni con lo stesso centro è isomorfo al gruppo additivo dei numeri reali. Osserviamo anche che l'inversa della rotazione di angolo coincide con la rotazione di angolo e l'identità può anche essere pensata come la rotazione di angolo nullo.

Le equazioni della rotazione di centro ed angolo sono: .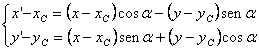

Una rotazione ha un solo punto unito, il suo centro (a meno che.), mentre in generale non ha rette unite. Fanno eccezione: l'identità ed il caso notevole della rotazione di 180° che coincide con la simmetria centrale di centro C e che ha quindi infinite rette unite.

Si dimostra che componendo due rotazioni di angoli e con centri diversi si ottiene ancora una rotazione di angolo oppure una traslazione se .

Infine osserviamo che componendo una rotazione di centro C ed angolo con una traslazione si ottiene una rotazione di angolo e centro C'. Quindi l'insieme delle rotazioni e delle traslazioni del piano costituisce un gruppo (non abeliano) che coincide con il gruppo dei movimenti rigidi del piano.

Notiamo infine che le equazioni della simmetria centrale di centro si possono ottenere dalla definizione e sono: .

Simmetrie assiali

Definizione Si dice simmetria assiale di asse r la trasformazione del piano che associa al punto P l'unico punto P' tale che r sia l'asse del segmento PP'.

Dimostra per esercizio che una simmetria assiale è un'isometria.

La simmetria assiale è una trasformazione involutiva. L'identità non è una simmetria assiale, perciò l'insieme delle simmetrie assiali non è un gruppo.

Non scriviamo qui l'equazione generale della simmetria assiale, ma scriviamo le equazioni di simmetrie rispetto a rette notevoli:

; ; ;

La simmetria assiale ha infiniti punti uniti: tutti i punti dell'asse. Le rette unite sono, oltre all'asse, tutte le rette ad esso perpendicolari. La direzione dell'asse e quella ad esso perpendicolare sono unite.

Componendo tra loro due simmetrie assiali si deve ottenere un'isometria diretta. In particolare si avrà:

una rotazione se i due assi sono incidenti; in tal caso la rotazione avrà per centro il punto di intersezione degli assi ed angolo pari al doppio dell'angolo da essi formato

una traslazione se i due assi sono paralleli

Glissosimmetrie

Definizione Una glissosimmetria di asse r e vettore ( deve essere non nullo e parallelo ad r) è il prodotto di una traslazione di vettore con una simmetria di asse r.

E' ovvio che una glissosimmetria è un'isometria, essendo il prodotto di due isometrie. L'insieme delle glissosimmetrie non è un gruppo.

Una glissosimmetria non ha punti uniti, mentre l'unica retta unita è il suo asse r. La direzione di r è unita.

Quando si sia riconosciuto che le equazioni di un'isometria sono quelle di una glissosimmetria, il suo asse si determina trovando la retta unita, mentre il suo vettore si trova scegliendo ad arbitrio un punto P sull'asse e trovando le coordinate del suo trasformato P'. Il vettore cercato è il vettore .

---