|
|
| |
Matematica - Preparazione al compito per l'orale:
1 - Funzioni esponenziale e logaritmica con relativi grafici e proprietà
2 - Funzioni in R
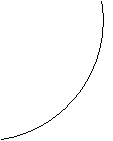
1.1) 626c28g 626c28g Funzione esponenziale
![]()
![]()
![]() BASE MAGGIORE DI 1 BASE
COMPRESA FRA 0 E 1
BASE MAGGIORE DI 1 BASE
COMPRESA FRA 0 E 1
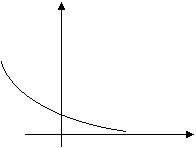
CARATTERISTICHE.
· 626c28g Assume solo valori positivi
· 626c28g Passa per P(0,1)
· 626c28g Ha come asintoto l'asse delle x
· 626c28g a>1 è crescente
· 626c28g 0<a<1 è decrescente
· 626c28g Dominio: R
· 626c28g Codominio: R+
Quando una funzione è espressa mediante un numero elevato all'esponente la funzione è detta funzione esponenziale , ha come base un numero e come esponente la variabile indipendente espressa da un numero reale (R).
La funzione esponenziale è sempre positiva e viene definita solo se la base è ≠0 o >0
Se la base è >1:
1. 626c28g la funzione è crescente all'aumentare delle x aumentano le y;
2. 626c28g D: ]-∞;+∞[
3. 626c28g la funzione passa per il punto 0;1
4. 626c28g quando la x tende ad assumere valori verso +∞ anche la y tende ad assumere valori verso +∞
Se la base è compresa tra 0;1
1. 626c28g la funzione è decrescente,
2. 626c28g D: ]-∞;+∞[ ,
3. 626c28g quando la x tende ad assumere valori verso +∞, la y assume valori che i avvicinano allo 0 senza mai raggiungerlo
4. 626c28g quando la x tende ad assumere valori verso -∞, la y assume valori verso +∞
Quando abbiamo una funzione esponenziale che ha l'esponente con una funzione algebrica, per ottenere il dominio D si applica alla funzione algebrica le regole delle funzioni razionali o irrazionali, intere o fratte.
La funzione esponenziale con 0<a<1 e quella con a>1 sono simmetriche rispetto all'asse y. È monotona, biiettiva e invertibile in R (la sua inversa è proprio la funzione logaritmica).
1.2) Funzione logaritmica
![]() BASE MAGGIORE DI 1 BASE
COMPRESA FRA 0 E 1
BASE MAGGIORE DI 1 BASE
COMPRESA FRA 0 E 1
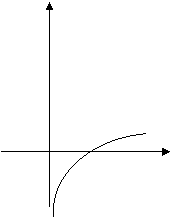
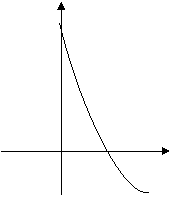
CARATTERISTICHE
· 626c28g Passa per P(1,0)
· 626c28g Ha come asintoto l'asse y
· 626c28g È decrescente
· 626c28g Dominio: R+
· 626c28g Codominio: R
Dati due numeri positivi a e b con a≠1, si chiama logaritmo in base a del numero b l'esponente da dare ad a per ottenere b.
PROPRIETA' DEI LOGARITMI
1. 626c28g Log a b * c = Log a b + Log a c
Il logaritmo di un prodotto è = alla somma dei logaritmi dei singoli fattori
Log a b/c = Log a b - Log a c
Il logaritmo di un quoziente è uguale alla differenza del logaritmo del numeratore e del logaritmo del denominatore
Log a bc = c * Log a b
Log a ⁿ √ b m = m/n * Log a b
Il logaritmo di un elevamento a potenza (o radice) è uguale all'esponente moltiplicato per il logaritmo
Log a b = Log 10 b / Log 10 a
Proprietà del cambiamento di base
La funzione logaritmica con 0<a<1 e quella con a>1 sono simmetriche rispetto alla bisettrice del primo e terzo quadrante.
2.1) Gli intervalli limitati
Definizione
Dati due numeri reali a e b, con a<b, si dice:
- Intervallo aperto: l'insieme di tutti i numeri reali tali che a<x<b e si indica con (a,b) o ]a,b[.
- Intervallo chiuso: l'insieme di tutti i numeri reali tali che a≤x≤b e si indica con [a,b].
- Intervallo aperto a destra: l'insieme di tutti i numeri reali tali che a<x ≤ b e si indica con [a,b).
- Intervallo aperto a sinistra l'insieme di tutti i numeri reali tali che a ≤ x < b e si indica con (a,b].
2.2) Gli intervalli illimitati
Definizione
- Un intervallo si dice illimitato superiormente quando e si indica con (a,+∞) o [a, +∞)
- Un intervallo si dice illimitato inferiormente quando e si indica con (a,-∞) o (a, -∞]
2.3) Gli intorni
Definizione
- Intorno completo: un qualsiasi intervallo aperto che contenga il numero c.
- Intorno destro: un qualsiasi intervallo aperto a destra che abbia come estremo sinistro il numero c.
- Intorno sinistro: un qualsiasi intervallo aperto a sinistra che abbia come estremo destro il numero c.
Proprietà
- L'intersezione di due o più intorni di c è ancora un intorno.
- Per ogni coppia di punti distinti a e b ![]() R esistono un intorno
di a e uno di b disgiunti.
R esistono un intorno
di a e uno di b disgiunti.
- Un insieme E è limitato superiormente quando esiste un numero reale b che risulta ≥ ad ogni numero di E
- Un insieme E è limitato inferiormente quando esiste un numero reale a che risulta ≤ ad ogni numero di E.
2.4) Relazione fra punto e insieme
Definizione
Un punto si dice:
- Interno all'insieme E: se esiste un intorno di c interamente costituito da punti che appartengono ad E.
- Esterno all'insieme E: se esiste un intorno di c che non contenga alcun punto di E, cioè sia costituito solo da punti appartenenti al complementare di E.
- Di frontiera per E: se non è né interno né esterno ad E, ovvero se in un qualsiasi intorno di c cadono almeno un punto di E, e almeno un punto del complementare di E.
- Di accumulazione per E: se in ogni intorno di c cadono infiniti punti di E;
- Isolato per E: se esiste un intorno di c nel quale l'unico punto di E è c.
2.5) Estremi
Definizione
Un numero s si dice estremo superiore di un insieme non vuoto E se:
- Ogni numero di E non supera s;
- Comunque si fissi ε>0, esiste in E almeno un numero maggiore di s - ε.
Un numero i si dice estremo superiore di un insieme non vuoto E se:
- Ogni numero di E è ≥ i;
- Comunque si fissi ε>0, esiste in E almeno un numero maggiore di i + ε.
2.6) Funzioni
Definizione
Dati due insiemi non vuoti A e B si chiama funzione di A in B una qualsiasi legge che associa ad ogni elemento di A uno ed un solo elemento di B.
Proprietà
- Una funzione si dice costante se l'insieme A contiene un solo numero
- Una funzione si dice identità quando associa ad ogni elemento di A l'elemento stesso.
- Due funzioni sono uguali se hanno dominio, codominio e legge uguali.
- Una funzione si dice suriettiva quando ogni elemento di B è immagine di almeno un elemento di A.
- Una funzione si dice iniettiva quando fa corrispondere ad elementi distinti di A elementi distinti di B.
- Una funzione si dice biiettiva o corrispondenza biunivoca quando esiste una legge che associa ad ogni elemento di A uno ed un solo elemento di B e viceversa.
2.7) Grafici delle funzioni
Definizione
Si chiama grafico di una funzione f di A in B l'insieme G di tutte le coppie ordinate (x,y) che si ottengono prendendo un valore di per in A e trovando il corrispondente y = f(x) in B.
2.8) Tipi di funzione
Definizione
Una funzione f: A→R si dice:
- Pari se risulta f (-x) =f (x)
- Dispari se risulta f (-x) = - f(x)
Monotona:
Definizione:
Sia f(x) una funzione reale della variabile reale x, definita nell'insieme A, e A contenga almeno due punti. Quando per ogni coppia di punti x1 e x2 di A risulta:
- x1 < x2![]() f(x1)<f(x2) la funzione si dice crescente in A
f(x1)<f(x2) la funzione si dice crescente in A
- x1 < x2![]() f(x1)>f(x2) la
funzione si dice decrescente in A
f(x1)>f(x2) la
funzione si dice decrescente in A
- x1 < x2![]() f(x1)≤ f(x2) la funzione si dice non decrescente in A
(crescente e costante)
f(x1)≤ f(x2) la funzione si dice non decrescente in A
(crescente e costante)
- x1 < x2![]() f(x1)≥ f(x2) la funzione si dice non crescente in A
(decrescente e costante)
f(x1)≥ f(x2) la funzione si dice non crescente in A
(decrescente e costante)
Periodica:
Definizione
Una funzione si dice periodica di periodo T≠0 se
![]() x
x![]() A, x
A, x![]() A
A ![]() (x+T)
(x+T) ![]() A e f(x+T) =f(x)
A e f(x+T) =f(x)
Composta:
Definizione
Date le funzioni g: A→B ed f: C→D con z =
g(x), y = f(x) e g(A)![]() C, si chiama funzione composta di g ed f (nell'ordine) la
funzione h: A→C tale che h(x) = f (x)
C, si chiama funzione composta di g ed f (nell'ordine) la
funzione h: A→C tale che h(x) = f (x)![]() g(x)
g(x) ![]() A.
A.
Proprietà
- La funzione composta non gode della proprietà commutativa.
- Occorre saper individuare le componenti di una funzione composta.
2.9) Determinazione del dominio di una funzione: tipologie
1. 626c28g Le operazioni di somma, differenza e prodotto sono sempre possibili e quindi hanno dominio R.
2. 626c28g La divisione è sempre possibile, purché il denominatore sia ≠ 0.
3. 626c28g L'estrazione di radice è possibile quando:
- Con indice pari, il radicando è ≥ 0
- Con indice dispari è possibile per ogni x escluse quelle che annullerebbero un eventuale denominatore
4. 626c28g Le funzioni goniometriche seno e coseno
esistono ![]() R; la funzione tangente esiste
R; la funzione tangente esiste ![]() x≠ (π/2)+k π; la funzione cotangente esiste
x≠ (π/2)+k π; la funzione cotangente esiste ![]() x≠ k π
x≠ k π
5. 626c28g Il logaritmo di un numero, di qualsiasi base positiva e diversa da 1, esiste soltanto quando l'argomento è positivo.
2.10) Funzioni inverse
Definizione
Data una funzione biiettiva f di A su B, si chiama
inversa della f la funzione biiettiva f -1 di B su A, tale che
f -1![]() f =i A e f
f =i A e f ![]() f -1 =i B
f -1 =i B
Una funzione è invertibile se e solo se è biiettiva.
Se una funzione è crescente (o decrescente) allora ammette la funzione inversa, che è anch'essa crescente (o decrescente)
Arcoseno
Funzione: y = sen x Dominio:[-π/2,π/2] Codominio:[-1,1]
Inversa: y = arcsen x Dominio:[-1,1] Codominio:[-π/2,π/2]
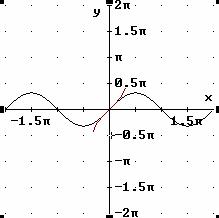
Arcocoseno
Funzione: y = cos x Dominio:[0,π] Codominio:[-1,1]
Inversa: y = arccos x Dominio:[-1,1] Codominio:[0,π]
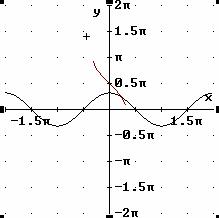
Tangente
Funzione: y = tg x Dominio:[-π/2,π/2] Codominio:[-∞, ∞]
Inversa: y = arctg x Dominio:[ -∞, ∞] Codominio:[-π/2,π/2]
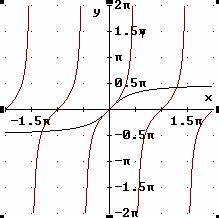
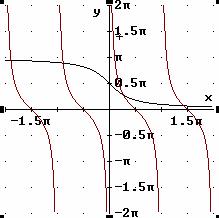
Cotangente
Funzione: y = ctg x Dominio:[ 0,π] Codominio:[-∞, ∞]
Inversa: y = arcctg x Dominio:[ -∞, ∞] Codominio:[ 0,π]
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025