LA VARIABILITÀ

E(p) è massimo quando p_i = 1/k per ogni i

E(p) è minimo quando (k - 1) p_i = 0 e una sola p_i = 1;

E(p) diminuisce o al più resta costante se, data la disuguaglianza 0 < p_r < p_s e la quantità δ > 0,

p_r e p_s risultano rispettivamente diminuita ed aumentata della stessa quantità δ;

se E(p) ..

L'indice di eterogeneità del Gini e

che assume come valore minimo E₁=0 e come valore massimo E₁=(k - 1)/k.

La normalizzazione dell'indice, cioè la possibilità di variare tra 0 e 1 si ottiene dividendo E₁ per il suo massimo valore

2 La variabilità dei fenomeni quantitativi: gli indici di dispersione

Indicato con α=α(x₁, .., x_n) un generico indice di posizione calcolato sulla v.s. X=(x₁, .., x_n), si chiama indice di dispersione intorno ad α la media delle distanze |x_i - α| (per i che va da 1 a n).

L'indice di dispersione è espresso nella stessa unità di misura della variabile X; per questo motivo è anche una misura della dispersione della variabile.

Si ha un indice di dispersione intorno ad α, indicato con D(X)=D(x₁, .., x_n), se vengono soddisfatte le seguenti proprietà:

D(X)≥0

D(X)=0 se la distribuzione della v.s. è degenere (si dice degenere un fenomeno che assume sulle n unità osservate la stessa modalità);

- D(X + c)=D(X) se ogni x_i viene sostituito da x_i + c (l'indice è invariante per traslazione);

D(X)≥D(Y) se date due variabili statistiche X=(x₁, .., x_n) e Y=(y₁, .., y_n) si ha |x_i - α| ≥ |y_i - α| (per i che va da 1 a n) con disuguaglianza stretta per qualche i.

La più comune specificazione di un indice di dispersione discende dalla media potenziata degli scarti assoluti |x_i - α|, vale a dire 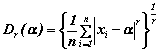(2 a)

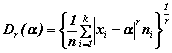
    con n_i = frequenze assolute (2 b)

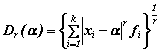
    con f_i = frequenze relative (n_i/n) (2 c)

2.1 Lo scarto assoluto medio e lo scarto quadratico medio dalla mediana

Per a=M_e ed r=1 le formule (2 a), (2 b) e (2 c) forniscono lo scarto assoluto medio dalla mediana, semplice

e ponderato con n_i = frequenze assolute

con f_i = frequenze relative (n_i/n)

che gode della nota proprietà di minimo della mediana.

Per a = M_e ed r = 2 le formule (4.2 a), (42 b) e (4.2 c) forniscono lo scarto quadratico medio dalla mediana semplice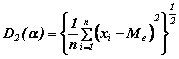

e ponderato 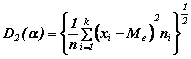con n_i = frequenze assolute

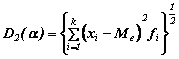con f_i = frequenze relative (n_i/n)

2.2 Lo scarto assoluto medio e lo scarto quadratico medio dalla media aritmetica

Per a= ed r=1 le formule (2 a), (2 b) e (2 c) forniscono lo scarto assoluto medio dalla media aritmetica semplice

e ponderato con n_i = frequenze assolute

con f_i = frequenze relative (n_i/n)

Per a ed r=2 le formule (2 a), (2 b) e (2 c) forniscono lo scarto quadratico medio semplice

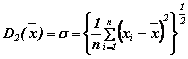
e ponderato 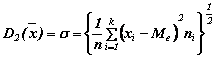con n_i = frequenze assolute

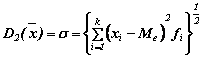con f_i=frequenze relative (n_i/n)

2.3 La varianza = s

Si dice varianza la media dei quadrati degli scarti dalla media aritmetica. La varianza è il quadrato dello scarto quadratico medio

con n_i = frequenze assolute

con f_i = frequenze relative (n_i/n)

- Calcolo abbreviato della varianza

Dalla formula si ottiene la relazione che

nel caso di indice semplice assume la forma  

nel caso di indice ponderato assume la forma con n_i = frequenze assolute

con f_i = freq. relative (n_i/n)

- Proprietà della varianza

* la varianza è invariante per traslazione Var(X)=Var(X + a)

* Var(a + bX) = b²Var(X)

- Teoremi della varianza

* La varianza di un miscuglio di k gruppi

dove è la media ponderata delle varianze dei singoli gruppi

e è la varianza ponderata delle medie dei singoli gruppi

* Varianza della somma di due variabili statistiche Z = X + Y

Var(X + Y)=Var(X) + Var (Y)+2Cov((X, Y)

* Varianza della differenza di due variabili statistiche Z = X - Y

Var(X - Y)=Var (X)+Var(Y)-2Cov (X, Y)

La varianza della somma o della differenza di due variabili statistiche tra loro indipendenti (cioè con covarianza nulla) è in ogni caso pari alla somma o alla differenza delle varianze delle due variabili.

2.4 La covarianza

La covarianza di due variabili X e Y è definita come la media dei prodotti degli scarti di X e Y dalle rispettive medie   

Una formula utile per il calcolo esprime la covarianza come la media del prodotto dei valori di X e Y meno il prodotto delle medie delle due variabili statistiche

3 La variabilità dei fenomeni quantitativi: gli indici di forma

Gli indici di forma misurano l'asimmetria (o curtosi) della curva di distribuzione di una variabile statistica.

Nelle distribuzioni unimodali simmetriche (v. la gaussiana) Moda, Mediana e Media aritmetica coincidono.

Nelle distribuzioni unimodali asimmetriche si possono presentare due casi:

- asimmetria positiva (ramo ascendente della curva più ripido di quello discendente) Mo < Me <

- asimmetria negativa (ramo discendente della curva più ripido di quello ascendente) < Me < Mo

Un indice che misura l'asimmetria di una curva di distribuzione è l'indice relativo di asimmetria del Fisher

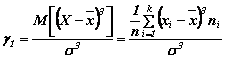
L'indice è nullo quando è nullo il numeratore e la distribuzione è simmetrica, assume valori positivi se gli scarti positivi al cubo prevalgono complessivamente su quelli negativi al cubo, assume valori negativi quando si invertono le predette prevalenze, denotando conseguentemente una asimmetria negativa.

Essendo il denominatore sempre positivo, il segno dell'indice è dato dal segno del numeratore.