|
|
| |
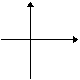
Y=mx retta passante per l'origine del piano cartesiano
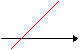
Y=mx+q retta in posizione generica ( cioè interseca l'ordinata,l'asse y, in un punto diverso da 0)

![]()
![]()
![]() Ricorda
Ricorda
![]()
![]()
![]()
Bisettrice = retta che divide a metà un quadrante del piano cartesiano
Bisettrice del I e III quadrante: y =x
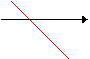
Bisettrice del II e IV quadrante : y = -x
Rette particolari: x=0 coincide con l'asse delle y
Y=0 coincide con l'asse delle x
L'equazione della retta si esprime anche in un altro modo:
ax+by+c=0 in cui a,b,c sono numeri reali
b y= - a x - c
![]()
![]()
![]()
![]()
![]() y= - a/b x - c/b m= -a/b m= y / x
y= - a/b x - c/b m= -a/b m= y / x
q= - c/b
se due rette sono parallele:
m1 = m2
![]() q1 = q2
q1 = q2
se due rette sono perpendicolari:
m1 = -1/m2
le due rette sono coincidenti (cioè sovrapposte) se :
m1 = m2
q1 = q2
calcolare la distanza fra due punti del piano cartesiano
A (x;y) B (z;k)
D= (x-z)2 + (y-k)2
calcolare il punto medio di un segmento con estremi A (x;y) e B (z;k)
M= (x+z)/2 ; (y+k)/2
calcolare l'equazione di una retta dati due punti appartenenti:
A (x;y) B (z;k)
y-k =m (x-z) oppure (g-x) / (z-x) = (n-y) / (k-y) di cui g =x dell'equazione e n= y dell'equazione
quindi l'eq. = n =g+q*
*ovviamente q non è sempre presente, dipende dalla retta
trovare il fascio proprio di rette:
C= centro del fascio = (z;k)
![]() y-z = m (x-k) formula per trovare l'equazione dl fascio
y-z = m (x-k) formula per trovare l'equazione dl fascio
retta orizzontale: m=0
retta verticale: x-z=0
calcolare il centro data l'equazione del fascio: tx-y+t-2=0
attribuisco due valori dievrsi a t e ottengo due equazioni diverse che indicano due rette apparteneti al fascio, ponendole in sistema ottengo la loro intersezione, cioè il centro del fascio
esempio: t=1 e t=0
![]() x-y+1-2=0 y=x-1 -2=x-1 x=2-1=1
x-y+1-2=0 y=x-1 -2=x-1 x=2-1=1
0-y+0-2=0 y=-2 y= -2 y= -2
C(1;-2)
formule ausiliarie:
area del triangolo con la matrice, dati i tre vertici:
A(x;y) B(z;k) C(g;n)
![]()
![]()
![]()
![]()
![]()
![]()
![]() x y 1 costruisci una tabella
come rappresentata in cui in ogni linea scrivi la coordinate di un
x y 1 costruisci una tabella
come rappresentata in cui in ogni linea scrivi la coordinate di un
![]() z k 1 punto e un uno al
fondo. Ripeti le prime due righe al fondo della tabella.
z k 1 punto e un uno al
fondo. Ripeti le prime due righe al fondo della tabella.
![]()
![]() g n 1 adesso bisogna
eseguire una serie di moltiplicazioni, anteponendo il segno del lato
g n 1 adesso bisogna
eseguire una serie di moltiplicazioni, anteponendo il segno del lato
x y 1 da cui si parte e procedendo diagonalmente come indicato dalle linee.
z k 1
risoluzione: +(x k 1) + (z n 1) + (g y 1) - (1 k g ) - (1 n x) - (1 y z)= determinante dell'area
area = determinante / 2
N.B. il determinante lo pongo sempre positivo dividendo per due perché non esistono aree negative
(ovviamente dove fra due incognite o cifre non vi è interposto nessun segno si sottintende una moltiplicazione)
baricentro di un triangolo dati i tre estremi
A (x;y) B (z;k) C (g;n)
Baricentro = G= (x+z+g) / 3 ; (y+k+n) / 3
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025