Analisi e risoluzione grafica di una relazione goniometrica

matematica

Analisi e risoluzione grafica di una relazione goniometrica

Si prenda in esempio la relazione

   ha senso per i valori di x compresi tra 0 e

Come si nota questa è una uguaglianza che presenta altre all'incognita un parametro;

sviluppandola si giunge a

La (1) perché sia compatibile con l'uguaglianza di partenza va posta a sistema con le condizioni.

Arrivati a questo punto si 252h71c potrebbe risolvere l'equazione per poi discuter i valori che il parametro deve assumere perché le soluzioni siano valide; in alternativa si può procedere a una discussione grafica.

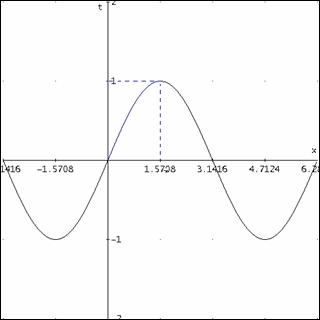
Sostituendo sin x = t e sapendo che se x deve essere compreso tra 0 e  t assume valori che vanno da 0 a1 come si può notare anche dal grafico in figura; dal sistema precedente, dunque, si passa

Se si procede a sostituire t²=y si ottiene il sistema seguente

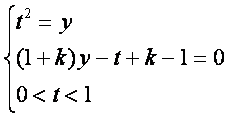
Si noti come ora nel sistema compaiano l'equazione di una parabola () e quella di un fascio proprio di rette ) che se rappresentati possono gia dare un'idea di quali possano essere le soluzioni del problema in questione.

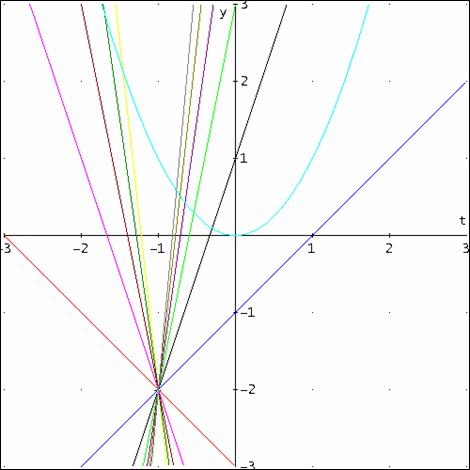
Va precisato che t deve essere compreso tra 0 e 1 quindi vanno considerata la sezione della parabola con t compreso nell'intervallo citato. (la sezione di parabola e il tratto continuo rappresentato in fig.)

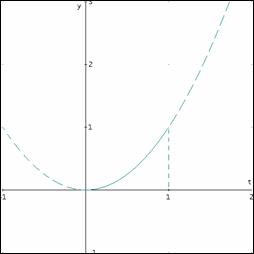Ora si capisce come perchè sia valida la relazione di partenza come soluzioni si devono prendere unicamente le intersezioni con l'arco di parabola con le rette del fascio.

Le rette che intersecano l'arco di parabola possono essere incidenti in un unico punto, tangenti, oppure secanti in due punti dell'arco.

Osservando l'intervallo delle soluzioni sarà delimitato dalle rette del fascio passanti per il punto (1;1) e l'origine che sono i punti limite dell'arco e la retta del fascio tangente l'arco.

Procedendo con i metodi noti, cioè sostituendo le coordinate dei punti (0;0) e (1;1) nell'equazione del fascio e imponendo che il discriminante dell'equazione risolvente del sistema sia uguale a zero si otterranno le seguenti rette.

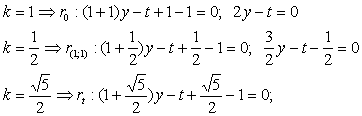
Si noti come per trovare le equazioni della retta tangente si ottengano 2 valori di k ma quello accettabile è solo quello che determina la retta tangente nell'arco di parabola in questione.

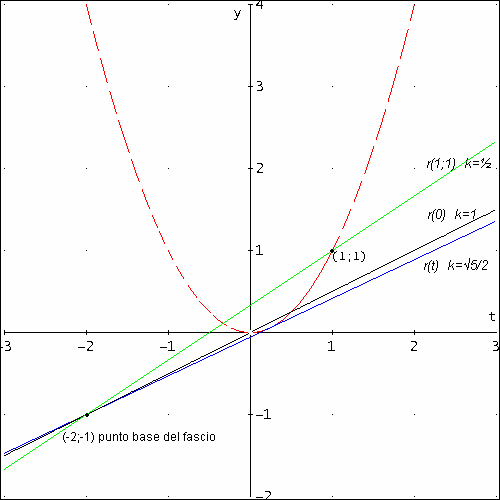
Come si deduce dalla figura ora è possibile trarre le soluzioni o comunque capirne l'andamento. Infatti si nota chiaramente che:

Per i valori di k compresi nell'intervallo  le soluzioni saranno una per ogni valore del parametro (le rette del fascio sono incidenti all'arco di parabola);

Mentre per i valori inclusi nell'intervallo 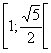le soluzioni saranno doppie e distinte per ciascun valore di k;

Per  invece le soluzioni saranno si doppie ma coincidenti.