Es. 3. Collettivo di studenti su cui rileviamo il numero di esami superati ad una certa data (disomogeneità)

Es. 4. Distribuzione della ricchezza (carattere trasferibile) in una popolazione (concentrazione)

Occorrono allora indicatori della variabilità che abbiano come obiettivo quello di quantificare il grado di dispersione di un carattere.

Esistono due criteri per misurare la dispersione

Dispersione intorno a un valore medio (m, Me, .)

Dispersione tra le diverse modalità

Nel primo caso l'indice di variabilità rappresenta una media degli scarti delle modalità osservate rispetto ad una media. L'indice più importante è certamente la varianza s di una distribuzione definita come il quadrato della media quadratica degli scarti dalla media aritmetica

In formula si ha

s S_i (x_i-m)² /n

oppure, nel caso di distribuzione per frequenze

s S_i (x_i-m)² n_i /n

Esempio: Una ginnasta è esaminata da una giuria di 5 persone e i voti che riporta (in trentesimi) sono

25 25 27 29

La media aritmetica vale m e la varianza è

Vediamo ora un esempio  con dati organizzati per frequenza.

Es. distribuzione delle partite di calcio dello scorso campionato per numero di gol segnati

La media vale

= 2.65 (m

e la varianza è

s

Proprietà della varianza

Come tutti gli indici di variabilità, s vale 0 quando tutte le unità assumono la stessa modalità.

Per un carattere trasferibile, il massimo della varianza, fissata la media, si ha quando tutte le unità assumono il valore 0 e una sola detiene il totale nm

In questo caso si ha

s m)² * (n-1)/n + (nm m)² *1/n =

m (n-1)/n +m (n-1)²/n= m n (n-1)/n=

m (n-1)

La varianza non è espressa nella stessa unità di misura delle osservazioni e per questo viene spesso preferito calcolare lo scarto quadratico medio (s.q.m.) o deviazione standard che non è altro che la radice quadrata della varianza ovvero s

La varianza o lo s.q.m. sono indici assoluti. Spesso è necessario rapportare la dispersione di un fenomeno alla sua entità media

Es.

In questo caso la varianza vale

s

Se invece

La varianza è esattamente la stessa anche se il fenomeno appare molto meno variabile .

Conviene allora considerare il Coefficiente di Variazione, definito come

C.V.=s m

che nei due casi vale, rispettivamente

e

Il C.V. può anche esprimersi come

(1/n S_i (x_i -m m )^1/2 = (1/n S_i [(x_i -m m

ovvero la media quadratica degli scarti relativi rispetto alla media aritmetica

Un metodo alternativo per calcolare la varianza

n s S_i (x_i -m S_i (x_i^2 -2x_i m m

S_i x_i^2 -2m S_i x_i + nm S_i x_i^2 -2nm +nm

S_i x_i^2 - nm da cui

s S_i x_i^2 /n - m

Un indice alternativo per la misura della dispersione è il cosiddetto scostamento semplice medio dalla mediana, definito da

S(Me)= 1/n S_i |x_i - Me|

Indici di variabilità basati sui quantili.

Così come la media aritmetica, tra gli indici di posizione può essere fuorviante in presenza di valori anomali, così la varianza può essere gonfiata da valori particolarmente distanti dalla media.

Per evitare tali inconvenienti sono stati proposti indici robusti di variabilità, tra cui ricordiamo

Range Interquartile: differenza tra il terzo  e il primo quartile (75-esimo e 25-esimo percentile)

Q₃ - Q₁

Es.: Classi di statura

Abbiamo già calcolato la mediana (Me = 172.67)

Allo stesso modo si calcolano Q₁ e Q_3.

La classe di Q₁ è [164-169) e, applicando la formula analoga a quella vista per la mediana,

Q₁=164 +(169-164)* (0.25-0.093)/(0.287-0.093)

=168.046

La classe di Q₃ è [174-179) e, analogamente,

Q₃=174 +(179-174) *(0.75-0.577)/(0.825-0.577)   =177.488

da cui discende

Q₃ - Q₁ =177.488- 168.046=9.442

Mutua variabilità

Invece di confrontare i valori della distribuzione con un indice di posizione, si possono considerare i confronti tra le diverse modalità assunte dalle unità del collettivo.

Data una distribuzione per unità di un carattere X con valori

x₁, x₂, x₃,., x_i,., x_n

si considerano tutti i confronti del tipo

| x_i- x_j| per ogni i e j=1,.,n

e se fa la media.

Si giunge così alla cosiddetta

Differenza semplice media

D S_iS_j | x_i- x_j|)/(n(n-1))

Es. Collettivo di 5 unità con valori

D

Più in generale si possono considerare differenze medie di ordine r

D_r S_iS_j | x_i- x_j|^r)/(n(n-1))^(1/r)

L'indice più utilizzato è D

Si dimostra che

La Concentrazione

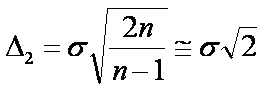
Un aspetto particolare della variabilità, specifico dei caratteri trasferibili è la concentrazione.

Consideriamo un collettivo di n unità statistiche con rispettive ricchezze (disposte in ordine crescente)

a₁, a₂, a₃,., a_i,., a_n

La ricchezza complessiva è

A_n= a₁ + a₂ + a₃ +. + a_i +. + a_n.

Se tutte le unità avessero lo stesso ammontare si avrebbe assenza di concentrazione

Se una sola unità possedesse la somma A_n e tutte le altre 0, si avrebbe la massima concentrazione.

Per analizzare situazioni intermedie consideriamo le seguenti quantità:

Per ogni i=1,.n, sia

P_i =i/n  (frazione delle i unità più povere)

Q_i =(a₁ + a₂ + a₃ +. + a_i)/A_n = A_i / A_n

(frazione di ricchezza posseduta dalle i unità più povere)

Si dimostra che, per ogni i=1,.n, risulta

P_i Q_i

Infatti,

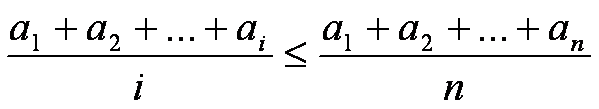
cioè  A_i / i A_n / n,  ovvero A_i / A_n i / n

Più le Q_i sono vicine alle P_i  minore è il livello di concentrazione.

Esempio (nove famiglie, redditi in milioni)

Graficamente, si ottiene la seguente spezzata che, si può dimostrare, risulta sempre convessa.

L'indice di concentrazione corrispondente fu proposto da Gini (1914) e vale

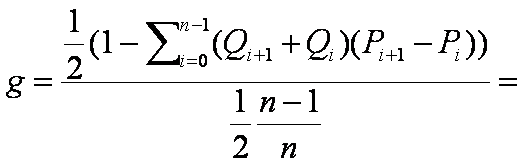
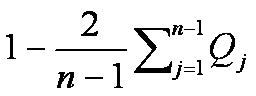
Nel nostro esempio,

g=1 -

L'Asimmetria di una distribuzione

La rappresentazione grafica delle distribuzioni può fornire informazioni cruciali sul comportamento del carattere nella popolazione in esame

Ad esempio, quando la media m coincide con la mediana Me, molto spesso questo vuol dire che la distribuzione è di tipo simmetrico unimodale (ma non necessariamente!!).

Se invece risulta Me< m gran parte delle osservazioni si posiziona su valori bassi ma alcuni valori particolarmente alti spostano la media verso destra: si parla in tal caso di asimmetria positiva

Se poi risulta Me> m gran parte delle osservazioni si posiziona su valori relativamente alti ma alcuni valori bassi spostano la media verso sinistra: si parla in tal caso di asimmetria negativa

Un primo indicatore di asimmetria

che varia tra -1 e 1.

Non è però vero che A₂ =0 implichi la simmetria.

Controesempio (pag.163. num.6.3)

Qui si ha m Me=3 ma la asimmetria è decisamente positiva.

Invece

Qui m Me=5 ma la asimmetria è decisamente negativa.

Un indice più sofisticato che risolve questi problemi è stato proposto da Fisher

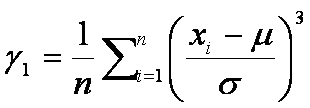
ovvero il cubo della media potenziata di ordine 3 della distribuzione standardizzata delle x_i.

Confronti tra distribuzioni: la standardizzazione.

Per poter confrontare almeno qualitativamente due distribuzioni dobbiamo eliminare i fattori che potrebbero oscurare le differenze tra le due distribuzioni.  Per questo motivo i confronti si effettuano a parità di media (convenzionalmente posta uguale a zero) e di scarto quadratico medio (posto uguale a 1) .

Questa operazione si chiama standardizzazione e consiste nel trasformare un carattere X attraverso una trasformazione lineare

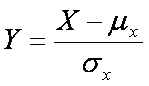
Per quanto già noto, si ottiene subito che

m_{y =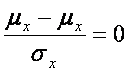}   e

s_{y =}

In tal modo i confronti fra due diverse distribuzioni vengono depurati delle eventuali differenze in posizione e variabilità