Dn,k = n (n-1) (n-2) ....... (n-k+2) (n-k+1)

Cioè

n!

Dn,k = ────

(n-k)!

PERMUTAZIONI SEMPLICI DI n OGGETTI

Si chiamano permutazioni semplici di n oggetti distinti le disposizioni semplici degli n oggetti presi a n a n. In altre parole le permutazioni di n oggetti distinti sono tutti i gruppi formati ciascuno da tutti gli n oggetti dati che differiscono fra loro soltanto per l'ordine degli oggetti.

Pn = Dn,n = n (n-1) (n-2) .... 3x2x1

Il numero delle permutazioni semplici di n oggetti distinti è uguale al prodotto dei primi n numeri naturali.

N.B.

Se K è un numero intero maggiore di uno, chiamasi FATTORIALE DEL NUMERO K, e si indica con K! il numero che risulta prodotto dei primi K numeri naturali, cioè:

K! = 1x x x x (k-1) xK

1! = 1

Se K=1 e K=0 si pone per definizione

0! = 1

Perciò possiamo dire che il numero delle permutazioni di n oggetti distinti è dato dal fattoriale del numero n, cioè:

Pn = n!

COMBINAZIONI SEMPLICI DI n OGGETTI

Si chiamano combinazioni semplici di n oggetti distinti, presi a K a K o della classe K (k≤n), tutti i gruppi di K oggetti che si possono formare con gli n oggetti dati, in modo che i gruppi differiscono tra loro almeno per un oggetto.

Evidentemente le combinazioni di classe K costituiscono una parte delle disposizioni della stessa classe.

Il numero delle combinazioni semplici di n oggetti distinti della classe K è dato da una frazione che ha per numeratore il prodotto di K numeri interi consecutivi decrescenti, il cui primo è n, e per denominatore il fattoriale di K; cioè:

n (n-1) (n-2) ... (n-k-1)

Cn,k

K!

Ora supponiamo di aver scritto tutte le combinazioni della classe K degli n oggetti dati, il cui numero indichiamo con Cn,k . Se in ciascuna di queste combinazioni permutiamo i suoi K elementi, otteniamo da ognuna di esse K! gruppi e quindi in totale avremo

Cn,k x K! = Dn,k

gruppi. I gruppi così ottenuti sono dunque disposizioni distinte, costruite con gli n oggetti dati e della classe K. Da essa segue:

Dn,k n (n-1) (n-2) ...(n-k-1)  n

Cn,k

K! K! K

Il numero delle combinazioni di n oggetti distinti della classe K è uguale al numero delle combinazioni di n oggetti della classe n-K cioè:

n n

=

k n-k

DISPOSIZIONI CON RIPETIZIONE DI n OGGETTI

Si chiamano disposizioni con ripetizioni di n oggetti di classe K con k≥n o k≤n tutti i possibili raggruppamenti che si possono formare prendendo ogni volta K oggetti con la condizione che ciascun gruppo differisca da un altro o per l'ordine in cui sono disposti gli oggetti, o per l'oggetto, o per il numero di volte in cui un oggetto viene ripetuto.

Il numero delle disposizioni con ripetizione di n oggetti di classe K è dato da n elevato alla K, e cioè:

k

D'n,k n

PERMUTAZIONI CON RIPETIZIONE DI n OGGETTI

Si chiamano permutazioni con ripetizione di n oggetti, di cui alcuni uguali fra loro, tutti i vari raggruppamenti che si possono formare con gli n oggetti, con la condizione che ogni gruppo differisca da un altro solamente per l'ordine con cui sono disposti gli oggetti.

Il numero delle permutazioni con ripetizione di n oggetti, dei quali s uguali fra loro e z pure uguali fra loro, ma diversi da s è uguale a:

s,z Dn,n n!

Pn = ────── = ──────

S Z s! Z!

Combinazioni con ripetizione di n oggetti

Si chiamano combinazioni con ripetizione di n oggetti distinti tra loro di classe k con k≤≥n, tutti i possibili raggruppamenti che si possono formare con gli n oggetti, prendendone k alla volta, con la condizione che ciascuno di essi differisca da un altro per almeno un oggetto oppure per il numero di volte con cui uno stesso oggetto può essere ripetuto.

Il numero delle combinazioni con ripetizione di n oggetti di classe k è uguale a:

n (n+1) (n+2) ..(n+k-1)

C'n,k

K (k-1) ...x x x

n+k-1

C'n,k =

K

FORMULA DEL BINOMIO DI NEWTON

n n n-k k

a+b = n a b

k=0 k

cioè:

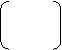n n n n-1 n n-2    2

a+b = a + a b + a b + ...

n n-1    n

....+ a b + b

n-1

I numeri

N n n ......... n n

0 1 2 ......... n-1 n

si chiamano   coefficienti binomiali.

Sulla formula    facciamo alcune osservazioni molto utili:

• Il numero degli addendi nel secondo membro della formula è evidentemente n+1
• In questi addendi gli esponenti della lettera a vanno diminuendo di una unità nel passaggio da uno qualunque o uno successivo, essendo il primo elemento a elevato alla n; mentre gli esponenti della lettera b vanno sempre aumentando di una unità nel suddetto passaggio, l'ultimo addendo essendo b elevato alla n.
• I coefficienti dei termini estremi e i coefficienti dei termini equidistanti dagli estremi sono fra loro uguali.
• Se n è dispari e quindi il numero n+1 dei termini dello sviluppo è pari, basta calcolare i primi (n+1) ∕ 2 coefficienti.
• Se invece n è pari e quindi n+1 dispari, basta calcolare i primi (n ∕ 2)+1 coefficienti.
• Il coefficiente di un termine qualunque dello sviluppo (vd. formula), a partire dal secondo, si ottiene moltiplicando il coefficiente del termine precedente per l'esponente che in esso ha la lettera a, e dividendo il risultato ottenuto per l'esponente della lettera b aumentato di una unità.

PROPRIETà DEI COEFFICIENTI BINOMIALI:

1 - Proprietà di Stirling

n n!

k =

k! (n-k)!

Il numero delle combinazioni di n oggetti di classe k è dato dal fattoriale dell'ordine fratto il prodotto tra il fattoriale della classe ed il fattoriale della differenza fra l'ordine e la classe.

2 - Proprietà dei termini complementari

n = n

k n-k

Il numero delle combinazioni semplici di n oggetti di classe k è dato dal numero di combinazioni degli stessi oggetti di classe (n-k).

3 - Proprietà di Stiegel

n = n-1 + n-1

k k k-1

La somma di due coefficienti binomiali che abbiano lo stesso ordine e classi consecutive è data da un coefficiente binomiale che ha per ordine l'ordine primitivo aumentato di 1 e per classe la classe del maggiore.

4 - Proprietà di ricorrenza

n n n-k

k+1 = k

k+1

Il numero delle combinazioni di n oggetti di classe k+1 è dato dal prodotto delle combinazioni di n oggetti di classe k per il rapporto tra la differenza fra l'ordine e la classe di tale combinazione e la classe medesima aumentata di uno.