GRANDEZZE FONDAMENTALI DELLA MATEMATICA FINANZIARIA

L'interesse viene calcolato con l'applicazione di procedimenti matematici ( REGIME DI CAPITALIZZAZIONE ) che in matematica finanziaria sono due :

Regime di capitalizzazione semplice

Regime di capitalizzazione composto

S = PRESTITO FINANZIARIO , CAPITALE IMPIEGATO

t = TEMPO

I = INTERESSE

i = TASSO DI INTERESSE

M = MONTANTE

( 1 + n i) = FATTORE I CAPITALIZZAZIONE SEMPLICE

( 1 + i ) ⁿ = FATTORE I CAPITALIZZAZIONE COMPOSTA

coppia di corte e di scadenze operazione di indebitamento

coppia di corte e di scadenze operazione di investimento

LEGGE DEGLI INTERESSI SEMPLICI

il calcolo non può superare l'anno

gli interessi via via maturati non si sommano al capitale per generare altri interessi.

L' interesse maturato viene capitalizzato ( aggiunto al capitale investito ) solo alla scadenza dell'operazione finanziaria , l'ammontare è proporzionale al capitale impiegato e alla durata dell'investimento .

Contratto di n operazioni elementari

Una operazione a pronti e (n-1) a termine

Il debito S contratto in t =0 supponiamolo rimborsabile dopo n anni

Pagamento di interesse calcolato aggiungendo ogni anno una maggiorazione costante I = i S (percentuale prefissata del debito iniziale )

Legge intertemporale descritta dalla funzione valore W ( k ) definita per k = 1 , 2 ..,

W(0) = S ,   dove: I = i * S " interesse "

W(1) = S + i S = S ( 1+ i )    i = I / S " tasso di interesse "

W(2) = S + 2 i S = S ( 1+2 i )   

W(k) = S + k i S = S ( 1+k i )

W(n) = S + n i S = S ( 1+n i )

Gli n+1 termini risultano in progressione aritmetica di ragione (i S) : In matematica, una progressione aritmetica è una successione di numeri tale che la differenza di due membri consecutivi qualsiasi è una costane. Tale differenza comune è detta ragione della progressione. Per esempio, la successione 3, 5, 7, 9, 11, ... è una progressione aritmetica di ragione 2.

W (0) = S e dopo k anni con k = 1, 2, 3 ,..n il valore dell'investimento è dato da

W(k) = S (1+ k i) con tale legge gli interessi sono sempre calcolati in proporzione al valore iniziale W ed il tasso di interesse è dato da : i _k = I / W(k - 1)

i _k = I/ S +(k - 1) I k>1 tassi a termine e solo i tasso a pronti .

M = S + I < -> S + S 525e42f i < -> S ( 1+ i ) ^"fattore di capitalizzazione semplice "

I = M - S < -> I = S ( 1+ i ) - S < -> I = S [ ( 1+ i ) - 1]

LEGGE DEGLI INTERESSI COMPOSTI

il calcolo deve superare l'anno

gli interessi si sommano al capitale e generano altri interessi a loro

Nei prestiti di lunga data si sommano gli interessi prodotti al capitale investito .

La durata del prestito viene suddivisa in sottoprestiti ( periodi di capitalizzazione ) della durata inferiore o pari ad un anno .

Al termine di ogni sottoperiodo gli interessi maturati verranno aggiunti al capitale e inizieranno a loro volta a produrre interessi .

W(0) = S , 

W(1) = S + i S = S ( 1+ i ) 

W(2) = S ( 1+ i ) + i S ( 1+ i ) = S ( 1+ i ) ²

W(k) = S ( 1+ i ) ^k-1 + i S ( 1+ i ) ^k-1 = S ( 1+ i )^k

W(n) = S ( 1+ i ) ^n-1 + i S ( 1+ i ) ^n-1 = S ( 1+ i )ⁿ

n+1 termini risultano in progressione geometrica con primo termine W(0) = S e ragione q = 1+i

una progressione geometrica è una successione di numeri tali che il quoziente di due elementi successivi della successione è una costante detta ragione della successione.

Il termine serie geometrica è riservato alla somma dei numeri di una progressione geometrica:

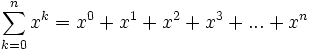
Una successione di ragione 2 e fattore di scala 1 è

M = S ( 1+ i )^{n "}fattore di capitalizzazione composta"

I = M - S

I = S ( 1+ i ) ⁿ - S < -> I = S [ ( 1+ i ) ⁿ - 1]

DEFINIZIONI FONDAMENTALI

Funzione valore : W( t ) con t 0 :è monotona crescente e rappresenta la legge di equivalenza intertemporale .

Interesse : ΔW ( t ) = W(t , t + τ) - W ( t ) è l'incremento subito dalla funzione valore .

Fattore montante

Il fattore montante o di capitalizzazione è il rapporto tra il valore nell'istante finale e quello nell'istante iniziale del periodo che va da (t, t+τ) .

Tale fattore m moltiplicato per w ( t ) ci permette di ottenere il valore a fine periodo ed essendo un rapporto tra due quantità monetarie aventi stesse dimensioni , m è una grandezza dimensionale .

Posto : t ¹= t + τ

m ( t, t+τ ) = w( t ¹)

w( t )

Fattore di sconto

Il fattore di sconto è il reciproco del fattore montante ovvero è il rapporto tra il valore nell'istante iniziale e quello nell'istante finale del periodo che va da t, t+τ ( t ¹)

Tale fattore moltiplicato per w ( t+τ ) ci permette di ottenere il valore di inizio periodo ed essendo un rapporto tra due quantità monetarie aventi stesse dimensioni , m è una grandezza dimensionale .

Posto : t ¹= t + τ

v ( t, t+τ ) = w( t )

w( t¹)

Tasso di interesse

Il tasso di interesse è il rapporto tra l'interesse maturato nel periodo e il valore nell'istante iniziale .

Essendo u rapporto tra grandezze aventi stesse dimensioni , è una grandezza adimensionale , è sempre positivo ed è espresso in termini percentuali ovvero il valore deve essere moltiplicato per 100 .

j ( t, t+τ ) = Δw ( t )

w( t )

Esprime quanto costa nel tempo un trasferimento percentuale.

In economia , il tasso (o saggio) di interesse rappresenta la misura dell'interesse su un prestito e l'importo della remunerazione spettante al prestatore .

Il debitore , infatti, ricevendo una somma di denaro, si impegna a pagare una somma superiore a quella ricevuta. Il tasso d'interesse è variabile anche in funzione della moneta di riferimento, del rischio connesso alla solvibilità del debitore e della lunghezza del periodo di riferimento.

Tasso di sconto ( tasso di interesse anticipato )

Il tasso di sconto è il rapporto tra l'interesse maturato nel periodo e il valore nell'istante finale .

Essendo u rapporto tra grandezze aventi stesse dimensioni , è una grandezza adimensionale , è sempre positivo ed è espresso in termini percentuali ovvero il valore deve essere moltiplicato per 100 .

Posto : t ¹= t + τ

d ( t, t+τ ) = Δw ( t )

w( t ¹)

Intensità di interesse

L' intensità di interesse si ha quando si rapporta il tasso di interesse alla lunghezza del periodo di riferimento (t, t+τ) , è una grandezza positiva che ha per dimensione il reciproco di un tempo es: anni^-1.

γ ( t, t+τ ) = Δw ( t )

τ w( t )

Intensità di sconto

L'intensità di sconto si ha quando si rapporta il tasso di sconto alla lunghezza del periodo di riferimento (t, t+τ) , è una grandezza positiva che ha per dimensione il reciproco di un tempo es: anni^-1.

γ ( t, t+τ ) = Δw ( t )

τ w( t )

Intensità istantanea ( forza di interesse )

Rappresenta la sensitività , cioè la sensibilità alle variazioni temporali della funzione valore . Quando τ tende a zero i tassi tendono ad annullarsi mentre le intensità tendono ad un valore unico : ( t ) = d log w ( t )

dt

lim Δw ( t ) lim Δw ( t ) w ^I(t )

τ 0 τ w( t ) 0 τ w(t +τ ) w(t)

Operazioni finanziarie

Sono operazioni finanziarie un qualunque insieme di pagamenti ( entrate - uscite ) caratterizzate dalle rispettive date di esigibilità .

Sono operazioni rappresentate da una coppia di vettori x/t₁ a m componenti reali :

x

t

Le operazioni finanziarie sono costituite dal flusso dei pagamenti x sullo scadenzario t.

Date due operazioni finanziarie x^I/ t^I x^II/t^II si definisce operazione finanziaria somma l'operazione finanziaria x/t ottenuta ridefinendo le due operazioni sullo scadenzario unione t e sommando algebricamente i pagamenti esigibili alle stesse date .

Operazioni finanziarie elementari

Si hanno quando parte e controparte stipulano un contratto finanziario caratterizzato da operazioni

di provvista ( indebitamento )

di impiego (investimento )

Il contratto stabilisce che tra i due agenti viene a crearsi una legge di equivalenza intertemporale per la quale S disponibile al tempo zero al tempo t=0 è equivalente ad S+I disponibile al tempo t=1.

Operazioni finanziarie composte

Il contratto di scambio prevede una operazione di scambio complessa ovvero la somma di operazioni elementari .

Una operazione a pronti : scambio S in t=0 con S+I in t=1

n operazioni a termine : scambio S in t=0 con S+I in t=1 e scambio S+I in t=1 con S+I+I¹ in t=2.

Due tipi fondamentali di titoli obbligazionari

Un prestito obbligazionario è una operazione di scambio monetario con le quali le aziende o istituzioni pubbliche si finanziano indebitandosi con il pubblico.

Le obbligazioni sono titoli di credito emessi sul mercato dalle società , per il procacciamento di mezzi finanziari. Sono una forma di investimento sicuro in quanto, a differenza delle azioni, chi le concede è tenuto al pagamento dell'interesse promesso anche se le sue attività sono in perdita.

L' investitore sottoscrive un numero arbitrario di contratti di obbligazioni acquistando il diritto di ricevere nel futuro un flusso di pagamenti programmato.

Molti titoli obbligazionari possono essere trattati su un mercato secondario ovvero possono essere rivenduti dall'acquirente originario ad altri investitori , i quali diventano a loro volta creditori dell'emittente per il flusso del pagamento residuo.

I titoli obbligazionari rappresentano un (debito) dell'emittente (debitore) nei confronti dell'acquirente ( creditore) ed esistono varie tipologie che si differenziano in base alla durata , alla data di scadenza e alle cedole .

In base alle cedole per esempio i principali titoli emessi dallo stato italiano sono i BOT( zero coupon bond ) e i BTP ( coupon bond ).

Titoli a cedola nulla ( titolo di puro sconto )

I titoli a cedola nulla ( zero coupon bond ) garantiscono al portatore il pagamento dell'emittente di una somma di importo fissato C ad una data futura S.

Per ricevere C ad una data futura S, l'investitore paga nell'istante corrente t un prezzo P versato in t. L' emittente garantisce al portatore del titolo il flusso di pagamenti X costituito dall'unico importo C , definito sullo scadenzario t formato dall'unica data S , detta scadenza del titolo .

L'operazione di scambio vista dall'investitore può essere sintetizzata dalle coppie di vettori:

y/s = con P , C > 0 e t < s

C = valore facciale del titolo

P = prezzo di emissione se l'obbligazione viene comprata presso l'emittente o (corso ) nel caso in

cui la transazione è effettuata nel mercato secondario

s - t = vita residua del titolo

Buoni ordinari del tesoro ( BOT )

Sono un esempio di titoli a cedola fissa emessi dallo stato italiano tramite aste di emissione che avvengono periodicamente ogni quindici giorni , sono offerti con vita e scadenza 3 , 6 e 12 mesi .

Il valore facciale del contratto elementare è cinque milioni delle vecchie lire .

w (t) = p = 5 milioni di lire

Sono tassati al momento dell'acquisto oppure alla data dei futuri pagamenti secondo una aliquota fissa ( 12, 5 % ) indipendente dalla situazione patrimoniale dell'acquirente .

Δp = Δw = C - p)

Titoli a cedola fissa

I titoli a cedola fissa garantiscono al portatore il pagamento di un flusso di pagamenti periodici ,

i primi (m-1) pagamenti sono tutti uguali ad un determinato importo I > 0 e l'ultimo pagamento è espresso da C+I con C > 0 valore facciale .

x = τ : tempo che intercorre tra un . pagamento e il successivo

t = C - p premio di emissione

y/s = / I : tasso cedolare del titolo

C

I : tasso nominale annuo

C

• P = C : titolo quotato o emesso alla pari : Un titolo è "quotato alla pari" quando il prezzo di  mercato coincide con il valore nominale o prezzo di emissione.
• P < C : titolo quotato o emesso sotto la pari : Definizione data alla quotazione di un titolo quando il prezzo di mercato è inferiore  al valore nominale.
• P > C : titolo quotato o emesso sopra la pari : Definizione data alla quotazione di un titolo quando il prezzo di mercato è superiore al valore nominale.

Rateo di interesse

Il rateo di interesse è l'importo A ottenuto moltiplicando il valore della cedola I per la frazione del periodo di godimento cedola già trascorso alla data t_i .

A = I t - t₀

t₁- t₀

dove t₀ = t₁ - τ periodo di godimento della cedola in corso

τ = t₁- t₀ tempo che intercorre tra un pagamento e il successivo

Il rateo rappresenta l'interessa maturato tra la data t₀ di inizio godimento cedola e al data di acquisto t , investendo per lo stesso periodo il capitale C secondo una legge degli interessi semplici calcolata al tasso nominale ( annuo ) del titolo . Il rateo può essere anche definito come la parte di cedola maturata fino all'istante di vendita .

A = C I (t - t₀ ) = I t - t₀

τ C   t₁- t₀

Corso tel quel : Quotazione di un titolo comprensivo dei frutti maturati dalla scadenza dell'ultima cedola al giorno di liquidazione della compravendita . Sono quotati a corso secco le azioni.

Corso secco: Quotazione di un titolo al netto dei frutti maturati dalla scadenza dell'ultima cedola al giorno di liquidazione della compravendita.
Sono quotati a corso secco i BTP, i CCT e le obbligazioni.

( Q ) è un prezzo fittizio ottenuto sottraendo il rateo dal corso tel quel "prezzo di vendita " ( P )

Q = P - A

Buoni del tesoro poliennali ( BTP )

Sono un esempio di titoli a cedola fissa emessi dallo stato italiano con scadenze di 3 , 5 , 7 e 10 anni. La periodicità di questi titoli è sempre semestrale e la cedola viene fissata dall'emittente in modo che il prezzo di aggiudicazione risulti sotto la pari , il taglio minimo è cinque milioni delle vecchie lire e anche i BTP sono tassato al 12,5 % ma in questo caso la tassa viene pagata dal detentore del titolo sottoforma di ritenuta che l'emittente effettua sull'ammontare delle poste da esso dovute quindi ogni cedola è decurtata del 12,5 % e C invece solo per il premio di emissione .

Lezione 2

TAN sta per "tasso annuale" ed è espresso in percentuale su base annuale ( regime semplice ).

TAEG sta per "tasso annuo effettivo globale" ed è espresso in termini percentuali su base annuale ( regime composto ).

Il tasso annuale è quel tasso di interesse espresso in  percentuale sul credito concesso al cliente ovvero quel tasso puro applicato al finanziamento.

Il tasso Annuo Effettivo Globale è il tasso che indica il costo complessivo di un credito - finanziamento - erogato da banche o finanziarie e quindi comprende qualsiasi spesa e costo relativi al finanziamento.

Il TAN, a differenza del TAEG, non comprende le spese accessorie che sono poi quelle che fanno lievitare il costo globale del prestito, ad es. le perizie, l'istruttoria, le spese per i bollettini postali, etc.).

NB Tutte le operazioni sono trattate in regime composto tranne il caso in cui è espressamente richiesto il regime semplice .

Tassi equivalenti secondo la legge esponenziale

Dal punto di vista pratico si pone la necessità di stabilire una regola di equivalenza tra indici finanziari ( tassi e intensità ) affinché la forza o il tasso d'interesse di una operazione finanziaria possa essere confrontata con quella di una seconda operazione .

Se facciamo riferimento alla funzione valore W ( t ) = e δ ^t e alteriamo la scala temporale moltiplicando l'unità di tempo anno per il fattore positivo ( q ) la nuova misura temporale sarà data da t ¹ = t /q e la funzione valore sarà W¹ ( t¹ ) = e δ^{1 t1}

Le operazioni quindi devono essere misurate secondo la stessa scala temporale .

• Forza di interesse = = d log w ( t )= log (1 + i)

dt

• fattore positivo = q = 1/m ( mesi )
• nuova misura temporale = t ¹= t / q
• tassi d'interesse i ¹ = ( 1 + i ) ^q
• nuova forza d'interesse = δ¹ = δ * q

Per trovare la forza di interesse equivalente la funzione espressa nelle due scale deve essere la stessa

W¹ ( t¹ ) = W ( t )

δ^{1 t1} = δ ^t cioè δ^{1 t/q} = δ ^t

δ¹ = δ * q

Per trovare il tasso equivalente deve essere soddisfatta l'uguaglianza

( 1 + i¹ ) ^t1 = ( 1 + i ) ^t

( 1 + i¹ ) ^{t /q} = ( 1 + i ) ^t per cui si ha

i¹= ( 1 + i ) ^q - 1

ESEMPIO

; t = 3 ; mesi = sottoperiodi ; i = 10% ; q = 1 / m = 1 / 12

m ( t ) = e δ ^t = e ^{0.3 * 3} = 2.459603

t ¹ = t / q = 3 * 12 = 36

Le intensità devono essere equivalenti :

* q = 0.1 * 1/ 12 = 0.0083

I tassi devono essere equivalenti :

i ¹ = ( 1 + i ) ^q - 1 = ( 1 + 0.1 )^1/2 - 1 = 0.0488 = 4.8 % 10 % e i ¹ (deve essere semestrale )

= log (1+ i) = log (1 + 0.1 ) = 0.0953

Nel regime semplice , quindi con tassi nominali le trasformazioni avverranno :

annuo mensile i / 12

mensile annuo i * 12

Passare da un tasso annuale ad un tasso bimestrale

( 1 + i ) ¹ = ( 1 + i ) ⁶ " equivalenza tra i due tassi annuale e bimestrale"

( 1 + i ) ^{1 / 6} = ( 1 + i ) ^{6 / 6} quindi i¹ = ( 1 + i ) ^{1 / 6} - 1

Valore di una operazione finanziaria in base alla legge esponenziale

Supposta una operazione finanziaria x /t caratterizzata dai vettori degli importi e dei tempi

x_{k =} posta

VALORE DEL FATTORE ATTUALE

Se consideriamo l'istante zero come l'istante corrente e consideriamo una legge esponenziale con intensità il valore attuale lo indicheremo V( t , X ) : è la somma di denaro , che in condizione di equità , può oggi essere scambiata con una somma che sarà invece disponibile in una data futura .

W( 0 , X _k ) = x_k e -δ ^{t k}    per k = 1 , 2 ,..,m

Quindi il valore attuale si ha moltiplicando il fattore di sconto e -δ ^{t k} per la somma x_k.

La somma dei valori attuali è data da : per t>0

V( t , X ) = W ( 0 , X _k ) cioè

V( t , X ) = x_k e -δ ^{t k} = x_k ( 1+ i ) ^{t k}

VALORE DEL FATTORE MONTANTE ( di sconto )

Se consideriamo l'istante finale X come l'istante corrente e consideriamo una legge esponenziale con intensità , il valore montante lo indicheremo M (t , X ): è la somma di denaro , che in condizione di equità , sarà data a colui che ha impiegato una somma di denaro in epoca antecedente e con valore sicuramente minore S . In altri termini ci dice il flusso x in t quanto vale .

W( t , X _k) = W ( 0 , X ) e δ ^t

Nelle stesse ipotesi : per t>0

M( t , X ) = W ( 0 , X ) e δ ^t = x_k ( 1+ i ) ^t

FORMULA GENERICA

W( t , X_k) = (m) e δ ^{( t - tk )} = X_k ( 1+ i ) ^{t - tk}

In sintesi :

Fattore attuale W( 0 , X _K ) = x_k e -δ ^{t k}

Fattore attuale W( 0 , X _K ) = x_k e δ ^t

montante__________tk < t_______________t__________tk > t____________flusso residuo

X _K e -δ ^{t k} e δ ^t

M( t , X ) = X _K e δ ^{( t - t k )} con ^{t k < t}

V( t , X ) = X _K e δ ^{( t k - t )} con ^{t k > t}

W( t , X ) = M( t , X )+ V( t , X ) = montante + valore residuo

Operazioni finanziarie eque

Le operazioni finanziarie sono eque solo e soltanto per tasso e forza di interessi espressi in regime composto .

W( t , X )= 0

M( t , X )= - V( t , X )

Una qualunque operazione finanziaria si dice equa , al tempo t , quando il valore delle somme incassate è uguale al valore delle somme pagate e per essere equa almeno un importo deve avere segno diverso dagli altri .

Proprietà funzionali della legge esponenziale

Proprietà invariantiva : se una operazione finanziaria è equa in un istante t secondo una assegnata legge esponenziale , lo è in qualsiasi altro istante .

Proprietà additiva : se due operazioni finanziarie sono eque in un medesimo istante , conformemente ad una stessa legge esponenziale , anche l'operazione finanziaria somma è equa allo stesso istante , secondo la stessa legge esponenziale .

Proprietà di uniformità nel tempo : se una operazione finanziaria è equa all'istante t secondo una assegnata legge esponenziale , l'operazione avente tutte le scadenze traslate di un intervallo di lunghezza è equa nell'istante t + τ conformemente alla stessa legge

Proprietà di scindibilità : La somma di due operazioni finanziarie eque in due istanti diversi secondo una medesima legge esponenziale , è un' operazione equa , secondo la stessa legge esponenziale , in un qualsiasi istante . ( proprietà invariantiva + proprietà additiva )

t_{0_____ _______ ______ ______________}t_{_1__________ ______ ____ __}t₂

"Equazione funzionale della scindibilità" esprime una proprietà dei fattori di sconto

t₀ t_{_1} t₂

v(t_1- t₀) ₌ v(t_1- t₀) v(t_{2 -} t₀)

v( t_{0 ,} t₁ ) ₌ v( t_0, t_1-) v(t_1,t₂ )

Dalla proprietà di uniformità nel tempo deriva

t , t^I = t + τ con τ > 0

t t^I

v(t _, t₁) ₌ v(τ) si può asserire che il fattore di sconto dipenda da τ e non da t^I e t.

t_1- t₀ = τ^I

t_2- t₁=τ^II

v(τ^I - τ^II ) = v(τ^I ) v(τ^II )

v(τ) = e -δ ^t v(0) = 1

Determinazione nello specifico del montante

X₀_________X₁__________X_₂______________X__m    t _k = 1, 2, 3 ,. .., m

t₀ t₁ t _k t₂ t_m

Verificare come varia il montante ovvero il suo aspetto dinamico .

M( t _k , X ) = M_K Per comodità di scrittura

M_K = X _h e δ ^{( t k - t h )} con h t k e xk =posta

Esempio : Con t k = 6

_______10_______20_____30__________40__________50

0 2 5 6 9 12

M ₆ = 10 e δ ^{( 6 - 2 )} + 20 e δ ^{( 6 - 5 )} + 30 e δ ^{( 6 - 6 )}

Essendo l'ultimo termine nullo mi serve prendere i termini fino a X k -1

M_K = X _k + M_K-1 e δ ^{( t k - t h )} e δ ^{( t k - 1 ) "}sino alla posta immediatamente

e δ ^{( t k - 1 )} precedente a k

M_K X _k X _h e δ ^{t k} e - δ ^{t h} e δ ^{t k -1} e - δ ^{t k-1} con h t k-1

M_K = X _k + e δ ^{t k} e - δ ^{t k -1} X _h e δ ^{t k -1} e - δ ^{t h}

M_K = X _k + e δ ^{( t k - t k - 1 )} X _h e δ ^{( t k -1 - t h)}

M_K = e δ ^{( t k - t k 1 )} M_K-1 + X _k con k = 1, 2, 3 , .., m

0 3 7 12 18 20 24

M₁₂= 20 + M _{7 +} (1+i ) ⁵; M₇ = 10 + M ₃ +(1+i ) ⁴ ; M₂₄ = 40 + M₂₀ + (1+i ) ⁴

Lezione 3

DEFINIZIONI PRELIMINARI

Definizione di rendita

La rendita è una tipologia di operazione finanziaria r complessa , costituita da una successione di somme di segno uguale ( pagamenti ), esigibili o pagabili a determinate scadenze .

Le somme sono chiamate rate o termini , mentre il lasso di tempo prende il nome di periodo .

RENDITE:

Periodiche ampiezza del periodo costante es. ( anni - mesi )

Non periodiche ampiezza del periodo variabile

A rata costante importi uguali

A rata variabile rate differenti

Temporanee n° finito di rate

Perpetue n° illimitato di rate

Immediate Se la prima rata viene riscossa (o pagata) da subito t = 0

Differite Se la prima rata viene riscossa (o pagata) a cominciare da un certo istante successivo a e

Anticipate se t₀ = t₁ Se la scadenza è fissata all'inizio di un intervallo di tempo

Posticipate se t₀ = t_1-1 Se la scadenza è fissata al termine di un intervallo di tempo

Certe Non condizionate da avvenimenti

Aleatorie Condizionate da avvenimenti

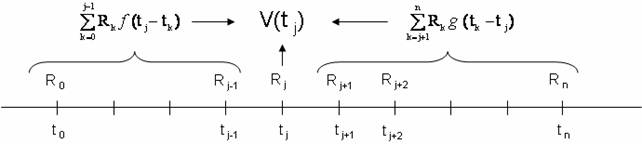
Valore di una rendita

Il valore di una rendita finanziaria all'istante è la somma dei montanti delle rate con scadenze antecedenti a , dei valori attuali delle rate con scadenze successive a , ed eventualmente della rata con scadenza

Valore attuale di una rendita

Il valore attuale di una rendita è il valore calcolato al tempo ed equivale alla somma dei valori attuali delle singole rate della rendita nel regime di capitalizzazione prescelto.

Valuteremo il valore attuale della rendita in base ad una assegnata legge esponenziale ovvero bisognerà applicare i concetti appresi con lo studio della legge esponenziale .

La situazione più semplice è quella quando tutte le rate hanno eguale valore e quindi ci troviamo di fronte a rendite a rate costanti .

Montante di una rendita

Il montante di una rendita è il valore calcolato al tempo ed equivale alla somma dei montanti delle singole rate calcolati al termine della rendita nel regime di capitalizzazione prescelto.

RENDITA IMMEDIATA POSTICIPATA DI DURATA m

Tale rendita r è composta da :

numero m finito di rate

data di inizio in zero t =0

prima rata pagabile alla fine del periodo ( primo anno ) t₁= t₀+1

X_k = R ( RATA ) ; t _k = k , k = 1, 2 ,.m

Se prendiamo in considerazione le rendite immediate posticipate a rate costanti ci troviamo di fronte a tele situazione :

__________R_______R__________R_________________R

1 3 4 m

Il problema è determinare il valore della rendita in ogni istante di tempo .

Valore attuale è la somma dei valori attuali di tutte le poste e per calcolarlo necessito o di una forza d interesse oppure di un tasso di interesse .

1 2 3..........m

Per facilità di calcoli consideriamo R = 1 "unitario"

v = ( 1+ i ) ^-1  v ragione della progressione geometrica

V ( 0 , r ) = ( 1+ i ) ^-1 + ( 1+ i ) ^{- 2} + ( 1+ i ) ^{- 3} +...+ ( 1+ i ) ^{- m}

v + v² + v³ +..+ v ^m   S _N = a 1 - q ^m / 1 - q se q < 1

V ( 0 , r ) = v ^K Per k che va da 1 a m

V ( 0 , r ) = R v 1 - v ^m V ( 0 , r ) = R ( 1+ i ) ^-1 1 - ( 1+ i ) ^{- m}

1 - v 1 - ( 1+ i ) ^{- 1}

V ( 0 , r ) = R 1 - ( 1+ i ) ^{- m} infine il valore attuale della rendita in esame è:

i

V ( 0 , r ) = R 1 - v ^m = " calcoliamo la rendita nell'istante 0"

i

i * + v ^m = 1 unità monetaria

dove v ^m è il fattore di sconto di una unità monetaria che scade in m ricondotta in zero e è il valore attuale e quindi scambio l'operazione con una unità monetaria .

NB L'operazione per essere equa lo scambio deve essere alla pari .

Valore montante è la somma dei valori montanti di tutte le poste e per calcolarlo necessito o di una forza d interesse oppure di un tasso di interesse.

u = ( 1+ i )    u ragione della progressione geometrica

M ( m , r ) = 1* u ⁰ +1*u ¹ + 1*u ² + 1*u ³+...+ 1*u ^m-1 S _N = a q ^m-1 / q - 1

M ( m , r ) = u ^{K -1} Per k che va da 1 a m

M ( m , r ) = R* u ^m- 1 = "calcoliamo la rendita nell'istante m"

i

RENDITA IMMEDIATA ANTICIPATA DI DURATA m

Tale rendita r è composta da :

numero m finito di rate

data di inizio in zero t =0

prima rata pagata immediatamente t₁= t₀

X_k = R ( RATA ) ; t _k = k - 1 , k = 1, 2 ,.m

1_______1_________1_________1_________1

0 1 2 n-1 n

Valore attuale

V ( 0 , r ) = v⁰ + v¹ + v² + v³ +..+ v ^n-1

V ( 0 , r ) = v ^K-1 Per k che va da 1 a n

V ( 0 , r ) = R 1 - v ^m R 1 - v ^m = ^"calcoliamo la rendita nell'istante 0"

1 - v  d

Valore montante

M ( m , r ) = v¹ + v² + v³ +..+ v ^m

M ( m , r ) = u ^K Per k che va da 1 a m

M ( m , r ) = R u u ^m- 1 = "calcoliamo la rendita nell'istante m"

i

RENDITA PERPETUA POSTICIPATA

"con R = 1 unitario"

1 2

Tale rendita è detta perpetua perché il valore montante è indeterminabile in quanto la scala temporale tende ad infinito ( ) e inoltre è posticipata perché la scadenza è fissata al termine dell'intervallo di tempo e quindi prima rata pagabile alla fine del periodo ( primo anno ) t₁= t₀+1.

Calcolo del valore attuale:

• v + v² + ...+ v ∞ è una serie geometrica di ragione v convergente perché la ragione

è minore di uno .

• W ( 0, r ) = lim R v ^k = R v ^k " Per K che va da 1 a ∞

m

W ( 0, r ) = R v 1 - v = R v _ = R v _ = [ R/ i ]

1 - v 1- v v i

Un esempio di rendita perpetua potrebbe essere in linea di principio la pensione oppure la rendita di un immobile .

In letteratura :

RENDITA PERPETUA ANTICIPATA

1_________1________1_____________1 "con R = 1 unitario"

0 1 2

Tale rendita è detta perpetua perché il valore montante è indeterminabile in quanto la scala temporale tende ad infinito ( ) e inoltre è anticipata perché la scadenza è fissata all'inizio dell'intervallo di tempo e quindi prima rata pagata all' inizio del periodo ( primo anno ) t₁= t₀.

Il valore di tale rendita si può calcolare capitalizzando per un anno il valore della corrispondente rendita posticipata ovvero :

W ( 0, r ) = 1/v * R/ i = [R/d]

Oppure si può calcolare tramite il calcolo del valore attuale sviluppando la serie geometrica.

Calcolo del valore attuale:

v ⁰ + v¹ + ...+ v ∞

• W ( 0, r ) lim R v ^{k -1} = R v ^k " Per K che va da 1 a ∞

m

W ( 0, r ) = v ^k v ^-1 v ^-1 R v ^k v ^-1 R / i

W ( 0, r ) = 1/v * R/ i = [R/d]

In letteratura :

RENDITA DIFFERITA DI n ANNI

________________R_______R__________R "Da o a n si ha un intervallo vuoto"

0 n n+1 n+2..... n +m "X_k =R ; t_k = k + n , k=1,2,..,m

Se n > o allora la rendita è differita nel tempo e quindi per il calcolo del valore attuale trovo il valore della rendita immediata "valore in n" e poi lo porto in zero scontandolo .Quindi si possono considerare le rendite immediate come casi particolari delle rendite differite ( n =0 )

W ( 0, r ) = v ⁿ⁺¹+ v ⁿ⁺²+..+ v ^{n + m}

W ( 0, r ) = R v ^{k + n} "Per k che va da 1 a m "

W ( 0, r ) = R v ⁿ v ^k "Per k che va da 1 a m "

W ( 0, r ) = R v ⁿ⁺¹ 1 - v ^m

1 - v

W ( 0, r ) = R v ⁿ 1 - v ^m " Fattore di sconto per valore attuale"

i

In letteratura :

W ( 0, r ) = R v ⁿ a n i W ( 0, r ) = R _n a m i

RENDITA FRAZIONATA

R_r__r__r__R_r__r___r__R_r___r___r__R

0 1 2 n

Le rendite frazionate sono il caso più rilevante nella pratica ovvero rendite con pagamento delle rate su periodi più brevi di un anno .

Per calcolare il valore della rendita bisognerà suddividere gli intervalli temporali e al posto di versare la rata R alla fine di ciascun periodo ( anno ) bisognerà versare un n-esimo alla fine di ciascun n-esimo anno .

• R'= R/n rata
• n m = durata
• i/n = periodicità
• t' = n t   nuova scala temporale
• q = 1/n fattore di scala
• i'= ( 1 + i )^q - 1
• v' = v ^1/n
• δ' = δ / n

Il valore attuale della rendita frazionata espresso nelle due differenti scale sarà dato :

W ( 0, r _n ) = R' (v')^k "Per k che va da 1 a n m"

W ( 0, r _n ) = R' v' 1 - (v') ^nm " 1- v' = v' i' (tasso di sconto)"

1 - v'

W ( 0, r _n ) = R' v' 1 - (v') ^nm " semplifico v' "

v' i'

W ( 0, r _n ) = R' 1 - (v') ^nm

i'

W ( 0, r _n ) = R' 1 - (v^1/n) ^nm i / i " semplifico n e divido e moltiplico per i"

i'

W ( 0, r _n ) = R 1 - v^m i / n i' " i / n i' prende il nome di fattore di correzione "

i

Lezione 4

DEFINIZIONE DI OPERAZIONE DI RENDITA

+S_____-R_____-R______-R______-R

0 1 2 3 n

L'operazione di rendita è una operazione finanziaria che prevede lo scambio di una grandezza monetaria S,versata al tempo zero , con una successiva rendita r avente rate R di segno opposto. La grandezza monetaria di segno opposto deve essere definita in un periodo "minore - uguale" al momento del pagamento della prima rata .

Le rendite che analizzeremo per le nostre operazioni di rendita saranno la rendita immediata e la rendita differita entrambe sia anticipate che posticipate e quindi ci sarà lo scambio di una grandezza monetaria con una di queste rendite.

L'operazione di rendita avviene tra la parte che paga S per poi ricevere le rate della rendita e la controparte che contrae un debito ricevendo S in zero per poi ammortizzarlo tramite il pagamento di un numero di rate di importo prefissato .

Per la parte l'operazione di rendita prende il nome di operazione di investimento.

Per la controparte l'operazione di rendita prende il nome di operazione di ammortamento .

Di una operazione di rendita è molto importante conoscere l'evoluzione temporale ovvero conoscere il montante e il valore residuo M_K e V_K nel loro aspetto dinamico .

Analizziamo:

rendita r immediata posticipata con m rate R_K

operazione di scambio x = /

x₀ = S e x_k = - R_{K ,} t_k = k per k che va da 1 , 2 ,..,m

x₀ = +S__________ ______ ____ _______ x_k = - R _k

0 t₁ t₂............t_m

L' operazione di rendita viste dalla controparte consiste nell'incassare al tempo zero S per poi pagare successivamente la rendita r assegnata una legge esponenziale di tasso annuo i .

MONTANTE

Il montante dell'operazione di rendita , a ciascuna data , è la somma dei montanti di tutte le somme pagate fino a quella data .

M_K = x_h ( 1 + i )^{k - h} " Per h che va da 0 a k"

M_K = S ( 1+ i )^k - R_h ( 1+ i )^{k- h} k = 0, 1 , ..m.

VALORE RESIDUO

Il valore residuo dell'operazione di rendita , a ciascuna data , è il valore scontato delle somme future .

V_K = - R_h ( 1+ i ) ^{- (h - k)} "Per h che va da k + 1 a m"

VALORE COMPLESSIVO

Ad ogni istante k la somma del montante e del valore residuo fornisce il valore complessivo dell'operazione di rendita

W( k, x ) = M_K + V_K

Il montante M_K rappresenta il debito residuo all'istante k , cioè il debito non ancora pagato che resta da estinguere a quella data ; non assume mai valori negativi e si annulla solo alla scadenza m.

Il valore residuo V_K rappresenta il bilancio finanziario al tempo k sempre negativo per k< m e nullo solo al rimborso completato .

M_K = - R _k + ( 1+ i ) M_K-1 k = 1 , 2 ,..,m

M₀ = S

Descrive l'evoluzione del montante evidenziando le variazioni dovuta all'accumularsi degli interessi e al pagamento delle rate.

SCAMBIO CON RENDITA IMMEDIATA POSTICIPATA

M₀ = S = - V₀

M₁ = M₀+ i M₀ - R M₀( 1+ i ) - R = - V₁

M₂= M₁+ i M₁ - R M₁( 1+ i ) - R = - V₂

M_k = M_{k -1}+ i M_k-1 - R M_{k -1}( 1+ i ) - R = - V_k

M_m = M_{m -1}+ i M_{m -1} - R M_{m -1}( 1+ i ) - R = - V_m

La prima parte della tabella non è altro che lo sviluppo della formula:

M_K = - R _k + ( 1+ i ) M_K-1 k = 1 , 2 ,..,m .

Il debito residuo si ottiene aggiungendo al debito residuo dell'anno prevedente M_K-1

gli interessi annui e detraendo la rata R.

Calcolo della rata

M_K = M_{k -1}+ i M_k-1 - R

R = (M_{k -1} -M_K) + i M_k-1 k = 1 , 2 ,..,m .

Ogni rata risulta scomposta in una quota di capitale:

C_K = (M_{k -1} -M_K)

E in una quota di interesse :

I_K = i M_{k -1}

La quota capitale è destinata all'estinzione del debito mentre la quota di interesse è destinata al pagamento degli interessi dovuti per il prolungamento di un anno della situazione di indebitamento .

Mentre la quota di interesse tende a zero , la quota capitale aumenta per far sì che la rata sia costante.

C_K = (M_{k -1} -M_K) = M₀ -M_m = S - M_m " Per k che va da 1 a m"

C_K = S Perché la condizione di chiusura è M_{m =} 0 la somma delle quota di capitale devono coincidere con il debito da rimborsare .

Dimostrazione

C_K+1= M_k - M_K+1 = [M_k-1( 1+ i ) - R] - [M_k( 1+ i ) - R]

C_K+1= M_k-1( 1+ i ) -R - M_k( 1+ i ) +R

C_K+1= M_k-1+ i M_k-1- M_k - i M_k

C_K+1= M_k-1- M_k + i (M_k-1- M_k)

C_K+1= C_K + i C_K

C_K+1= C_K( 1+ i )

le quote capitale della rendita a rata costante risultano in progressione geometrica di ragione ( 1+ i ) e primo termine C_1.

C₁= M₀ - M₀( 1+ i ) + R R - i M₀ R - i R 1- v ^m/ i

C₁ = R - i M₀

C₁= R - i R 1- v ^m

i

C₁ = R ( 1- 1 + v ^m) R v ^m

C₁ = R v ^{m - 1 + 1}

C₂ = R v ^{m - 2 + 1}

C₃ = R v ^{m - 3 + 1}

C_k = R v ^{m - k + 1}

Le quote di interesse saranno:

I_K = R - C_k

I_K = R- R v ^{m - k + 1}

I_K = R ( 1 - v ^{m - k + 1} )

Conoscendo la rata posso determinare tutti i debiti residui , tutte le quote capitale e le quote interesse .