|
|
| |
Funzione primitiva
Definizione: Si dice che F è una primitiva di f se:
F' (x) = f (x)
F (x) = 1 → F (x) = x
f (x) = 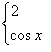
![]() → F (x) =
→ F (x) = ![]()
Oss. Se una unzione f è definita con più leggi assegnate su intervalli disgiunti, allora la primitiva si ottiene calcolando la primitiva di ciascun ramo
ATTENZIONE: se gli intervalli non 323b15d fossero disgiunti
F' (x) =f (x) =![]() → F (x) =
→ F (x) = ![]()
Limiti delle derivate
![]() F'(x) =
F'(x) = ![]() 1 = 1
1 = 1
Non è derivabile in 0, perché non è continua e perché i limiti
delle derivate sono diversi
![]() F'(x) =
F'(x) = ![]() 2 = 2
2 = 2
Oss. Per costruire la primitiva in un certo intervallo, occorre che f sia continua nello stesso.
Teorema
Esistono infinite primitive di una assegnata funzione
f (x) = 1 → F (x) = x + k (con k = costante)
f (x) = ![]() F (x) =
F (x) = 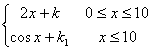
K può assumere qualsiasi valore diverso per i 2 rami.
Teorema
Se F e G son due primitive di f in un intervallo, allora differiscono per una costante, cioè:
F (x) = G (x) + k
Dimostrazione:
D (F -G) = DF - DG = f -f = 0 (in tutto l'intervallo poiché F e G della stessa funzione f)
F'= f G'= f
Poiché la derivata di F-G = 0 nell'intervallo la funzione F - G deve essere costante, quindi:
F - G = K
Integrale indefinito
Def. Si dice integrale indefinito di f e si indica con:
![]() dx
dx
Ed è l'insieme di tutte le primitive.
Primitive di f(x)
|
f (x) |
P f(x) |
|
|
k |
|
x |
|
|
|
log │x│ |
|
|
|
|
sen x |
-cos x |
|
cos x |
sen x |
Regola di scomposizione
P ( f ![]() g ) = P f
g ) = P f ![]() Pg
Pg
P ( k * f ) = k Pf
Calcolare l'integrale indefinite di:
![]() dx =
dx = ![]()
![]() + x + k
+ x + k
P = ![]() =
P
=
P 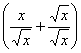 = P
= P 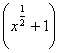 =
P
=
P ![]() + P
+ P ![]()
![]()
![]()
![]()
![]()
![]() =
=
![]() =
=
![]() =
=
![]()
![]() =
=
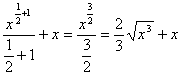
Regole di integrazione per parti
P (f*g) = Pf * g - P (Pf * g') Derivando deve essere = 0
Dimostrazione
Per dimostrare la formula deriverò l'equazione a destra per mostrare che tale
derivata è uguale a ( f * g).
D ![]() =
=
D ![]()
Oss. DPf = f
Derivata della primitiva di f = f
Richiamo
Primitive per scomposizione
Primitive di prodotto (integrazione per parti)
ESERCITAZIONE SULL'INTEGRAZIONE PER PARTI
Calcolare il seguente integrale:
![]() x sen x dx
x sen x dx
↓
g f
Applico la formula:
P f = - cos x
g
(Pf) * g - P ( Pf g')
cos x * x - P ( -cosx * 1) = (Applico la regolaq sopraindicata in b, 1 è k cioè una costante)
= - x cos x + P (cos x) = x cos x + senx + k
NB = D Pf = f
Esercizio:
Calocolare il seguente integrale
![]() dx =
dx = ![]() 1 logx
1 logx
E' una forma elementare, se la derivo è calcolabile facilmente, dobbiamo pensare di riscrivere la funzione come 1 * f
Quindi:
![]() 1 * log x = applico la formula dell'ntegrazione per parti = x
log x - P (x *
1 * log x = applico la formula dell'ntegrazione per parti = x
log x - P (x * ![]() ) = x log x - P (1)
) = x log x - P (1)
↓ ↓ ↓ ↓ ↓ ↓
f g Pf g Pf g'
Primitiva per sostituzione e primitiva di una funzione composta
Px f ( g
(x) ) = Pt ( f (t) * ![]() (t) )
(t) )
t =g (x)
x = ![]() (t)
(t)
dx
= ![]() (t) * dt
(t) * dt
![]() f (x) dx = F (x) + k
f (x) dx = F (x) + k
F' (x) = f (x)
D F (x) = f (x) * dx
ESEMPIO
![]() ( 3x +2)³ dx
( 3x +2)³ dx
Facciamo la sostituzione:
![]() (3x +
2) ³ dx =
(3x +
2) ³ dx = ![]() t ³
t ³ ![]() dt =
dt = ![]()
![]() t³ dt
t³ dt ![]() *
* ![]() + k
+ k
↓
3x + 2 = t³
g (x) = 3x + 2
f ( g (x) ) = (3x + 2 )³
Calcolo il differenziale:
![]()
![]()
1 dx = ![]() → 1 dx =
→ 1 dx = ![]() dt
dt
Ricordiamo che = 3x + 2 e avremo quindi:
![]()
ESERCIZIO
![]()
↓
f (t) = sen t t = -x+2 = g(x)
t = -x+2 → x = t+2
g (x) =
-x+2 x = -t +2 = g![]() (t)
(t)
dx = -dt
![]() dt =
dt =
![]() sostituisco t = -x+2 = cos (-x+2) + k
sostituisco t = -x+2 = cos (-x+2) + k
ALTRO METODO PER PRESENTARE LA REGOLA
Regola per sostituzione, supponiamo di over calcolare:
![]()
↓
t = g (x)
dt = g' (x) dx
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025