|
|
| |
Integrale
In analisi matematica: A) i. definito di una funzione f(x) è il valore numerico espresso dal simbolo
![]() _[1v\h8"f12_84.wmf"_[0v
_[1v\h8"f12_84.wmf"_[0v
i. indefinito di una funzione f(x) è ogni funzione la cui derivata sia f(x). B) Data un'equazione differenziale del tipo y =F(x,y,y ), viene definito i. primo ogni relazione del tipo f(x,y,y )=costante che sia identicamente soddisfatta da ogni soluzione y dell'equazione differenziale data. Il concetto si generalizza a sistemi di equazioni differenziali e trova applicazioni notevoli in meccanica razionale. C) Calcolo i. è l'insieme delle regole e dei teoremi relativi al concetto di integrale. D) Equazione i., equazione nella quale le funzioni incognite figurano sotto il segno di integrale. Le più note sono le equazioni di Fredholm e di Volterra.
INTEGRALE DEFINITO
Sia y=f(x) una funzione definita e limitata nell'intervallo chiuso e limitato [a,b] dato dalle x tali che a x b; diviso questo in n intervalli di ampiezza qualunque h ,h ,...,hn, quindi Shi=b-a, si indichi con fi un qualunque valore di f(x) nell'i-mo di questi; si moltiplichi ciascun fi per l'ampiezza hi dell'intervallo a cui appartiene e si considerino le somme
![]() _[1v\h8"f12_85.wmf"_[0v
_[1v\h8"f12_85.wmf"_[0v
Se al tendere a zero della massima ampiezza delle parti hi esiste il limite delle somme S, la f(x)
si dice integrabile nell'intervallo [a,b]; il limite stesso viene
detto i. definito di f(x) in [a,b] e lo si
rappresenta con il seguente simbolo![]() _[1v\h8"f12_86.wmf"_[0v
_[1v\h8"f12_86.wmf"_[0v
dove i numeri a e b sono i limiti di integrazione, f(x) è la funzione integranda, x è la variabile di integrazione; il simbolo è una deformazione della lettera S, iniziale della parola somma; l'i. così come è stato definito è detto i. secondo Riemann, o anche i. secondo Mengoli-Cauchy. Considerata la rappresentazione grafica della funzione y=f(x), si osserva che, nel caso in cui si abbia f(x) 0 per a x b, l'i. corrisponde all'area del trapezoide costituito dall'insieme dei punti del piano che soddisfano alle disuguaglianze: a x b y f(x) (fig. 1). L'operazione di integrazione si chiama anche quadratura perché l'i. definito permette di quadrare le superfici, cioè di determinarne l'area. Si può dimostrare che una condizione necessaria per l'integrabilità di una f(x) in un intervallo è che essa in tale intervallo sia limitata, ma questa è una condizione non sufficiente perché, p. es., la funzione di Dirichlet è ovunque limitata, ma non ammette integrale. Sono integrabili tutte le funzioni continue e, fra le discontinue, quelle che, essendo limitate, presentano discontinuità in un numero finito di punti, cioè le funzioni generalmente continue.
PROPRIETÀ DELL'INTEGRALE DEFINITO
Se si pone per definizione
![]() _[1v\h8"f12_87.wmf"_[0v
_[1v\h8"f12_87.wmf"_[0v
per funzioni da integrare (funzioni integrande) limitate e generalmente continue in [a,b], cioè integrabili, valgono le seguenti proprietà:
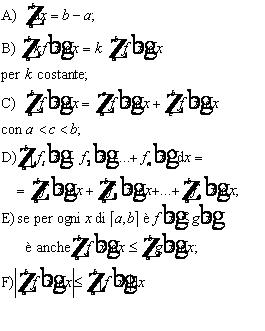 _[1v\h8"f12_88.wmf"_[0v
_[1v\h8"f12_88.wmf"_[0v
poiché anche | f(x) | ammette i. se lo ammette f(x); G) se f(x) e g(x) sono integrabili in [a,b] e g(x) non cambia mai segno in [a,b], si ha
![]() _[1v\h8"f12_89.wmf"_[0v dove m è un op portuno valore,
compreso tra gli estremi inferiore e superiore, di f(x) in [a,b];
l'ultima proprietà è nota come teorema generalizzato della media. Se si
considera l'i. definito esteso non a tutto [a,b], ma
all'intervallo [a,x], con x<b, questo i. dipende dal
valore x considerato ed è una funzione di
_[1v\h8"f12_89.wmf"_[0v dove m è un op portuno valore,
compreso tra gli estremi inferiore e superiore, di f(x) in [a,b];
l'ultima proprietà è nota come teorema generalizzato della media. Se si
considera l'i. definito esteso non a tutto [a,b], ma
all'intervallo [a,x], con x<b, questo i. dipende dal
valore x considerato ed è una funzione di ![]() _[1v\h8"f12_90.wmf"_[0v detta funzione i. di f(x);
all'espressione
_[1v\h8"f12_90.wmf"_[0v detta funzione i. di f(x);
all'espressione![]() _[1v\h8"f12_90a.wmf"_[0v, dove C è una costante det ta costante di
integrazione, si dà il nome di i. indefinito. La funzione i. è una
funzione continua in [a,b] e costituisce una primitiva di f(x);
la derivata della funzione F(x) è cioè uguale alla funzione f(x).
Se f(x) presenta punti di discontinuità, F(x) è una
primitiva generalizzata. Due primitive di una f(x) differiscono
tra loro solo per una costante additiva. Per quanto detto, l'insieme di tutte
le primitive di una funzione f(x) costituisce l'i. indefinito di f(x).
Nota una primitiva j(x) di f(x) si ha
_[1v\h8"f12_90a.wmf"_[0v, dove C è una costante det ta costante di
integrazione, si dà il nome di i. indefinito. La funzione i. è una
funzione continua in [a,b] e costituisce una primitiva di f(x);
la derivata della funzione F(x) è cioè uguale alla funzione f(x).
Se f(x) presenta punti di discontinuità, F(x) è una
primitiva generalizzata. Due primitive di una f(x) differiscono
tra loro solo per una costante additiva. Per quanto detto, l'insieme di tutte
le primitive di una funzione f(x) costituisce l'i. indefinito di f(x).
Nota una primitiva j(x) di f(x) si ha
![]() _[1v\h8"f12_91.wmf"_[0v
_[1v\h8"f12_91.wmf"_[0v
Questa formula viene detta formula fondamentale del
calcolo integrale. Spesso il numero j(b)-j(a) viene indicato con il simbolo ![]() _[1v\h8"f12_1002.wmf"_[0v. Consideriamo, p. es., la funzione
_[1v\h8"f12_1002.wmf"_[0v. Consideriamo, p. es., la funzione
![]() _[1v\h8"f12_1003.wmf"_[0v
_[1v\h8"f12_1003.wmf"_[0v
Essa è continua per ogni x>0; il suo grafico è
rappresentato in fig. 2. Vogliamo calcolare l'integrale definito da 1 a 2 di
tale funzione. La funzione ![]() _[1v\h8"f12_1004.wmf"_[0v è una primiti-va della funzione f(x).
Applicando la formula fondamentale del calcolo integrale, otteniamo:
_[1v\h8"f12_1004.wmf"_[0v è una primiti-va della funzione f(x).
Applicando la formula fondamentale del calcolo integrale, otteniamo:
![]() _[1v\h8"f12_92.wmf"_[0v
_[1v\h8"f12_92.wmf"_[0v
La porzione di piano, indicata con A nella fig. 2 delimitata
dal grafico della funzione, dall'asse delle x e dalle rette verticali di
equazioni x=1 e x=2 ha dunque area uguale a ![]() _[1v\h8"f12_1005.wmf"_[0v. Gli i. indefinitidelle funzioni più importanti,
detti i. indefiniti fondamentali, sono indicati nella tabella. Si usano,
nel calcolo degli i., alcune importanti formule, valide sia per gli i.
definiti, sia per gli i. indefiniti. La prima è un'immediata conseguenza della
regola di derivazione del prodotto di due funzioni ed è detta formula di
integrazione per parti:
_[1v\h8"f12_1005.wmf"_[0v. Gli i. indefinitidelle funzioni più importanti,
detti i. indefiniti fondamentali, sono indicati nella tabella. Si usano,
nel calcolo degli i., alcune importanti formule, valide sia per gli i.
definiti, sia per gli i. indefiniti. La prima è un'immediata conseguenza della
regola di derivazione del prodotto di due funzioni ed è detta formula di
integrazione per parti:
![]() _[1v\h8"f12_93.wmf"_[0v
_[1v\h8"f12_93.wmf"_[0v
dove f, f , g sono funzioni continue nell'intervallo di definizione, dotate di derivate prime, e G(x) è una primitiva di g(x); la funzione f(x) è detta fattore finito; mentre g(x)dx è detto fattore differenziale. P. es. sia da calcolare l'i. di cos x; si assuma cos x come fattore finito e cos x dx come fattore differenziale; si ha
 _[1v\h8"f12_94.wmf"_[0v
_[1v\h8"f12_94.wmf"_[0v
Un'altra formula, conseguenza immediata della regola di derivazione di funzione composta, è la formula di integrazione per sostituzione:
![]() _[1v\h8"f12_95.wmf"_[0v
_[1v\h8"f12_95.wmf"_[0v
dove g(z) è una funzione continua in un
intervallo [c,d], e f(x) è continua nell'intervallo
[a,b] in cui a e b (a<b) sono il valore
minimo e il valore massimo assunti da g(z) in [c,d].
P. es., per calcolare l'integrale di (ax+b)mdx si pone ax+b=z, da cui x=(z-b)/a
dx=dz/a; perciò: ![]() _[1v\h8"f12_96.wmf"_[0v
_[1v\h8"f12_96.wmf"_[0v
INTEGRALI IMPROPRI O GENERALIZZATI
Quando la funzione f(x) non è definita in un punto dell'intervallo [a,b], si possono considerare gli i. impropri, o generalizzati. Supponiamo, p. es., che la funzione f(x) sia definita nell'intervallo aperto a sinistra e chiuso a destra (a,b], dato dalle x tali che a<x b. Supponiamo poi che il limite di f(x) per x tendente ad a sia uguale a infinito e che in ogni intervallo [a ,b] con a<a la funzione f(x) sia integrabile. Se esiste il limite, per a tendente ad a, dell'integrale da a a b della funzione f(x), si assume tale limite come i. generalizzato da a a b della funzione f(x). Si pone cioè
![]() _[1v\h8"f12_97.wmf"_[0v
_[1v\h8"f12_97.wmf"_[0v
Calcoliamo, p. es., l'i. definito da 0 a 1 della funzione ![]() _[1v\h8"f12_1006.wmf"_[0v. Tale funzione non è definita in 0. Si ha:
_[1v\h8"f12_1006.wmf"_[0v. Tale funzione non è definita in 0. Si ha: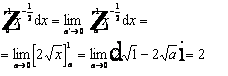 _[1v\h8"f12_98.wmf"_[0v
_[1v\h8"f12_98.wmf"_[0v
Notiamo che la curva di equazione ![]() _[1v\h8"f12_1007.wmf"_[0v ha come asintoto verticale l'asse delle y.
Dal calcolo dell'i. appena fatto segue che la porzione di piano, indicata con B
nella fig. 2, delimitata dal grafico della funzione, dall'asse delle x,
dall'asse delle y e dalla retta verticale di equazione x=1 ha
area uguale a 2. In tal modo si definisce l'i. generalizzato di una funzione
definita nell'intervallo chiuso a sinistra e aperto a destra [a,b)
dato dalle x tali che a x<b.
L'i. generalizzato, nel caso in cui la funzione f(x) sia definita
in un intervallo [a,b] escluso un punto c interno
all'intervallo [a,b] e la funzione f(x) sia
integrabile in ognuno degli intervalli [a,c-e], [c+e¢, b] con e>0, e¢>0 qualunque, lo si
definisce ponendo
_[1v\h8"f12_1007.wmf"_[0v ha come asintoto verticale l'asse delle y.
Dal calcolo dell'i. appena fatto segue che la porzione di piano, indicata con B
nella fig. 2, delimitata dal grafico della funzione, dall'asse delle x,
dall'asse delle y e dalla retta verticale di equazione x=1 ha
area uguale a 2. In tal modo si definisce l'i. generalizzato di una funzione
definita nell'intervallo chiuso a sinistra e aperto a destra [a,b)
dato dalle x tali che a x<b.
L'i. generalizzato, nel caso in cui la funzione f(x) sia definita
in un intervallo [a,b] escluso un punto c interno
all'intervallo [a,b] e la funzione f(x) sia
integrabile in ognuno degli intervalli [a,c-e], [c+e¢, b] con e>0, e¢>0 qualunque, lo si
definisce ponendo
![]() _[1v\h8"f12_99.wmf"_[0v
_[1v\h8"f12_99.wmf"_[0v
purché i due limiti del secondo membro esistano e siano
finiti. In tutti questi casi si hanno i seguenti criteri che permettono di
stabilire delle condizioni sufficienti per la convergenza dell'i. ![]() _[1v\h8"f12_100.wmf"_[0v (ci
si può limitare, senza che venga meno la generalità, al caso in cui il punto di
infinito sia situato all'estremo destro b dell'intervallo di
integrazione): se per x tendente a b la f(x) è
infinita di ordine minore o uguale ad a, con a<1, essa è integrabile; se per x tendente
a b la f(x) è infinita di ordine 1 e mantiene segno costante in
un intorno di b, essa non è integrabile. Analogamente si definisce l'i.
generalizzato esteso a un intervallo illimitato, ponendo:
_[1v\h8"f12_100.wmf"_[0v (ci
si può limitare, senza che venga meno la generalità, al caso in cui il punto di
infinito sia situato all'estremo destro b dell'intervallo di
integrazione): se per x tendente a b la f(x) è
infinita di ordine minore o uguale ad a, con a<1, essa è integrabile; se per x tendente
a b la f(x) è infinita di ordine 1 e mantiene segno costante in
un intorno di b, essa non è integrabile. Analogamente si definisce l'i.
generalizzato esteso a un intervallo illimitato, ponendo:
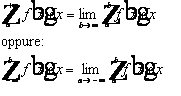 _[1v\h8"f12_101.wmf"_[0v
_[1v\h8"f12_101.wmf"_[0v
purché la f(x) ammetta i. in un intervallo
comunque esteso e i limiti esistano finiti. Calcoliamo, p. es., l'i. definito
da 2 a +
della funzione ![]() _[1v\h8"f12_1008.wmf"_[0v Si ha:
_[1v\h8"f12_1008.wmf"_[0v Si ha:
![]() _[1v\h8"f12_102.wmf"_[0v
_[1v\h8"f12_102.wmf"_[0v
Da ciò deriva che la funzione non è integrabile
nell'intervallo [2,+ ) dato dalle x tali che b x. La curva di equazione ![]() _[1v\h8"f12_1009.wmf"_[0v ha come asintoto orizzontale l'asse delle x.
Dal calcolo dell'i. appena fatto segue che la porzione di piano, indicata con C
nella fig. 2, delimitata dal grafico della funzione, dall'asse delle x e
dalla retta verticale di equazione x=2 ha area infinita. Anche nel caso
di i. definiti in intorni illimitati si può stabilire un criterio sufficiente
per l'integrabilità per il quale se f(x), in [a,+ ] o in [- ,b], è infinitesima di
ordine ³a,
con a>1,
essa ammette i.; se invece essa è infinitesima di ordine 1 e mantiene segno costante
per x>a (o per x<b) essa non è integrabile.
_[1v\h8"f12_1009.wmf"_[0v ha come asintoto orizzontale l'asse delle x.
Dal calcolo dell'i. appena fatto segue che la porzione di piano, indicata con C
nella fig. 2, delimitata dal grafico della funzione, dall'asse delle x e
dalla retta verticale di equazione x=2 ha area infinita. Anche nel caso
di i. definiti in intorni illimitati si può stabilire un criterio sufficiente
per l'integrabilità per il quale se f(x), in [a,+ ] o in [- ,b], è infinitesima di
ordine ³a,
con a>1,
essa ammette i.; se invece essa è infinitesima di ordine 1 e mantiene segno costante
per x>a (o per x<b) essa non è integrabile.
INTEGRALE DI LEBESGUE
Estensione della nozione di i. definito, alla quale si
pervie ne osservando che l'i. ![]() _[1v\h8"f12_103.wmf"_[0v, qualora f(x) sia integrabile, ma
non continua in [a,b], può considerarsi come limite di analoghi
i. le cui funzioni integrande siano continue. Precisamente, se f(x)
è una funzione quasi-continua, i suoi punti di discontinuità costituiscono un
insieme appartenente ad [a,b] avente misura complessiva minore di
un e
comunque piccolo; allora si può associare alla f(x) delle
funzioni ge(x) che
siano continue in tutto [a,b]. Se esiste finito il
_[1v\h8"f12_103.wmf"_[0v, qualora f(x) sia integrabile, ma
non continua in [a,b], può considerarsi come limite di analoghi
i. le cui funzioni integrande siano continue. Precisamente, se f(x)
è una funzione quasi-continua, i suoi punti di discontinuità costituiscono un
insieme appartenente ad [a,b] avente misura complessiva minore di
un e
comunque piccolo; allora si può associare alla f(x) delle
funzioni ge(x) che
siano continue in tutto [a,b]. Se esiste finito il![]() _[1v\h8"f12_104.wmf"_[0v si assume questo valore come l'i. di Lebesgue
della f(x) relativo ad [a,b]. Esso coincide con
l'i. di Riemann se la f(x) è continua in [a,b].
_[1v\h8"f12_104.wmf"_[0v si assume questo valore come l'i. di Lebesgue
della f(x) relativo ad [a,b]. Esso coincide con
l'i. di Riemann se la f(x) è continua in [a,b].
INTEGRALE CURVILINEO
I. curvilineo della funzione f(x,y), continua nel campo chiuso A, esteso alla curva C del piano (x,y) definita da x=x(t), y=y(t), con (a t b) e x(t), y(t) continue in [a,b] e tali che ogni punto [x(t), y(t)] appartenga ad A, relativo alla funzione u(t) (a t b), continua insieme con la propria derivata u (t), è il limite della somma
![]() _[1v\h8"f12_105.wmf"_[0v
_[1v\h8"f12_105.wmf"_[0v
dove a=t ,t ,...,tr,...,tn=b sono un numero finito di punti che dividono
l'intervallo [a,b] e hr è un valore qualsiasi dell'intervallo [tr ,tr], quando tende a zero la massima delle ampiezze in cui è
stato diviso l'intervallo (a,b). Viene in dicato con la notazione ![]() _[1v\h8"f12_106.wmf"_[0v Si può dimostrare che
_[1v\h8"f12_106.wmf"_[0v Si può dimostrare che
![]() _[1v\h8"f12_106a.wmf"_[0v
_[1v\h8"f12_106a.wmf"_[0v
Se u(t)=t e la curva C è rettificabile, allora l'i. curvilineo della f(x,y) diventa:
![]() _[1v\h8"f12_107.wmf"_[0v
_[1v\h8"f12_107.wmf"_[0v
in cui x=x(s), y=y(s) sono equazioni parametriche con 0 s L, essendo L la lunghezza della curva. Se f(x,y) 0, l'i. curvilineo rappresenta l'area della parte di superficie cilindrica con generatrici parallele all'asse z e avente come direttrice la curva C, che è compresa tra il piano (x,y) e la superficie z=f(x,y).
INTEGRALE DEFINITO PLURIDIMENSIONALE
La nozione di i. definito è suscettibile di un'importante
estensione cui si arriva quando si opera su funzioni di due o più variabili e
quindi il campo di integrazione è un dominio a due o più dimensioni. Ci si può
limitare al caso n=2, essendo immediata l'estensione al caso n
> 2. Si consideri una funzione f(x,y), definita in un
campo A limitato del piano xy. Si divida A in n
parti A ,A ,...,An in un qualunque modo e sia fr il valore di f(x,y) in un
qualsiasi punto di Ar e si consideri la somma ![]() _[1v\h8"f12_108.wmf"_[0v Se
al variare della suddivisione considerata e al tendere a zero delle aree delle
parti in cui è stato diviso A, esiste finito il lim
_[1v\h8"f12_108.wmf"_[0v Se
al variare della suddivisione considerata e al tendere a zero delle aree delle
parti in cui è stato diviso A, esiste finito il lim ![]() _[1v\h8"f12_109.wmf"_[0v, dove h è il massimo diametro di cerchi
contenenti le aree A ,...,An, allora la funzione f(x,y) è
integrabile nel campo A e l'i. si indica con la notazione
_[1v\h8"f12_109.wmf"_[0v, dove h è il massimo diametro di cerchi
contenenti le aree A ,...,An, allora la funzione f(x,y) è
integrabile nel campo A e l'i. si indica con la notazione 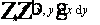 _[1v\h8"f12_110.wmf"_[0v Esso, nel caso in cui si abbia f(x,y) 0 per ogni (x,y)
appartenente ad A, rappresenta il volume del cilindroide costituito dai
punti (x,y,z) tali che (x,y) appartiene ad A
ed è 0 z f(x,y). Le
condizioni di integrabilità si ottengono, con semplici estensioni, da quelle
già stabilite per gli i. unidimensionali. Per il calcolo di un i.
bidimensionale, o i. doppio, si usa una delle due seguenti formule:
_[1v\h8"f12_110.wmf"_[0v Esso, nel caso in cui si abbia f(x,y) 0 per ogni (x,y)
appartenente ad A, rappresenta il volume del cilindroide costituito dai
punti (x,y,z) tali che (x,y) appartiene ad A
ed è 0 z f(x,y). Le
condizioni di integrabilità si ottengono, con semplici estensioni, da quelle
già stabilite per gli i. unidimensionali. Per il calcolo di un i.
bidimensionale, o i. doppio, si usa una delle due seguenti formule:
![]() _[1v\h8"f12_111.wmf"_[0v
_[1v\h8"f12_111.wmf"_[0v
in cui il campo A del piano (x,y) è definito dalle seguenti disuguaglianze:c y d, u(y) x v(y) con u(y) e v(y) funzioni continue in c y d e u(y) v(y); B)
![]() _[1v\h8"f12_112.wmf"_[0v
_[1v\h8"f12_112.wmf"_[0v
dove il campo A è definito dalle seguenti disuguaglianze:
![]() _[1v\h8"f12_113.wmf"_[0v
_[1v\h8"f12_113.wmf"_[0v
e h(x) e k(x) sono funzioni
continue in a x b e h(x) k(x). P. es., si debba calcolare ![]() _[1v\h8"f12_114.wmf"_[0v
_[1v\h8"f12_114.wmf"_[0v
dove A è il campo limitato dalla parabola y=1-x e dall'asse x. Utilizzando la B) si ha che I è uguale a:
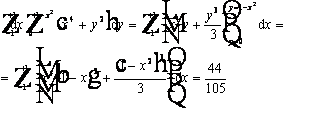 _[1v\h8"f12_115.wmf"_[0v
_[1v\h8"f12_115.wmf"_[0v
Allo stesso risultato si arriva usando la A):
![]() _[1v\h8"f12_116.wmf"_[0v
_[1v\h8"f12_116.wmf"_[0v
Anche
per gli i. doppi esistono le generalizzazioni relative a funzioni illimitate
oppure a i. estesi a campi illimitati. Di importanza notevole sono infine le
formule di Gauss-Green, che permettono di ricondurre un i. superficiale, cioè
doppio, a un i. curvilineo. La prima formula è:![]() _[1v\h8"f12_117.wmf"_[0v
_[1v\h8"f12_117.wmf"_[0v
dove A è un
campo definito come per la formula A) vista sopra, g è il suo contorno e B(x,
y) è una funzione continua in A insieme alla propria derivata
parziale![]() _[1v\h8"f12_118.wmf"_[0v
_[1v\h8"f12_118.wmf"_[0v
La seconda formula è:
![]() _[1v\h8"f12_118a.wmf"_[0v
_[1v\h8"f12_118a.wmf"_[0v
dove D e B sono funzioni continue in A insieme alle derivate parziali D/ y e B/ x. Nei secondi membri delle due formule compaiono gli i. curvilinei estesi al contorno g di A percorso in senso antiorario.
INTEGRALI DIFFERENZIALI ESATTI
Estesi a una curva tracciata nel campo in cui le funzioni formano un differenziale esatto, dipendono solo dagli estremi della curva e non dalla particolare curva scelta; se la curva è chiusa l'i. è nullo.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025