CATENE DI MARKOV A TEMPO DISCRETO

matematica

CATENE DI MARKOV A TEMPO DISCRETO

Nelle catene di Markov a tempo discreto gli istanti di transizione si verificano a istanti di tempo discreti.Ne è un esempio la linea transfer: è una macchina operatrice che compie sui pezzi una 949e46j sequenza di operazioni ed è trattabile come una catena di Markov perché la probabilità sul numero di pezzi al ciclo successivo dipende esclusivamente dal numero di pezzi presentati al ciclo attuale, e la preobabilità di avere un nuovo pezzo al termine di un ciclo è indipendente dagli eventi passati.

Applicando la definizione di processo di Markov alle catene a tempo discreto, si vede che le probabilità condizionate dipendono esclusivamente dai valori  e assunti dal processo a due istanti di tempo contigui:

dove  rappresenta la probabilità che in un periodo di campionamento, la variabile abbia una transizione dal valore al valore .L'insieme di tutte le probabilità di transizione viene organizzato nella matrice di transizione

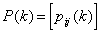
Vale l'equazione di Chapman Kolmogorov

Se però la catena di Markov è omogenea, ovvero se la matrice del periodo di transizione non dipende dal tempo, la soluzione è:

(PROLESSI STAZIONARIA)

detta equazione dinamica di un sistema a tempo discreto

e'  molto importante stabilire le condizioni di ergodicità della catena di Markov, cioè verificare in quali condizioni le probabilità di stato raggiungono un valore stazionario al crescere del tempo, indipendente dalle condizioni iniziali.

Il vettore delle probabilità di stato a regime soddisfa la condizione:

Mentre la probabilità a regime è data dalla soluzione:

La convergenza del sistema di equazioni impone che gli autovalori della matrice P siano

ma poiché uno degli autovalori è uguale a 1, viene richiesto che l'autovalore sia unico.

Da un punto di vista algebrico le probabilità di stato a regime vengono calcolate mediante il metodo di bilanciamento dei flussi.