DIMOSTRARE LE PROPRIETA' DEL VALORE ATTESO DELLE VARIABILI CASUALI

matematica

DIMOSTRARE LE PROPRIETA' DEL VALORE ATTESO DELLE VARIABILI

CASUALI.

Definizione VARIABILE CASUALE:

La variabile casuale è una funzione che assegna un valore a ciascun evento semplice.

Variabili Casuali Indipendenti:

Due variabili si dicono indipendenti se presa una coppia qualsiasi dei val 939b12j ori (x,y) la probabilità  N.B.: il concetto è simile all'intersezione di una probabilità.

Valore Atteso:

Siano:

 i risultati di un esperimento.

 le frequenze relative associate alle r.

 le variabili casuali associate.

La media aritmetica ponderata dei valori di Z è:

 

che, con l'aumentare delle frequenze relative, diventa l'Aspettativa:

Proprietà:

1) E(c) = c;

2) E(c+Z)= cE(Z);

3) E(CZ)= cE(Z) ;

4)E(X+Y)= E(X)+E(Y) ;

5)E(XY)=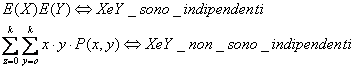

Dimostrazioni:

1) E(c) = c;

Si sa che P(Z=c)=1 E(c)=cP(Z=c)=1.

2) E(c+Z)= cE(Z);

Sia Y=c+Z

Da cui si nota che:

.

3) E(CZ)= cE(Z) ;

Sia Y= cZ

Da cui

4)E(X+Y)= E(X)+E(Y) ;

Sia Z=X+Y

Allora

.

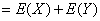5)E(XY)=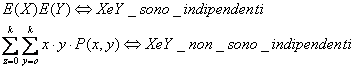

non si dimostra.