|
|
| |
ALCUNI ESERCIZI DA TEMI DI ESAME DI FONDAMENTI DI RICERCA OPERATIVA B
Avvertenza: essendo presi da compiti di precedenti anni non sempre la suddivisione fra esercizi sulla prima e la seconda parte del corso è rispettata.
B&B + PL
Esercizio 2 - Si consideri il seguente problema di programmazione lineare intera (PLI):
Max
2.a) Risolvere il rilassamento continuo del problema per via grafica.
2.b) Applicare un metodo di Branch-and-Bound per risolvere il problema di PLI assegnato, continuando a
calcolare il bound di ogni nodo dell' albero decisionale per via grafica. Si faccia branch dapprima
sulla variabile x1.
2.c) Risolvere il duale del problema rilassato del punto 2.a col metodo degli scarti complementari.
2.d) Determinare la matrice di base corrispondente alla soluzione ottima del duale e verificarne l'ottimalità calcolando i costi ridotti delle variabili non in base.
2.e) Dimostrare il teorema degli scarti complementari.
B&B + Lagrangiana
Esercizio 3 - Si consideri il seguente problema di Zaino Binario:
Max 5 }
3.a) Risolvere il problema con un metodo di Branch-and-Bound utilizzando il bound di Dantzig.
3.b) Scrivere il rilassamento Lagrangiano del problema.
3.c) Dimostrare che tale rilassamento gode della proprietà di integralità e dirne le conseguenze.
PNL vincolata (KKT)
Esercizio 4 - Nonostante la crisi la pregiata casa vinicola Bacchino può contare su un notevole portafoglio di ordini. Vuole quindi acquistare da una ditta specializzata un elevato numero di contenitori di carta plastificata tecnologicamente all' avanguardia. Per ovvie ragioni di facilità di imballaggio, i contenitori devono avere la forma di un parallelepipedo a base quadrata. Il costo di ciascun contenitore è formato da una parte g proporzionale alla superficie totale del parallelepipedo più una parte fissa f data dal costo del tappo di chiusura. Detto x il lato della base per ragioni estetiche si desidera che l' altezza y sia almeno 2x. Il volume minimo di ciascun contenitore deve essere uguale a q.
4.a) Formulare il problema di minimizzare il costo dei contenitori rispettando i vincoli con un modello di
Programmazione Non-lineare.
4.b) Scrivere
4.c) Scrivere tutte le condizioni di KKT.
4.d) Trovare la soluzione ottima in funzione di q applicando le condizioni di KKT.
4.e) Porre q = 1000 cm3 (un litro) e calcolare le dimensioni ottime in cm di ogni contenitore.
Gomory
Esercizio 3 - Si consideri il seguente problema di PLI:
max .
3.a) Disegnare la regione di ammissibilità del problema.
3.b) Risolvere il rilassamento continuo del problema per via grafica.
3.c) Scrivere il problema in forma standard introducendo le variabili ausiliarie x3, x4. e x5.
3.d) Calcolare l'inversa della matrice di base B corrispondente all' ottimo trovato al punto (b).
3.e) Moltiplicare a sinistra per tale inversa il sistema dei vincoli ottenuto in (c) e calcolare i tagli di Gomory
in forma intera derivabili da tale sistema di vincoli.
x1 e x2.
3.g) Dimostrare graficamente che è sufficiente considerare uno solo di questi tagli per 919h73j ché gli altri sono
dominati da esso.
3.h) Risolvere graficamente il rilassamento continuo del problema ottenuto. Si ottiene così la soluzione
ottima dell' originale problema di PLI: perché ?
PNL vincolata (KKT)
Esercizio 4 Si consideri il seguente problema di Ottimizzazione Non-Lineare:
min
4.a) Dire se il problema è convesso oppure no, giustificando la risposta.
4.b) Scrivere
4.c) Scrivere tutte le condizioni di KKT.
4.d) Risolvere il problema utilizzando le condizioni di KKT.
4.e) Si può affermare che il problema è di Programmazione Quadratica ? (giustificare)
4.g) Il punto ottenuto in (
B&B + Lagrangiana + complessità
Esercizio 3 - Una società di venture capital dispone di 40 milioni di euro e deve decidere quali finanziare tra 7 diversi progetti caratterizzati dai costi di start-up e dai profitti attesi riportati in nella tabella seguente (pure in milioni di euro):
progetto 1 2 3 4 5 6 7
costo 8 20 10 8 12 10 20
profitto 4 8 3 2 3 2 3
3.a) Formulare il problema di massimizzare il profitto atteso come problema di Zaino Binario.
3.b) Mediante un metodo di branch-and-bound guidato dal bound di Dantzig, determinare la scelta ottima. (Suggerimento: ramificare (branch) partendo sempre dal nodo con variabile posta a 0 dell' albero decisionale).
3.c) Scrivere il problema ottenuto dal rilassamento Lagrangiano del vincolo di budget. Cosa significa affermare che tale rilassamento gode della proprietà di integralità ?
3.d) Scrivere la forma di riconoscimento di un generico problema di Zaino Binario e spiegare cosa significa dire che tale problema non è Fortemente NP-completo.
3.e) Calcolare quanti bit sono necessari per codificare i dati di ingresso di un generico problema di Zaino Binario, caratterizzato da capacità C, da n progetti, e da profitto massimo P.
Ottimizzazione non-lineare senza vincoli
Esercizio 4 - Si consideri il seguente problema di programmazione non-lineare senza vincoli:
min .
4.a) Scrivere il gradiente g e l' Hessiano G della funzione f.
4.b) Calcolare il valore di f, g e G nel punto (0,2).
4.c) Dimostrare che G è definito positivo in tale punto.
4.d) Applicare un passo del metodo di Newton a partire dal punto (0,2) e verificare che il valore di f diminuisce.
4.e) Il metodo di Newton non è globalmente convergente: cosa significa questa affermazione ?
Problemi polinomiali su grafi
Esercizio 1 - Si deve progettare una rete di acquedotti che consenta ad un serbatoio montano di rifornire cinque città. I tratti di acquedotto che è possibile costruire sono riportati nella tabella seguente con i rispettivi costi (in milioni di euro).
DA A costo
__________ ______ ____ __________ ______ ____ __
terminale città 1 2
terminale città 2 7
terminale città 5 8
città 1 città 2 4
città 1 città 5 7
città 2 città 3 8
città 2 città 5 6
città 2 città 4 9
città 3 città 4 7
città 4 città 5 5
città 5 città 3 3
1.a) Disegnare il digrafo corrispondente riportando tutti i costi sugli
archi e assegnando nodi numerati da
1.b) Determinare l'arborescenza (cioè l'albero orientato) di costo totale minimo dal terminale (nodo 6) a tutti gli altri nodi.
1.c) Determinare col metodo di Dijkstra l'albero dei cammini minimi dal
nodo
1.d) Analizzare l'algoritmo impiegato al punto 1.b (detto talvolta algoritmo di Edmonds) e dimostrare che la sua complessità è O(n2).
PL
Esercizio 2 - Si consideri il seguente problema di PL:
Max
2.a) Risolvere il problema per via grafica.
2.b) Scrivere il duale del problema dato.
2.c) Risolvere il duale col metodo degli scarti complementari.
2.d) Determinare la matrice di base corrispondente alla soluzione ottima del duale e verificarne l'ottimalità calcolando i costi ridotti delle variabili non in base.
2.e) Dimostrare il teorema degli scarti complementari.
Zaino (B&B + integralità)
Esercizio 3 - Si consideri il seguente problema di Zaino Binario:
max " i }.
3.a) Risolvere il problema con un metodo di Branch-and-Bound utilizzando il bound di Dantzig.
3.b) Scrivere il rilassamento Lagrangiano del problema.
3.c) Dimostrare che tale rilassamento gode della proprietà di integralità e dirne le conseguenze.
KKT
Esercizio 4 Si vuole massimizzare il prodotto xy con i seguenti vincoli: x 0, y 4, x + y 6, 2x - y 6.
4.a) Scrivere
4.b) Scrivere tutte le condizioni di KKT.
4.c) Dimostrare che i punti (3,3) e (2,4) soddisfano alle KKT e trovare i valori dei moltiplicatori corrispondenti.
4.d) Dimostrare che gli unici altri punti che soddisfano alle condizioni di KKT sono quelli del segmento di asse delle ordinate compresi fra y = - 6 e y = 0.
4.e) Quale fra tutti i punti che soddisfano alle KKT fornisce il valore ottimo ?
Problemi polinomiali su grafi
Esercizio 1 Un gestore di reti di telecomunicazione possiede la rete in figura. La rete collega tra loro alcuni edifici che sono sedi di molte compagnie. Le lunghezze delle tratte che compongono la rete sono riportate in figura. Tre dei suoi clienti gli pongono tre diversi problemi, riportati ai punti a, b e c. Per ciascuno di essi individuare il problema su grafo a cui fanno riferimento e dare la soluzione ottima illustrando i vari passi degli algoritmi usati.
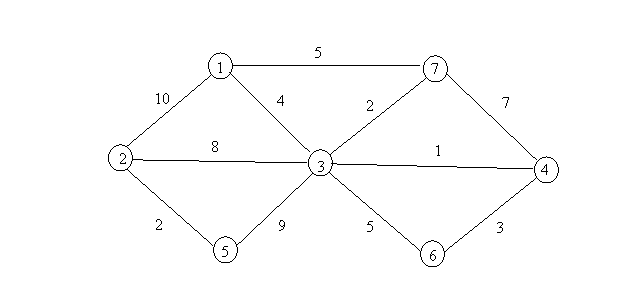
1.a) Il primo cliente richiede una sottorete che garantisca la connessione tra tutti i nodi. E' necessario quindi riservare alcuni canali trasmissivi al cliente. I canali trasmissivi che si possono affittare offrono capacità in entrambi i sensi sufficiente a instradare tutto il traffico del cliente. E' dunque necessario affittare un solo canale trasmissivo su ciascuna delle tratte scelte per garantire la connessione. Il costo di un canale trasmissivo è proporzionale alla lunghezza della tratta su cui è installato. Il cliente vuole minimizzare il costo della rete affittata.
1.b) Il secondo cliente ha già affittato i canali su tutte le tratte, ma deve determinare il percorso dei pacchetti dalla sorgente (nodo 1) a tutte le destinazioni. Per il tipo di protocollo usato, l'instradamento deve avvenire sul percorso più breve.
1.c) Anche il terzo cliente ha già affittato banda
su tutte le tratte. Si è reso conto di avere ancora capacità disponibile sulle
tratte, ma solo in una direzione. Le direzioni in cui c'è capacità disponibile
sono indicate in tabella. Il cliente vorrebbe sfruttare la capacità disponibile
per trasmissioni broadcast dalla sorgente
|
Tratta |
Direzione con capacità disponibile |
|
1,2 |
1 2 |
|
1,3 |
1 3 |
|
1,7 |
1 7 |
|
2,3 |
2 3 |
|
2,5 |
2 5 |
|
3,4 |
4 3 |
|
3,5 |
3 5 |
|
3,6 |
3 6 |
|
3,7 |
7 3 |
|
4,6 |
6 4 |
|
4,7 |
7 4 |
PL
Esercizio 2 - Si consideri il seguente problema di Programmazione Lineare (PL):
max
4.a) Scrivere il duale del problema dato.
4.b) Scrivere le equazioni delle condizioni di complementarietà degli scarti complementari.
4.c) Ricavare le soluzioni duali complementari per i punti (4,4) e (2,6).
4.d) Dire quali dei due punti sono soluzione ottima del problema e giustificare la risposta.
4.e) Mostrare, per gli eventuali punti di ottimo, che la soluzione ottima primale e duale coincidono.
Zaino Binario con B&B e Lagrangiani
max
3.a) Risolvere il problema applicando il metodo del branch and bound, calcolando, ad ogni nodo, il rilassamento continuo applicando il bound di Dantzig. Applicare la strategia depth first di visita dell'albero di ricerca e visitare per primi i nodi in cui la variabile di branch è posta a 0.
3.b) Scrivere il rilassamento lagrangiano del problema, usando un moltiplicatore u 0.
3.c) Calcolare il valore del rilassamento lagrangiano per u = 4.
3.d) Tale valore corrisponde ad una soluzione ammissibile anche per il problema originale. Come mai non è
quella ottima ?
PL
Esercizio 1 - Si consideri il seguente problema di PL:
Max
1.a) Scrivere il problema in forma standard.
1.b) Calcolare la matrice inversa relativa alla base x1,x2.
1.c) Verificare che la base x1,x2 sia ammissibile.
1.d) Scrivere il problema duale.
1.e) Verificare che la base è ottima applicando le condizioni di complementarietà.
Problemi polinomiali su grafi
Esercizio 2 - Un impianto industriale è composto da diversi edifici:
Alcuni di questi edifici sono collegati da strade asfaltate, che possono essere percorse in entrambi i sensi, secondo quanto riportato in tabella:
DA A lunghezza
__________ ______ ____ __________ ______ ____ __________
ingresso officina A 3
ingresso officina B 11
ingresso mensa 6
ingresso uffici 5
officina B officina A 2
officina B mensa 6
officina B lab. ricerca 8
mensa lab. ricerca 7
mensa lab. prototipazione 4
mensa uffici 3
lab. prototipazione lab. ricerca 8
lab. prototipazione uffici 3
2.a) Disegnare il grafo G dove ad ogni nodo corrisponde un edificio e ogni lato rappresenta la connessione fra due edifici. Per ognuna delle domande seguenti individuare il problema di ottimizzazione da risolvere su G.
2.b) La direzione dell'impianto ha deciso di far costruire dei passaggi coperti lungo alcune delle strade, per garantire, in caso di pioggia, di poter andare da un edificio all'altro senza bagnarsi. La costruzione di un percorso coperto ha un costo proporzionale alla lunghezza del percorso stesso: individuare le strade su cui costruire i passaggi coperti in modo da minimizzare il costo.
2.c) L'unica uscita è situata nell'edificio dell'ingresso: in caso di emergenza tutti i lavoratori devono evacuare l'area raggiungendo l'ingresso. Trovare il percorso da seguire a partire da ogni edificio per garantire che l'area sia evacuata il più rapidamente possibile, sapendo che il tempo di percorrenza di una strada è proporzionale alla sua lunghezza.
2.d) Per garantire la sicurezza. lo stato dell'asfalto deve essere controllato di frequente. Trovare il percorso più veloce che garantisca di controllare tutte le strade del complesso.
Gomory + B&B
Esercizio 3 - Si consideri il problema
Max
3.a) Risolvere per via grafica il problema in cui il vincolo di interezza è stato rilassato.
3.b) Trovare la base corrispondente alla soluzione ottima trovata.
3.c) Trovare la soluzione intera applicando il metodo del branch-and-bound, risolvendo ad ogni nodo il rilassamento continuo per via grafica.
3.d) Considerare il problema che si ottiene eliminando il secondo vincolo. Verificare che il punto di ottimo trovato in 3.b è ottimo anche per il nuovo problema rilassato.
3.e) Ricavare i tagli di Gomory relativi al nuovo problema e alla sua soluzione ottima.
3.g) Trovare la nuova soluzione ottima.
3.h) Il valore ottimo in presenza del taglio è maggiore o minore (considerando il problema di massimo) di quello precedente? Perché?
Problemi polinomiali su grafi
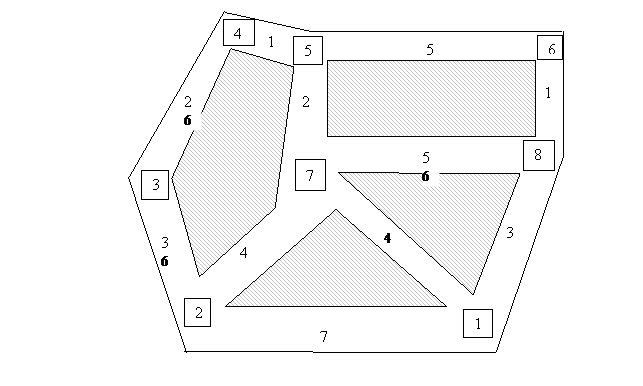
Esercizio 1 - A causa di ripetuti furti, un insieme di negozi, riuniti in una zona pedonale di una cittadina, ha deciso di ricorrere ad una compagnia di vigilanza privata. La zona pedonale è rappresentata in figura, insieme alla lunghezza delle strade lungo le quali si affacciano i vari negozi. La sede della vigilanza è in corrispondenza dell'incrocio 1. La sorveglianza ha due richieste, descritte ai punti b,c. Per ogni richiesta dire quale problema di ottimizzazione vi corrisponde, individuare il metodo di soluzione e trovare la soluzione ottima.
(1.a) Disegnare il grafo corrispondente alla zona pedonale (i nodi devono rappresentare gli incroci, i lati le strade).
(1.b) Il personale della ditta di vigilanza deve effettuare giri di controllo, durante i quali ogni strada deve essere percorsa almeno una volta. Si vuole determinare quale sia il percorso più breve che consente di controllare tutte le strade.
(1.c) Il personale, quando non è impegnato nei giri di controllo, sorveglia l'area dalla sede della vigilanza, grazie a un impianto di telecamere a circuito chiuso. Le telecamere sono posizionate in ogni incrocio ed è necessario installare i cavi che le collegano alla sede. I cavi devono essere installati lungo le strade ed il loro costo è proporzionale alla loro lunghezza. Si deve determinare su quali strade installare i cavi in modo da collegare tutte le telecamere alla sede a costo minimo.
PL
Esercizio 2 - Si consideri il seguente problema di programmazione lineare:
max
(2.a) Si scriva il problema duale. (Attenti ai segni e al verso delle disuguaglianze !)
(2.b) Si scrivano le equazioni degli scarti complementari (sia per il primale che per il duale).
(2.c) Date le soluzioni [x1=2, x2= -1] e [x1=3/2, x2=5/2] si trovi, per ciascuna, la soluzione duale complementare.
(2.d) Individuare geometricamente una soluzione ottima (Giustificare la risposta.)
(2.e) Quante sono le soluzioni ottime di base? E non di base? (Giustificare la risposta.)
Complessità
Esercizio 3 - (3.a) Che differenza c' è fra un problema di ottimizzazione e il suo corrispondente problema di riconoscimento ? (3.b) Definire le classi di problemi P ed NP. (3.c) Cosa significa dire che un problema è NP-completo ? (3.d) Cosa significa dire che un problema è NP-difficile ?
B&B
Esercizio 4 - Si consideri il seguente albero parziale di Branch-and-Bound per un problema di minimo, in
cui, per ogni nodo Pi, sono indicati il valore del rilassamento (LBi) e il valore della miglior soluzione trovata
euristicamente (UBi).
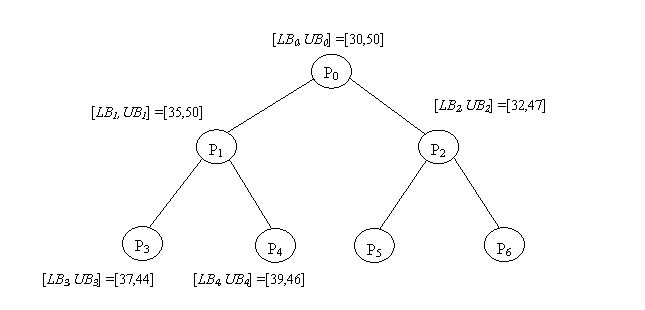
(4.a) Tra quali valori è compreso l'ottimo del problema ?
(4.b) Un successivo calcolo fornisce per il problema P5 una soluzione euristica di valore 37, mentre il valore di rilassamento resta uguale a 32. Quali nodi dell' albero decisionale restano attivi ?
Gomory
Esercizio 5 - Si consideri il seguente problema di Ottimizzazione Lineare Intera:
max .
Una volta introdotte le variabili ausiliarie, nel punto di ottimo del rilassamento continuo del problema le equazioni di vincolo sono:
x1 - 0,5 x 3 + 0,25 x5 = 2,75
x2 + 1,5 x3 - 0,25 x5 = 2,25
2 x3 + x4 + 0,5 x5 = 0,5
(5.a) Dire quali sono e quanto valgono le variabili di base e calcolare il valore ottimo di z.
(5.b) Scrivere i tagli di Gomory derivanti dalle equazioni di vincolo in forma intera e frazionaria.
(5.c) Fra questi tagli il più efficace è quello derivante dalla variabile x1 . Esprimere la forma intera di tale taglio in funzione delle sole variabili x1 , x2
(5.d) Disegnare sul piano la regione di ammissibilità del problema originale e riportarvi il taglio ottenuto al punto precedente.
(5.e) Spiegare geometricamente come mai esistono infinite soluzioni ottime fra le quali una intera, ma il metodo del Simplesso non sarebbe in grado di identificarla.
KKT
min
(6.a) Scrivere
(6.b) Risolvere il problema applicando le condizioni di Karush-Kuhn-Tucker.
(6.c) Si tratta di un problema di Programmazione Quadratica: cosa vuol dire questa affermazione ?
(6.d) Se invece del minimo volessimo il massimo sarebbe ancora vera l' affermazione precedente ?
B&B
Esercizio 4 - Risolvere il seguente problema di zaino binario col metodo di Branch-and-Bound utilizzando il bound di Dantzig (cioè il valore del rilassamento continuo arrotondato al massimo intero contenuto in tale valore). Ad ogni nodo dell' albero di decisione spiegare come viene calcolato il bound ed eventuali scelte di fissaggio delle variabili. Spiegare anche quando e come mai alcuni nodi vengono chiusi. Si consiglia fortemente di fare branch sempre sulla variabile frazionaria corrente.
Max , i=1,.,6
Complessità
Esercizio 5 - Si consideri il problema di ottimizzazione P, dove tutti i dati numerici sono interi:
min , i=1,.,n }.
5.a Scrivere la forma di riconoscimento P(k) di P introducendo come soglia il numero intero k.
5.b Dimostrare che P(k) appartiene alla classe NP.
5.c Cosa vuol dire affermare che P(k) è NP-completo ?
PNL senza vincoli
Esercizio 6 Si consideri il seguente problema di programmazione non-lineare senza vincoli:
min .
6.a Scrivere il gradiente g e l' Hessiano G della funzione f.
6.b Calcolare il valore di f, g e G nel punto (0,2).
6.c Dimostrare che G è definito positivo in tale punto.
6.d Applicare un passo del metodo di Newton a partire dal punto (0,2) e verificare che il valore di f diminuisce.
6.e Il metodo di Newton non è globalmente convergente: cosa significa questa affermazione ?
KKT
Esercizio
4 -
4.a) Formulare il problema di minimizzare il costo dei contenitori rispettando i vincoli con un modello di PNL.
4.b) Scrivere
4.c) Scrivere tutte le condizioni di KKT.
4.d) Trovare la soluzione ottima in funzione di k applicando le condizioni di KKT.
4.e) Porre V = 2000 cm3 (due litri) e calcolare le dimensioni ottime in cm di ogni contenitore.
PL
Esercizio 2 - Si consideri il seguente problema di Programmazione Lineare:
min
2.a Scrivere il problema duale (N.B. x4 non è vincolata in segno !)
2.b Eliminare eventuali ridondanze riducendo opportunamente le dimensioni del problema duale.
2.c Risolvere il problema duale per via geometrica.
2.d Determinare i valori ottimi delle variabili primali col metodo degli scarti complementari.
2.e Dimostrare il teorema della dualità debole della PL.
B&B + Gomory
Esercizio 3 Si consideri il seguente problema di Programmazione Lineare Intera (PLI):
max
3.a Disegnare la regione di ammissibilità mettendo in evidenza i punti a coordinate intere in essa contenuti.
3.b Risolvere geometricamente il rilassamento lineare del problema e dedurne una stima per eccesso del valore z* della soluzione ottima.
3.c Risolvere il problema di PLI col metodo di Branch-and-Bound facendo "branch" per prima sulla variabile frazionaria x1 .
3.d Ricavare il tableau ottimo corrispondente alla soluzione trovata al punto 3.b e scrivere i tagli di Gomory che risultano dal fatto che i valori delle variabili in base sono entrambi frazionari, sia in forma intera che frazionaria.
3.e Ricavare le disuguaglianze corrispondenti a tali tagli in funzione delle sole variabili x1 , x2 e riportarli sulla regione di ammissibilità disegnata al punto 3.a.
PNL (KKT)
Esercizio 4 - Un investitore J deve decidere come distribuire un budget B = 600 kEuro fra due fondi di investimento 1 e 2. Si indichino con x1 , x2 rispettivamente il numero di quote acquistate. Per il fondo 1 si sa che il prezzo di ogni quota è di 20 kEuro, il ritorno atteso per quota è di 5 kEuro, la varianza di 4 kEuro. Per il fondo 2 il prezzo per quota è di 30 kEuro, il ritorno atteso di 10 kEuro e la varianza di 100 kEuro. Gli altri coefficienti della matrice di covarianza sono entrambi di 5 kEuro. Si ha quindi che il ritorno totale atteso sarà
R = 5x1 + 10x2
mentre il rischio verrà valutato dalla funzione
V = 4x12 + 5x1x2 + 5x1x2 + 100x22.
4.a Formulare il problema di J come problema non-lineare di massimizzare la funzione R kV col vincolo di budget, dove k è un parametro compreso fra 0 e 1 che pesa l'importanza per J del rischio dell'investimento.
4.b Ponendo k uguale a 0 (caso di J interamente favorevole a rischiare), risolvere il problema di PL risultante trovando una stima superiore s al ritorno totale ottenibile. (Nota: non è necessario applicare il Simplesso data la banalità del problema).
4.c Porre k uguale a 0,1 e scrivere
4.d Scrivere tutte le condizioni di KKT per tale problema.
4.e Risolvere il problema trovando tutte le coppie di valori delle variabili che soddisfano alle condizioni di KKT e fra queste quella che fornisce la soluzione ottima. Quanto inferiore è il ritorno atteso ottenuto in queste condizioni rispetto alla stima superiore s calcolata in 4.b ?
Problemi di flusso
Esercizio 1 Una società estrae marmo da due cave C1 e C2 da cui ricava al massimo, rispettivamente, 400 e 200 t/giorno. Il marmo deve essere trasportato presso tre ditte X, Y e Z che rivendono non più di 100, 200 e 250 t/giorno, rispettivamente. Il costo del trasporto è proporzionale alla distanza fra cava e ditta e le distanze da ognuna delle cave ad ogni ditta sono riportate nella tabella seguente:
X Y Z
C1 30 20 25
C2 45 50 15
1.a) Formulare il problema di minimizzare il costo di trasporto totale come problema di flusso massimo a costo minimo, disegnando un'opportuna rete di flusso e assegnando opportunamente ai suoi archi capacità e costi unitari di flusso.
1.b) Attualmente la società trasporta dalla prima cava 200 t/giorno alla ditta Y e 150 t/giorno alla ditta Z, mentre dalla seconda cava trasporta 100 t/giorno alla ditta X e 50 t/giorno alla ditta Z. Mostrare che tale distribuzione non è di minimo costo.
1.c) Mostrare anche che la quantità di marmo distribuita come nel punto precedente può essere incrementata.
1.d) La distribuzione ottima (cioè quella che al minimo costo di trasporto soddisfa in pieno alle richieste delle tre ditte) si ottiene inviando tutta la quantità di marmo prodotta dalla seconda cava alla ditta Z. Determinare, usando se necessario il metodo di Ford-Fulkerson, come distribuire la quantità di marmo rimanente (350 t/giorno) a partire dalla prima cava a costo minimo.
KKT + convessità
Esercizio 4 Si consideri il seguente problema di Ottimizzazione Non-Lineare:
max
4.a) Dire se il problema è convesso oppure no, giustificando la risposta.
4.b) Scrivere
4.c) Scrivere tutte le condizioni di KKT.
4.d) Dimostrare sfruttando tali condizioni che sia x che y non possono essere uguali a zero.
4.e) Utilizzare il risultato del punto precedente per ottenere una Lagrangiana semplificata e determinare tutti i punti del piano x-y che soddisfano alle condizioni di KKT e fra questi quello ottimo.
Convessità e PNL
Esercizio 4 - Viene assegnato un poliedro limitato (un politopo) in n dimensioni
P =
3.a) Sapendo che P non contiene l'origine degli assi, formulare il problema di trovare il punto di P più vicino all'origine come problema di Programmazione Matematica Non-lineare. (adottare la metrica Euclidea.)
3.b) Dire se si tratta o no di un problema convesso, giustificando la risposta.
3.c) Quale metodo di ottimizzazione si adatterebbe meglio a risolverlo e perché ?
3.d) Se il problema fosse quello di trovare il punto di P massimamente distante dall'origine il problema sarebbe ancora convesso ? (Giustificare la risposta.)
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026