|
|
| |
Equivalenza asintotica e "o piccolo"
Siano f e g due funzioni definite in un
intorno di c (finito o infinito), e
sia g(x)
![]() .
.
La specificazione "per x c" può essere sottintesa ove non dia luogo ad equivoci.
La relazione di equivalenza asintotica è una relazione di equivalenza; ciò significa che soddisfa le proprietà:
riflessiva: f ~ f
simmetrica: f ~ g g ~ f
transitiva: f ~ g e g ~ h f ~ h.
Scelta una funzione g(x) come infinito (o infinitesimo) campione, per x c, se risulta f ~ k ga, con k costante 0, si dice che f è infinito (o infinitesimo) di ordine a rispetto a g, e che kga ne costituisce la parte principale. Usualmente si sceglie g(x) = x o g(x) = 1/x, a seconda dei casi.
Esempi:
a) per x
cos x ~ ex ~ Ch x ~ 1
sin x ~ tg x ~ ex - 1 ~ Sh x ~ Th x ~ log(1+x) ~ x
(1 + x)1/2 -1 ~ x/2 (e, in generale, (1 + x)a a x)
1 - cos x ~ Ch x - 1 ~ x2/2
p(x) = a xn + b xn-1 + . + k xm ~ k xm , monomio di grado minimo in p(x)(n > m 0; a, k
x - sin x ~ x3/6
(dunque rispetto all'infinitesimo g(x) = x, per x 0, sin x è un infinitesimo del primo ordine con parte principale x; 1 - cos x è un infinitesimo del secondo ordine con parte principale x2/2; 5x4 - 3x2 è un infinitesimo del secondo ordine con parte principale - 3x2; x - sin x è un in 313e49d finitesimo del terzo ordine con parte principale x3/6, ecc.)
b) per x
p(x) = a xn + b xn-1 + . + k xm ~ a xn , monomio di grado massimo in p(x)
Ch x ~ Sh x ~ ex /2
arctg x ~ p
p/2 - arctg x = arccotg x ~ 1/x
Th x ~ 1
(dunque rispetto all'infinito g(x) = x, per x , 5x4 - 3x2 è un infinito del quarto ordine con parte principale 5x4; p/2 - arctg x è un infinitesimo del primo ordine con parte principale 1/x, ecc.)
c) per x
log x ~ (x-1)
sin (px) ~ (1-x)
Si noti che, nei precedenti esempi a)b)c), in ciascuna riga l'ultima espressione è assai più semplice delle altre. Ciò facilita molto il calcolo di limiti e, più in generale, lo studio del comportamento di una funzione nell'intorno di x = c, se si sfruttano opportunamente le seguenti proprietà (si intende che tutti i limiti sono per x c):
f ~ g ed lim f(x) (o lim g(x)) lim f(x) = lim g(x)
(in particolare f ~ k R lim f(x) = k). Si badi che f ~ 0 non ha significato!
Il reciproco non vale, in generale, se i limiti sono 0 oppure
Controesempio: f(x) = x , g(x) = x2 per x 0 o per x hanno lo stesso limite (risp. 0 o ) ma non sono asintoticamente equivalenti.
f1 ~ g1 , f2 ~ g2 f1 f2 ~ g1 g2
(In un prodotto si può sostituire ciascun fattore con un altro asintoticamente equivalente)
Esempi:
per x log(1+x) ~ x , 1 - cos x ~ x2 /2 log(1+x) · (1 - cos x) ~ x3 /2
per x
f ~ g f a ~ g a (a R ( per a
(si può elevare a potenza entrambi i membri di una relazione di equivalenza asintotica)
Esempi:
per x sin x ~ x sin3 x ~ x3 , (sin x) ~ x
per x x3
+ 4x2 ~ 4x2 ![]() ~ (4x2) = 2 |x|
~ (4x2) = 2 |x|
per x x3 + 4x2 ~ x3
![]() ~ (x3) = x3/2
~ (x3) = x3/2
per x -4+ x3
+ 4x2 ~ 16(x+4) ![]() ~
~ ![]()
f1 ~ g1 , f2 ~ g2 f1 / f2 ~ g1 / g2
(In un quoziente si può sostituire ciascun termine con un altro asintoticamente equivalente)
Esempi:
a) per x
sin x ~ x , 1 - cos x ~ x2 /2, (1 - cos x)/ sin x ~ x/2
p(x) = a xn + b xn-1 + . + k xm ~ k xm ; P(x) = A xr + B xr-1 + . + K xs ~ K xs (k, K
p(x)/P(x) ~ (k/K) xm-s,
e quindi p(x)/P(x) 0 se m>s, k/K se m=s, se m<s
b) per x
p(x) = a xn + b xn-1 + . + k xm ~ k xm ; P(x) = A xr + B xr-1 + . + K xs ~ K xs (a, A
p(x)/P(x) ~ (a/A) xn-r ,
e quindi p(x)/P(x) se n>r, a/A se n=r, 0 se n<r
f ~ g loga f ~ loga g
se f discosta
da 1 (cioè |f-1| k > 0) in un intorno di c
, f(x) > 0, a >
(si possono prendere i logaritmi di entrambi i membri di una equivalenza asintotica, purché - sostanzialmente - non tendano, o comunque si avvicinino, a 1)
Esempio: Ch x ~ ex /2 per x log Ch x ~ log(ex /2) = x - log 2 ~ x
Controesempio: x2 ~ x per x 1, ma log x2 = 2 log x non è ~ log x.
f ~ g af ~ ag
se f è limitata nell'intorno di c , (a > 0).
(si possono prendere gli esponenziali di entrambi i membri di una equivalenza asintotica, purché - sostanzialmente - non tendano, o comunque si avvicinino, a
Controesempio: 1+x ~ x per x , ma e1+x / ex e
f(t) ~ g(t) per t b, h(x) b per x c, (con h(x) b per x c) f(h(x)) ~ g(h(x)) per x c.
(si possono eseguire cambiamenti di variabile in una equivalenza asintotica)
Esempi:
sin (x2) ~ x2 per x (b = 0, c = 0)
1-cos(3x)~9x2/2 per x (b = 0, c = 0)
log(1+5sin x) ~ 5x per x (b = 0, c = 0)
sin(1/x) ~ 1/x per x (b = 0, c =
sin(x) = sin (p - x) ~ (p - x) per x p (b = 0, c = p
log(cos x) = log(1+(cos x - 1)) ~ (cos x - 1) ~ -x2/2 per x (b = 0, c = 0)
8) In generale da f1 ~ g1 , f2 ~ g2 non segue f1 ± f2 ~ g1 ± g2.
Controesempio: f1(x) = x, f2(x) = sin x g1(x) = x+x , g2(x) = x per x 0: risulta
f1 - f2 = x - sin x ~ x3/6, che non è asintotico a g1 - g2 = x2.
La somma algebrica si può eseguire solo se non corrisponde ad una semplificazione delle parti principali (nel controesempio: x). Nel dubbio si utilizzi correttamente la nozione di "o piccolo". La formula di Taylor consente di scoprire come è fatto questo "o piccolo"
Esempi:
per x sin x ~ x , log(1+x) ~ x log(1+3x) + sin 2x ~ 3x + 2x = 5x,
per x 1 - cos x ~ Ch x - 1 ~ x2/2 Ch x - cos x ~ x2/2 + x2/2 = x2
per x ![]() ~ x
~ x ![]() + x ~ 2x, mentre
+ x ~ 2x, mentre
![]() - x non si può
trattare così semplicemente, ma richiede un passaggio in più. Raccogliendo la
potenza di grado massimo nel radicando, e sfruttando l'equivalenza asintotica
- x non si può
trattare così semplicemente, ma richiede un passaggio in più. Raccogliendo la
potenza di grado massimo nel radicando, e sfruttando l'equivalenza asintotica
(1 + t)a a t con a = 1/2 e t = -1/x si ha: ![]() - x = x ~ x/2 (- 1/x) = - ½ . Si noterà che
questo modo di procedere funziona altrettanto bene con radici di ordine
qualsiasi, con le quali non si può usare la tecnica di "razionalizzare alla
rovescia", moltiplicando e dividendo per la somma (
- x = x ~ x/2 (- 1/x) = - ½ . Si noterà che
questo modo di procedere funziona altrettanto bene con radici di ordine
qualsiasi, con le quali non si può usare la tecnica di "razionalizzare alla
rovescia", moltiplicando e dividendo per la somma (![]() + x). Ad es.,
+ x). Ad es., ![]() - x ~ x (1/5) (- 1/x4) = - 1/(5x3),
mentre
- x ~ x (1/5) (- 1/x4) = - 1/(5x3),
mentre ![]() - x ~
- x ~
~ x (1/5) (- 1/x) = - 1/5.
9) f ~ g , g > 0 " e > un intorno di c in cui valgono le disuguaglianze:
e) g(x) < f(x) < e) g(x). Se g < 0,
si ha analogamente (1+e) g(x) < f(x) < e) g(x).
Queste disuguaglianze significano che il grafico di f(x), in un intorno di c, è compreso tra quelli di (1-e) g(x) e di (1+e) g(x). L'osservazione
è molto significativa quando g(x) 0 per x c.
Siano f e g come nel paragrafo precedente. Si dice allora che f è "o piccolo" di g (per x c), e si scrive f(x) = o(g(x)), oppure brevemente, f = o(g), se avviene che:
![]() .
.
La relazione di "o piccolo" non è una relazione di equivalenza non essendo riflessiva (difatti f = o(f) è sempre falsa). Inoltre essa non è né simmetrica né antisimmetrica (le due relazioni f = o(g) e g = o(f) sono fra loro incompatibili). Vale soltanto la proprietà transitiva: f = o(g) e g = o(h) f = o(h).
Si noti che, nonostante la scrittura f = o(g), "o" non è una funzione, ma solo un simbolo indicante un ordine di grandezza.
Valgono inoltre le seguenti proprietà:
f = o(1) lim f(x) = 0
f = g + o(h) significa f - g = o(h)
f ~ g f = g + o(g) f - g = o(g)
f = o(g), g ~ h f = o(h)
f o(g) = o(f g)
k costante o(kg) = o(g)
Esempi:
a) per x
x3 = o(x2) x2 = o(x) x = o(1) 1 = o(1/x) .
e, in generale, xb = o(xa), a < b reali (anche negativi!)
nel polinomio p(x) = a xn + b xn-1 + . + k xm tutti i termini sono "o piccolo" di quello con la potenza minore
log x = o(1/x) (equivale a x log(x) = o(1), cioè x log(x)
b) per x
1/x2 = o(1/x) 1/x = o(1) 1 = o(x) x = o(x2) x2 = o(x3) .
e, in generale, xa = o(xb), a < b reali (anche negativi!)
nel polinomio p(x) = a xn + b xn-1 + . + k xm tutti i termini sono "o piccolo" di quello con la potenza maggiore
e-x = o(1/xn) " n > 0 o, equivalentemente, xn = o(ex)
log x = o(xa) " a > 0
log (log x) = o(log x) log (log (log x)) = o(log (log x)) ..
e-2x = o(e-x) ![]() " a R
" a R
A) Calcolo di limiti e grafico di funzioni
Si ricorda che le funzioni y = xa per x 0+ presentano tangente verticale se 0 < a < 1, orizzontale se 1 < a. Prolungate a sinistra dell'origine in modo simmetrico rispetto all'asse y (rendendole cioè funzioni pari) tramite y = |x|a, esse presentano, per 0 < a < 1, una cuspide a tangente verticale. Prolungate in modo simmetrico rispetto all'origine (funzioni dispari) tramite la posizione y = |x|a sgn(x), esse presentano, per 0 < a < 1, un flesso a tangente verticale. Si ricorda inoltre che y = |x| presenta nell'origine un punto angoloso.
(Se a è un esponente razionale, a = p/q, con q dispari, le funzioni sono già definite per x < 0 e risultano pari se p è pari, dispari se p è dispari). Lo stesso comportamento avrà dunque una funzione asintoticamente equivalente ad una potenza con esponente a
Per x
1) ![]()
2) 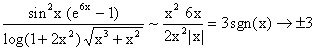 (per x
(per x
3)
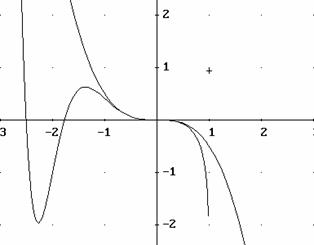
![]() Se ne deduce non solo che tale funzione tende a 0, ma anche
che il suo grafico presenta nell'origine un flesso orizzontale discendente
(vedi figura).
Se ne deduce non solo che tale funzione tende a 0, ma anche
che il suo grafico presenta nell'origine un flesso orizzontale discendente
(vedi figura).
4)
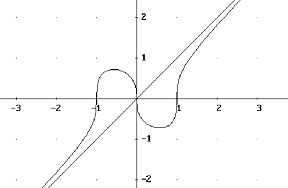
f(x) = ![]() per x 0 è ~ -x1/3,
ed ha quindi un flesso verticale nell'origine (con derivata "- "). Analogamente per x 1 risulta f
~ [2(x-1)]1/3 e per x -1 risulta f ~ [2(x+1)]1/3. Dunque anche in ±1 vi
sono dei flessi verticali. Per x è invece f ~ x, f - x = = x
~ x (- 1/2x2) = = - 1/2x 0, dunque f presenta l'asintoto obliquo y = x.
per x 0 è ~ -x1/3,
ed ha quindi un flesso verticale nell'origine (con derivata "- "). Analogamente per x 1 risulta f
~ [2(x-1)]1/3 e per x -1 risulta f ~ [2(x+1)]1/3. Dunque anche in ±1 vi
sono dei flessi verticali. Per x è invece f ~ x, f - x = = x
~ x (- 1/2x2) = = - 1/2x 0, dunque f presenta l'asintoto obliquo y = x.
5)
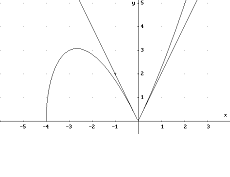
f(x) = ![]() . Tenendo conto delle equivalenze già indicate al punto 3) di
pag. 2, si ha il grafico in figura.
. Tenendo conto delle equivalenze già indicate al punto 3) di
pag. 2, si ha il grafico in figura.
B) Asintoto obliquo
La linea di equazione y = f(x) ammette la retta y = mx + q (m 0) come asintoto obliquo (per x ) se risulta f(x) = mx + q + o(1) (per x ). Si ha pertanto f(x) ~ mx + q ~ mx, da cui
m = lim f(x)/x q = lim [f(x) - mx]
Risulta pure, per la regola di De L'Hôpital, m = lim f '(x) (se tale limite esiste).
È improprio scrivere f(x) ~ mx + q , dato che tale espressione equivale solo a f(x) = mx + o(x).
(Controesempi: f = x + log x; f = x + sin x che non presentano asintoti obliqui pur essendo ~ x).
C) Formula di Taylor
Sia f continua in un intorno di c con tutte le sue derivate fino all'ordine n [risp. (n+1)]. Allora valgono le seguenti relazioni, che traducono la cosiddetta formula di Taylor (con il resto di Peano)
f(x) = ![]() f (k)(c) (x-c)k /k! + o[(x-c)n
]
f (k)(c) (x-c)k /k! + o[(x-c)n
]
f(x) - ![]() f (k)(c) (x-c)k /k! ~ f (n+1)(c)
(x-c) n+1/(n+1)! (se f (n+1) (c) 0).
f (k)(c) (x-c)k /k! ~ f (n+1)(c)
(x-c) n+1/(n+1)! (se f (n+1) (c) 0).
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025