Teorema del minimo negli N

Se A N allora A ha minimo. (dim. sempl.)

Teorema sul M.C.D. negli N

Siano a,b,d N; Sono equivalenti:

d|a, d|b, " c N se c|a e c|b c|d

d = MCD(a,b)

Dimostrazione:

Supponiamo d' = MCD(a,b) quindi d'|a, d'|b  d'|d d' d, ma siccome d' MCD non puo' essere <, allora d'=d.

1 (cfr. Algoritmo Euclideo)

Algoritmo Euclideo

Dati a,b N a b e a>b>1 b 0 (MCD immediato)

Allora a=qb+r

Se r=0 (a,b) = b

Altrimenti r>0: b=q₁r+r₁ Se r₁=0 termina l' algoritmo.

Altrimenti r₁>0 r=q₂r₁+r₂ ......

Questo procedimento ha termine e in particolare:

b>r₁>r₂>.>r_n=0. La successione dei resti termina con lo zero (questo avviene perché abbiamo un ordine decrescente e ci troviamo negli N dove vale il teorema del minimo).

Se n e tale che r_n = 0 allora il MCD sarà r_n-1 perché ((a,b)=(b,r₁)=(r₁,r₂)=.=(r_n-1,r_n)=r_n-1 poiché r_n=0).

Le grandezze per cui ha termine quest' algoritmo sono dette commensurabili (altrimenti sono dette incommensurabili).

Primo teorema di Euclide

Se p N è primo e p|ab p|a o p|b o p divide entrambi; se p non divide a (p,a)=1

Teorema degli MCD negli Z

Siano a,b Z e a,b 0. Il d=(a,b) esiste ed è unico e d>0. Inoltre esistono w,z Z tali che aw+bz=d. 939f52j

Dimostrazione:

Consideriamo S=, allora prendiamo l' elemento minimo dell' insieme (esiste perché S N e m 0) e lo chiamiamo d. Adesso dobbiamo provare che d|a e d|b.

Supponiamo che d non divide a, allora a=qd+r con 0 r < d.

Noi sappiamo però che d=aw+bz (con w,z Z perché d S),

quindi r=a-qd=a-q(aw+bz)=a(1-qw)+b(-qz) r S e r<d

Siccome avevamo supposto d elemento minimo di S, allora r=0 e a=qd ossia d|a. Similmente si puo' provare che d|b.

Per dimostrare che d=(a,b), devo far vedere che " c Z con c|a e c|b allora c|d. Ho che a=cn e b=cm, allora d=aw+bz=c(nw+mz) quindi c|d.

Insiemi

Insieme delle parti di A: Dato A insieme si dice che P(A) è l' insieme delle parti di A se è l'insieme dei sottoinsiemi di A.

Partizione di A: Dato A insieme si dice F partizione di A con F=_{i I} X_i A e F P(A) se:

" X_i F X_i

" i,j I con i j X_i X_j=

_{i I}X_i = A

Prodotto cartesiano: Si definisce prodotto cartesiano di A₁xA₂x.xA_n l' insieme delle n-uple (a₁,a₂,.,a_n) ove a_i A_i "i=1,.,n.

Corrispondenza: Una corrispondenza definita da A su B e un sottoinsieme del prodotto cartesiano AxB.

Applicazione: Un' applicazione f di A su B è una particolare corrispondenza che associa " a A un unico b tale che (a,b) f. Può essere:

Iniettiva Se " a,b A con f(a)=f(b) a=b.

Suriettiva Se " b B esiste a A tale che f(a)=b.

Biettiva) Se iniettiva e suriettiva.

Si dicono f(A)=B' immagine dell' applicazione f mentre f ^-1(B') si dice controimmagine di B'.

Proposizione 3.1: L' applicazione composta di due funzioni iniettive (rispettivamente suriettive, biiettive) è iniettiva (suriettiva,biiettiva). Non vale il viceversa.

Applicazione identica: I_a:A->A  I_a(a)=a "a A.

La composizione di applicazione gode della proprietà associativa

f ° (g ° h)= (f ° g) ° h=f ° g ° h.

Teorema: Siano g,g₁,g₂:B->C e f,f₁,f₂:A->B applicazioni:

a)  Se g₁°f=g₂°f e f è suriettiva g₁=g₂

b)  Se g°f₁=g°f₂ e g è iniettiva f₁=f₂.

Dimostrazione:

a)  Per la suriettività di f abbiamo che "b B esiste un a A tale che f(a)=b. "b B sappiamo quindi che  g₁(f(a))=g₁(b) e g₂(f(a))=g₂(b)

ma per ipotesi g₁°f(a)=g₂°f(a) g₁(b)=g₂(b).

b)  Per la iniettività di g abbiamo che "b,b' B g(b)=g(b') sse b=b'. Noi dobbiamo provare che "a A f₁(a)=f₂(a). Supponiamo per assurdo che f₁(a)=b e f₂(a)=b' con b b'.

Allora avremmo che     g°f₁(a)=g(b),

e   g°f₂(a)=g(b'),

ma avevamo supposto "a A g°f₁(a)=g°f₂(a), quindi g(b)=g(b') assurdo per l'iniettività di g.

Teorema: Siano f:A->B e g:B->C due applicazioni:

a)  Se g°f è iniettiva f è iniettiva

b)  Se g°f è suriettiva g è suriettiva.

Dimostrazione:

a)  Dobbiamo far vedere che " a,a' A se abbiamo f(a)=f(a') allora a=a'. Supposto f(a)=f(a') ho che g(f(a))=g(f(a')) quindi g°f(a)=g°f(a'), che per l'iniettività supposta a=a'.

b)  Dobbiamo far vedere che " c C abbiamo almeno un b B tale che g(b)=c. Noi sappiamo per la suriettività di g°f che " c C esiste a A che verifica c=g°f(a). Ma g°f(a)=g(f(a)) e ponendo b=f(a) allora vediamo che "c si ha c=g(f(a))=g(b).

Teorema: Sia f:A->B un'applicazione, sono equivalenti:

a)  Esiste un' applicazione g:B->A tale che f°g=i_b

b)  f è suriettiva.

Dimostrazione:

a) b) Dobbiamo dimostrare che " b B esiste almeno un a A tale che f(a)=b. Per la suriettività di i_b sappiamo che " b B esiste un elemento b' B tale che b=f°g(b'), ma f°g(b') = f(g(b')), se noi poniamo a=g(b') vediamo che " b B esiste a tale che f(g(b'))=f(a)=b.

b) a) f è suriettiva e quindi " b B esiste a A tale che f(a)=b. La funzione g sarà definita in questo modo: "b B prendo un a A ponendo g(b)=a sse f(a)=b.

Proposizione 3.2: Sia f:A->B una applicazione. Allora se esistono g,h:B->A applicazioni tali che f°g=i_b e h°f=i_a g=h.

Dimostrazione:

h=h°i_b=h°(f°g)=(h°f)°g=i_a°g=g

Proposizione 3.3: Una applicazione f:A->B è biiettiva sse esiste una applicazione g:B->A tale che g°f=i_a e f°g=i_b.

Dimostrazione:

) Siccome i_a è iniettiva, allora per un teorema precedente f è iniettiva, siccome i_b è suriettiva, per lo stesso teorema, f è anche suriettiva e quindi biiettiva.

) Siccome f è suriettiva, allora " b B esiste un a A tale che f(a)=b, che per l'iniettività di f è unico. Posso definire una funzione g:B->A in questo modo: " b B g(b)=a sse f(a)=b, cosi avrei che " b B f°g(b)=f(g(b))=b=i_b(b) e " a A g°f(a)=g(f(a))=a=i_a(a).

Applicazione inversa: Per ogni applicazione biiettiva f, l' applicazione inversa g è definita " a A e b B g(b)=a sse f(a)=b.

Proposizione 3.4: Date f e g due applicazioni biiettive, allora (f ^-1)^-1=f e (f ° g )^-1 = g ^-1 ° f ^-1.

Relazione: Una relazione R su A è una corrispondenza di A su A. Si dice:

Riflessiva) se "a A a R a

Simmetrica) se "a,b A  a R b b R a

Transitiva) se " a,b,c A  a R b, b R c a R c

Se valgono le tre proprietà allora R si dice di equivalenza.

Classe di equivalenza di a A: l' insieme [a]~ = (con ~ equivalenza su A)

Insieme quoziente di A modulo ~: l'insieme A/~ = (con ~ equivalenza su A)

Applicazione canonica: L' applicazione p:A->A/~, così definita: "a A p(a)=[a]~.

Teorema

Sia A un insieme non vuoto, allora:

a)  Se ~ è una equivalenza su A, allora A/~ è una partizione di A.

b)  Se F è una partizione di A, allora è possibile definire un' equivalenza ~ su A ponendo x~y con x,y A se esiste X F tale che x,y X.

Dimostrazione

a)

" [a]~ A/~ [a]~

Ovvia a [a]~.

" [a]~,[b]~ A/~ con [a]~ [b]~ [a]~ [b]~=

Se [a]~ [b]~ allora c'è almeno un elemento x tale che x [a]~ [b]~

x [a]~ a~x

x [b]~ b~x x~b ma allora a~b e quindi [a]~=[b]~ assurdo.

_{a A}[a]~ = A

Ovvia perché _{a A}[a]~ A e _{a A}[a]~ A. Ogni elemento x A appartiene ad una classe (x [x]~).

b)

riflessiva: "a A a a. "a A esisterà un X F tale che a X, quindi a a.

simmetrica: "a,b A a b sse b a

"a,b A se a b allora esiste X F tale che a,b X. Ma allora anche b a

transitiva: "a,b,c A a b,b c a c

"a,b,c se a b significa che esiste X F tale che a,b X. Ma se b c allora esiste W F tale che b,c W. Siccome F è una partizione abbiamo che X W= , allora X=W.

Teorema di fattorizzazione delle applicazioni tra insiemi

Siano A,B insiemi e f:A->B un' applicazione, una equivalenza definita su A in questo modo: x,y A x y sse f(x)=f(y); e sia p:A->A/ la sua proiezione canonica, allora:

a)  esiste ed è unica l'applicazione f :A/ ->B tale che rende commutativo il diagramma

(ovvero tale che f p=f)

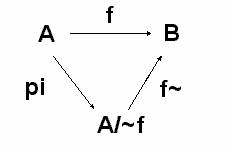
b)  f è iniettiva

c)  f è biiettiva sse f è suriettiva.

Dimostrazione:

a)  Esistenza: Definendo f :A/ ->B nel seguente modo: f ([a])=f(a), allora f è ben definita perché " a A si ha f p(a)=f ([a])=f(a)

Unicità: Supponiamo esista una g tale che g p=f p

allora "a A abbiamo g p(a)=g p(a))=g ([a])=f(a),

ma anche f p(a)=f(a), quindi g =f "a A.

b)  Iniettività di f : Devo dimostrare che " [a],[b] A/ f ([a])=f ([b]) sse [a]=[b],

supponiamo per assurdo che [a] [b] e f ([a])=f ([b]),

io so che f ([a])=f(a) e f ([b])=f(b), e siccome f ([a])=f ([b]), allora f(a)=f(b),

ma allora a b, quindi p(a)=p(b)=[a]=[b] assurdo.

c)  Biiettività di f

Se f è biiettiva, allora f=f p composta da due applicazioni suriettive è suriettiva.

Se f è suriettiva, allora " b B esiste a A tale che f(a)=b,

quindi "b B esiste a A tale che f p(a)=b,

quindi "b B esiste [a] A/ ([a]=p(a)) tale che f ([a])=b,

quindi f è suriettiva e iniettiva f biiettiva.

Teorema: Siano A insieme e R,R' relazioni di equivalenza su A, le due affermazioni sono equivalenti:

a)  R=R'

b)  A/R=A/R'

Dimostrazione:

a)  Ovvia perché se R=R', allora "a,b A si ha che se aRb aR'b e quindi [a]R = [a]R' ma allora A/R = A/R'.

b)  Siccome A/R=A/R', allora A/R==A/R'=, quindi "a A si ha [a]R=[a]R' "a,b A se aRb allora aR'b R=R'.

Insieme delle classi resto

Siano a,b Z, si dice che a e b sono congrui modulo n (a _nb) se n|(a-b). La congruenza è una relazione di equivalenza su Z. E' possibile quindi formare l' insieme Z_n come

Z_n=Z/ _n

Si nota che [a]=[b] con [a],[b] Z_n sse a _nb. E si nota anche che

[a]= [a]= [a]= [a]=

La classi di congruenza sono compatibili con somma e prodotto così definiti:

[a]_n+[b]_n=[a+b]_n

[a]_n[b]_n=[ab]_n

Casi speciali:    ) coincide con = (0 divide solo 0, quindi a-b=0 a=b "a,b Z)

) coincide con la relazione banale w (1 divide tutti i numeri Z Z_n ha una sola classe che contiene tutto Z)

Lemma 8.1

Se fisso un numero n 1 e considero _n allora gli elementi di Z_n sono , ed in particolare sono n e sono distinti.

Dimostrazione:

Devo dimostrare che ho n elementi, allora dimostro che se prendo un qualunque elemento [a] allora [a] Z_n. Se a Z allora a [a], se divido a per n avrò a=qn+r, ma allora nq=a-r e quindi r _na e questo implica a [r]. Visto che 0 r<n allora [r] Z_n [a]=[r] Z_n.

Adesso dimostro che gli elementi sono distinti. Devo dimostrare che presi due interi 0 i<j n-1, avrò che [i] [j]. Io ho che 0<j-i<n, quindi i e j non sono congrui mod n (perché n non divide un numero < di n), allora apparterranno a classi distinte.

Proprietà di Z_n

Proprietà associativa (+,*).

Proprietà commutativa (+,*).

Esistenza el. neutro ([0] e [1]).

Proprietà distributiva della somma rispetto al prodotto ([a]+[b])*[c]=[a]*[c]+[b]*[c].

Proprietà di cancellazione della somma [a]+[b]=[a]+[c] [b]=[c]

Esistenza dell' elemento opposto [a]+[n-a]=[0]

Se n è un numero primo allora valgono anche

Proprietà di cancellazione del prodotto [a]*[b]=[a]*[c] [b]=[c].

Legge di annullamento del prodotto [a]*[b]=[0] [a]=0 o [b]=0.

Esistenza dell' elemento inverso [a]*[a^-1]=[a^-1]*[a]=[1].

Relazione antisimmetrica: Quando relazione su A "a,b A se a b e b a allora a=b.

Ordine parziale su un insieme A: Una relazione che gode delle proprietà riflessiva, antisimmetrica e transitiva. L' insieme A si dirà parzialmente ordinato (A,

Ordine totale su un insieme A: Una relazione di ordine parziale su A tale che "a,b A si ha a b oppure b a. L' insieme A si dirà totalmente ordinato (A,

Esempi (N*,|) è un ordine parziale (non totale perché esistono a,b N* tali che a|b e b|a), mentre (N, ) è un ordine totale perché "a,b N a b o b a).

Omomorfismo di insiemi ordinati: Siano (A, ) e (A', ') insiemi parzialmente ordinati. Un' omomorfismo di insiemi ordinati è un applicazione f:A->A' tale che x y f(x) 'f(y) "x,y A.

LEMMA 10.1

Siano (A, ) e (A', ') due insiemi parzialmente ordinati e f:A->A' una biiezione. Allora le seguenti affermazioni sono equivalenti:

a)  entrambe le applicazioni f e f ^-1 sono omomorfismi di insiemi ordinati.

b)  "x,y A x y sse f(x) 'f(y)

Isomorfismo di insiemi ordinati : Una applicazione biiettiva (fra due insiemi parzialmente ordinati) che soddisfi una delle due affermazioni del lemma precedente. Gli insiemi A e A' si diranno isomorfi.

Sottoinsieme ordinato: B A con (A, ) parzialmente ordinato, risulta anch'esso un insieme parzialmente ordinato. Si dirà che l'ordinamento di A ha indotto un ordinamento su B, oppure B è una restrizione dell' ordinamento parziale di A.

Esempi

Siano (N*,|) e (N*, ) due insiemi ordinati e I_N*:N*->N* l'applicazione identica che va da N* ordinato da | a N* ordinato da . I_N* è un omomorfismo di insiemi ordinati (se x,y N* e x|y x y), ma non un isomorfismo (perché esiste x,y t.c. x y ma x non divide y).

Se consideriamo il sottoinsieme ordinato B= N* allora f:N*->B con f(a)=2^a "a N* considerando (N*, ) e (B,|) è un isomorfismo di insiemi ordinati.

Definizioni: Sia (A, ) un insieme parzialmente ordinato

Minimo:a A tale che "x A a x.

Massimo:a A tale che "x A x a.

Minimale:a A tale che se "x A si ha x a x=a.

Massimale:a A tale che se "x A si ha a x x=a.

Minorante:B A a A si chiama minorante di B se "x B si ha a x.

Maggiorante:B A a A si chiama maggiorante di B se "x B si ha x a.

Estremo inferiore: (di B A) Massimo dell' insieme dei minoranti di B.

Estremo superiore: (di B A) Minimo del' insieme dei maggioranti di B.

Insieme bene ordinato: Se ogni sottoinsieme non vuoto di un insieme parzialmente ordinato ha minimo, allora questo insieme è bene ordinato. Un' insieme bene ordinato è  totalmente ordinato.

Equipotenza: A è equipotente a B se esiste una biiezione f:A->B.

Insieme finito: A è finito se contiene un numero finito di elementi. Questo numero si dice cardinalità di A (|A|).

A e B insiemi finiti disgiunti |A B|= |A|+|B|,

non necessariamente disgiunti |A B| +|A B| = |A|+|B|,

|AxB| = |A|*|B|,

|B^A|=|B|^|A|.

Insieme numerabile: A è numerabile se ha la stessa cardinalità di N.

Insieme infinito: A è infinito sse

a)  è equipotente ad un suo sottoinsieme proprio,

b)  contiene un suo sottoinsieme proprio numerabile.

Insieme continuo: A è continuo se ha la stessa cardinalità di R.

Insieme discreto: A è discreto se è finito o numerabile.

Teorema

Siano A e B due insiemi, è sempre possibile trovare o una applicazione iniettiva da A in B, o una applicazione iniettiva da B in A, o entrambe.

Teorema di Cantor-Beirnstein

Dati A,B insiemi, se esiste f:A->B' iniettiva B' B e g:B->A' iniettiva con A' A, allora esiste una applicazione biiettiva da A in B. (Sono equipotenti).

Teorema 1.2

Se A è un' insieme allora |P(A)|>|A|.

Teorema 1.3

Se A è un' insieme allora |P(A)|=|^A|.

Teorema 1.4

Se A,B,C,D sono insiemi, e se |A|=|C| e |B|=|D|, allora |B^A|=|D^C|.

Teorema 1.5

L'unione di una famiglia numerabile di insiemi numerabili è numerabile.

Teorema 1.6

Se A è un insieme infinito, allora è |A|=|Aⁿ| "n N con n

Teorema 1.8

Ogni sottoinsieme B N_n è finito

Teorema 1.9

Ogni sottoinsieme B N è finito o numerabile. (Più in generale, ogni sottoinsieme di un insieme numerabile è finito e numerabile).

Teorema 1.10

Ogni sottoinsieme di un insieme finito è un insieme finito.

Z e Q sono numerabili

R non è numerabile

Teorema 1.16 (Principio dei cassetti)

Siano A e B insiemi finiti rispettivamente di cardinalità m e n, con m>n. Allora non esistono applicazioni iniettive f con f:A->B. (Se distribuisco m oggetti in n cassetti, allora avrò almeno un cassetto con almeno 2 oggetti).

Dimostrazione: Si dimostra con il principio di induzione su n.

Caso base) n=0. Ovvio, non possono esistere applicazioni da A su B, tantomeno applicazioni iniettive. (Devi dire anche che non esistono applicazioni perché si suppongono A e B non vuoti! !)

Caso induttivo) Suppongo l'enunciato vero per un insieme H di cardinalità n-1 1, adesso devo provarlo su B con cardinalità n. Io ho |A|=m>n. Data f:A->B (può esistere in quanto B ha almeno un elemento), bisogna provare che f non è iniettiva. L'insieme im(f), non è vuoto, quindi esisterà un elemento b B tale che f(a')=b. Allora adesso pongo H=B- e considero l'applicazione g

g:A-->H definita come g(a)=f(a) "a A-.

|A-|=|A|-||=m-1 e |H|=|B-|=|B|-||=n-1, siccome m>n allora m-1>n-1, che rientra nell' ipotesi induttiva, g non è iniettiva (questo caso si riferisce ad una g supposta applicazione, prima gli devi far vedere i tre casi in cui g potrebbe non essere un' applicazione e far vedere che in tutti i tre casi f non è iniettiva, prova a guardare gli appunti di tinaglia). Esiste a,c A- con a c tali che g(a)=g(c), e ovviamente f(a)=f(c), quindi anche f non è iniettiva.

Teorema 1.18

Siano A e B insiemi finiti rispettivamente di cardinalità m e n con m<n. Allora non esistono applicazioni f:A->B suriettive.

Dimostrazione:

Si dimostra per induzione su m.

Caso base |A|=m=0

In questo caso per la definizione di applicazione non possono esistere applicazioni f:A->B, tantomeno applicazioni suriettive.

Caso induttivo

Supposto l' enunciato vero per insiemi H con |H|=m-1, allora dobbiamo verificare che sia valido anche per insiemi A con |A|=m. Ovvero dobbiamo dimostrare che data una qualunque f:A->B applicazione, allora f non è suriettiva.

Considerata una f qualunque applicazione da A su B, prendo un elemento b B tale che f^-1(b) . Adesso considero gli insiemi H=A-f^-1(b) e B'=B-, e la corrispondenza g:H->B' definita "a H g(a)=f(a). Questa g è un applicazione. Per l' ipotesi induttiva g non può essere suriettiva, perché |A-f^-1(b)|=|A|-|f^-1(b)|=m-i con 1 i m-i m-1<n-1 perché m<n. Allora esiste b' B' t.c. g^-1(b')= . Supponiamo per assurdo che esista a A t.c. f(a)=b', allora o a H oppure a f^-1(b). Se a H, allora f(a)=b'=g(a) per come abbiamo definito g, ma avevamo detto che g^-1(b')= . Se a f^-1(b), allora f(a)=b ma f(a)=b', quindi f non sarebbe applicazione ASSURDO esiste b' B t.c. f^-1(b')= , quindi f non può essere suriettiva.

Teorema 1.19

Siano  A e B insiemi finiti di cardinalità n, e se f:A->B è un' applicazione le seguenti affermazioni sono equivalenti:

a)  f è iniettiva

b)  f è suriettiva

c)  f è biunivoca

Dimostrazione: basta dimostrare a b e b a, visto che a,b c e c a,b.

a b) Per assurdo, se f non è suriettiva, allora esiste un b B, tale che la sua controimmagine di f è vuota. Se considero H=B- e la funzione g:A->H definita come g(a)=f(a) "a A, allora posso vedere che |A|=n e |H|=n-1. Per il teorema 1.16 g non può essere iniettiva e come conseguenza neanche f, allora si è raggiunto l' assurdo.

b a)Per assurdo, se f non è iniettiva, avremo a,a' A con a a', tali che f(a)=f(a').Se considero H=A-, e la funzione g:H->B definita come g(a)=f(a) "a H, allora posso vedere che |H|=n-1 e |B|=n. Per il teorema 1.18 g non può essere suriettiva, come conseguenza neanche f: assurdo.

Calcolo combinatorio

n-fattoriale: Il fattoriale di n, è il prodotto di tutti i numeri naturali da n a 1, n!=n(n-1)! , 1!=1 e 0!=1.

Disposizioni con ripetizioni

Una disposizione con ripetizioni di classe m degli n oggetti di A è un' applicazione f:B->A essendo B un insieme tale che sia |B|=m.

Proposizione 1: Il numero delle disposizioni con ripetizione di classe m di n elementi è D'_n,m=n^m.

Proposizione 2: Se A e B sono insiemi finiti e se |A|=n e |B|=m allora si ha |A^B|=|A|^|B|=n^m.

Disposizioni semplici

Una disposizione semplice di classe m degli n oggetti di A è un' applicazione iniettiva f:B->A ove B è un insieme con |B|=m (B=N_m).

Proposizione 1: Il numero delle disposizioni semplici di classe m di n elementi è

D_n,m=(n)_m= n!/(n-m)!

Proposizione 2: Se A e B sono insiemi finiti e se |A|=n e |B|=m con m n il numero delle applicazioni iniettive f:B->A è:

D_n,m=(n)_m= n!/(n-m)!

Permutazioni

Sia A un insieme finito e sia |A|=n.

I^a definizione: Si chiamano le permutazioni degli n oggetti di A, le disposizioni semplici di classe n degli n oggetti di A.

II^a definizione: Una permutazione degli n oggetti di A è un' applicazione biunivoca f:B->A essendo B un insieme che sia |B|=n. Di solito si prende B=N_m.

III^a definizione: Una permutazione di A è un' applicazione biunivoca f:A->A.

Corollario: Il numero delle permutazioni di n elementi è P_n=n!.

Combinazioni semplici

Sia A finito, |A|=n e sia m n m N.

I^a definizione: Si chiamano combinazioni semplici di classe m degli n oggetti di A i raggruppamenti con m degli n oggetti di A tale che due raggruppamenti sono diversi se hanno elementi diversi. Si osservi che i raggruppamenti con gli stessi elementi danno la stessa combinazione.

II^a definizione: Una combinazione semplice di classe m degli n oggetti di A è un sottoinsieme B A con |B|=m.

III^a definizione: Una combinazione semplice di classe m degli n oggetti di A è l' immmagine im(f) di un' applicazione iniettiva f:B->A essendo B un insieme con |B|=m. (Di solito B=N_m).

Proposizione 1:Il numero delle combinazioni semplici di classe m di n elementi (m n) è

n

=D_n,m/m!=n!/[m!(n-m)!]

m

Coefficenti binomiali: I numeri naturali

n

k

si chiamano coefficenti binomiali.

Godono delle seguenti proprietà:

n n

=

k n-k

n n-1 n-1

= +

k k k-1

3. Se n è un numero primo e se k è un naturale tale che 1 k n-1 allora n divide n

k

Dimostrazione:

n n

= n!/((n-k)!(n-(n-k)!))=n!/[(n-k)!k!]=

k n-k

Guardatele sulle dispense.

Numero di stirling di seconda specie: S(n,m) è il numero delle partizioni di A con m sottoinsiemi.

S(n,1)=1 e S(n,n)=1

Se si conosce il numero S(n,m) per un m tale che 2 m n-1 allora

|P(A)|=2+S_m=2.n-1 S(n,m) dove S(n,m)=mS(n-1,m)+S(n-1,m-1) (ricorsiva).

Strutture Algebriche

Operazione: Si dice operazione su A, una applicazione w:AxA->A. (Si chiama anche legge di composizione).

Sottoinsieme chiuso: Dato A insieme e * un' operazione su A, allora B A con la proprietà che se "a,b B si ha a*b B, allora B si dice sottoinsieme chiuso per l'operazione *. In questo caso * induce un operazione BxB->B definita come (a,b)->a*b "a,b B.

Struttura algebrica: Si definisce struttura algebrica, un insieme A dotato di un operazione * e si denota (A,*).

Identità sx (dx): Sia (S,*) un semigruppo, un' identità sx (dx) di S è un elemento e S tale che ea=e (ae=a) "a S. Se e S è identita sx e dx, allora e si dice elemento neutro.

Gruppo: La struttura algebrica (G,*) si definisce gruppo quando valgono le segueti proprietà:

Proprietà associativa; "a,b,c G si ha a*(b*c)=(a*b)*c.

Esistenza dell' elemento neutro; e G tale che "a G si ha a*e=e*a=a.

Esistenza dell' inverso; "a G esiste b G tale che a*b=b*a=e.

Se inoltre vale la proprietà commutativa; "a,b G si ha a*b=b*a, allora (G,*) si dice gruppo abeliano o commutativo.

Semigruppo: Struttura algebrica in cui vale solo la proprietà 1.

Monoide : Struttura algebrica in cui valgono solo le proprietà 1 e 2.

Se T è un sottoinsieme chiuso rispetto ad un gruppo (semigruppo,monoide) (G,*), allora (T,*) è un sottogruppo (sottosemigruppo, sottomonoide). Si indica T G.

L'ordine di un gruppo è la cardinalità del gruppo.

Data la struttura (A,*) con a A e n N si definisce per induzione la potenza n-esima aⁿ di a:

Semigruppo: "n N- aⁿ=a^n-1*a e a¹=a.

Monoide:     n=0 a⁰=e.

"n N- aⁿ=a^n-1*a e a¹=a.

Gruppo: "n Z

a^n-1*a    se n>0

aⁿ = e   se n=0

(a^-1)^-n    se n<0.

Data la struttura (A,+) con a A e n N si definisce per induzione il multiplo n-esimo na di a:

Semigruppo: "n N- na=(n-1)a+a e 1a=a.

Monoide:     n=0 0a=0.

"n N- na=(n-1)a+a e 1a=a.

Gruppo: "n Z

(n-1)a+a   se n>0

na = e   se n=0

(-a)(-n) se n<0.

In un gruppo G l'elemento neutro è unico

Dimostrazione:

Supponiamo e ed e' due elementi neutri allora:

e G "a G e*a=a*e=a e*e'=e'*e=e'

e'=e'*e=e.

e' G "a G e'*a=a*e'=a e'*e=e*e'=e

In un gruppo G l' elemento inverso è unico.

Dimostrazione:

Dato a G supponiamo che esistano be b' due inversi, allora:

a*b=b*a=e

b'=b'*e=b'*(a*b)=(b'*a)*b=e*b=b

a*b'=b'*a=e

Teorema

Sia (G,*) gruppo a,b G, allora a*b è invertibile e (a*b)^-1=b^-1*a^-1.

Dimostrazione:

esistenza)     esiste b^-1 G tale che b^-1*b= b*b^-1=e.

esiste a^-1 G tale che a^-1*a= a*a^-1=e.

esiste anche (a*b)^-1 G (a*b)*(a*b)^-1=(a*b)^-1*(a*b)=e

esiste b^-1*a^-1 G

uguaglianza) (a*b)*(b^-1*a^-1)=a*(b*b^-1)*a^-1=a*e*a^-1=a*a^-1=e

(b^-1*a^-1)*(a*b)=b^-1*(a^-1*a)*b=b^-1*e*b=b^-1*b=e

(a*b)^-1=b^-1*a^-1.

Teorema

Sia (M,*) un monoide, se considero S M insieme degli elementi invertibili di M (S,*) è un gruppo.

Dimostrazione: S è ancora una struttura, perché il prodotto di due elementi invertibili è ancora un elemento invertibile (ho dimostrato che S è chiuso per l' operazione ). 1_M S, perché è un elemento invertibile di M, e "a S esiste b tale che ab=b*a=e (esiste l' inverso), per come è stato definito S.

Teorema

Sia H G con (G,*) gruppo e H . Allora sono equivalenti:

a)  H è sottogruppo di G

b) 

H è sottoinsieme chiuso per l'operazione *

1_G H.

"a H a^-1 H.

Dimostrazione:

a b) 1,3 ovvie per definizione di sottogruppo. Supponiamo 1_H 1_G, allora "a H a*1_H=1_H*a=a e a*1_G=1_G*a=a esistenza di 2 elementi neutri che porta ad un' assurdo: quindi 1_H=1_G.

b a)Devo dimostrare che "a,b,c H si ha a*(b*c)=(a*b)*c, che è vero perché a,b,c G. Devo anche dimostrare che a*(b*c) H, ma è immediato per il punto 1.

Teorema

Sia H G con (G,*) gruppo e H . Allora sono equivalenti:

a)  H è sottogruppo di G

b)  H e "a,b H a*b^-1 H.

Dimostrazione:

a b)Ovvia per la chiusura di H rispetto a *.

b a)   Dimostro che 1_G H:

se a H a*a^-1 H 1_G H.

Dimostro che "a H esiste a^-1 H tale che a*a^-1=e,

se a H e H e*a^-1 H a^-1 H.

Dimostro che H è chiuso rispetto all' operazione *,

"a,b H b=(b^-1)^-1 b^-1 H a*(b^-1)^-1 H a*b H.

N.B.:Un gruppo (monoide) (G,*) ha sempre due sottogruppi (sottomonoidi) chiamati impropri; Quello formato da G stesso e . Tutti gli altri sono chiamati propri

Classe laterale sx:G gruppo H G e a G, si dice classe laterale sinistra di H l'insieme aH=.

Classe laterale dx:G gruppo H Ge a G, Si dice classe laterale destra di H l'insieme Ha=.

LEMMA 24.1

Se G è un gruppo, e H G e g G allora H è equipotente a gH.

Dimostrazione: L'applicazione f:H->gH definita come f(h)=g*h "h H, è una biiezione.

LEMMA 18.1

Sia G gruppo e H sottogruppo di G. L' insieme delle classi laterali sinistre di G modulo H è una partizione di G. (F= è una partizione di G).

Dimostrazione:

Dimostro che "g G gH : g=g*1_H gH g gH.

Dimostro che _{a G} aH=G: "a G a*1_H aH G _{a G} aH e _{a G} aH G, perché è l' unione di sottoinsiemi di G.

Dimostro che "a,b G con aH bH allora aH bH= . Se così non fosse allora esisterebbe c tale che:

c aH h₁ H t.c. a*h₁=c

c bH h₂ H t.c. b*h₂=c

a=b*h₁^-1*h₂ a*h=b*(h₁^-1*h₂*h) bH "a G a*h bH aH bH

similmente si prova bH aH quindi aH=bH assurdo.

Indice: Sia l' insieme di tutte le classi laterali di G modulo H. Se tale insieme è finito, allora la sua cardinalità si chiama indice di H in G e la si denota come [G:H].

Teorema

Sia G un gruppo e H sottogruppo di G, allora |H|=|aH|=|Ha|

Dimostrazione:

Sia a G definisco f:H->aH come f(a)=a*h "h H. Dimostro che f è biiettiva.

Iniettività) ??"h₁,h₂ H se ho f(h₁)=f(h₂) allora h₁=h₂??. Se f(h₁)=f(h₂) siccome a G allora esiste a^-1 G tale che a^-1*a*h₁=a^-1*a*h₂ 1_G*h₁=1_G*h₂ h₁=h₂.

Suriettività) ??"g aH esiste h H tale che f(h)=g??. Se g aH esiste h H tale che a*h=g per definizione di classe laterale sinistra di G mod H a*h=f(h)=g, questo "g aH.

La f così definita è biiettiva.

Teorema di Lagrange

Sia G gruppo e H sottogruppo, |G|=n, |H|=m allora m|n e più precisamente n=m*i dove i=|G:H|. (ovvero l'ordine di ogni sottogruppo finito di G divide l' ordine di G).

Conseguenze:

• Se n è primo G non ha sottogruppi propri
• G è ciclico se esiste g G tale che G=<g> (Non capisco cosa c'entri lagrange???).

Dimostrazione:

Sfruttando il teorema precedente, si ha che |H|=|aH|=|Ha|=m, allora n = |G| = | _k=1,.i(a_kH)| = =S_k=1,.i|a_kH| = S_k=1,.i m = i*m. (Il ragionamento cmq è che l'insieme , avevamo visto che era una partizione di G, quindi G si poteva dividere in [G:H] classi laterali, ognuna di |H| elementi.Quindi |G|=[G:H]*|H|.)

Sottogruppo normale: Si dice che H è sottogruppo normale di G se "a G si ha aH=Ha. Si indica Hv G.

Teorema

Sia G gruppo e H G sottogruppo. Allora

a)  H è sottogruppo normale

b)  "a G, "h H ho che a*h*a^-1 H.

Dimostrazione:

a b) "a G aH=Ha. g aH g Ha g=a*h e g=h'*a a*h=h'*a a*h*a^-1=h'*1_G=h' H (questo per qualsiasi h, perché prendo un g qualsiasi).

b a) Devo dimostrare che "a G aH=Ha. Allora dimostro che "a G aH Ha e Ha aH.

??aH Ha se "x aH x Ha??; x aH x=a*h e a*h*a^-1 H e a*h*a^-1=h' (a*h)*a^-1=h' a*h=h'*a Ha. ("x aH).

Simile alla precedente (??Ha aH se "x Ha x aH??).

Relazione d'equivalenza compatibile: Data una relazione di equivalenza su un gruppo (G,*), si dice che è compatibile con l' operazione * se "a,b,c,d G si ha a b e c d a*c b*d.

Si può dimostrare che:

in aH con la relazione a b (se a è nella stessa classe laterale di b) sse b^-1*a H.

in Ha con la relazione a b (se a è nella stessa classe laterale di b) sse a*b^-1 H.

Teorema

(a) Sia (G,*) un gruppo, e una relazione di equivalenza compatibile con *, allora [1_G] è un sottogruppo normale di G. (b) Viceversa se N è un sottogruppo normale di G e è definita per a,b G tale che a b se a^-1*b N, allora è una relazione di equivalenza su G compatibile con * e [1_G] =N.

Dimostrazione:

a)  Dobbiamo provare che [1_G] è un sottogruppo:

[1_G] perché 1_G [1_G]

Se [1_G] = allora [1_G] è un sottogruppo normale.

Altrimenti siano a,b [1_G] avrei che a 1_G e b 1_G, 1_G b a b. So che b^-1 b^-1, quindi  a*b^-1 b*b^-1 a*b^-1 1_G a*b^-1 [1_G] [1_G] è un sottogruppo.

Adesso provo che è normale.

"g G g g e prendo h [1_G] h 1_G g*h g*1_G=g e siccome g^-1 g^-1

g*h*g^-1 g*g^-1=1_G [1_G]

"g G g*h*g^-1 [1_G] [1_G] è normale.

b)  Presi a,b,c,d G con a b e c d:

a b b=a*h (b sta nella stessa classe laterale di a) con h N

c d d=c*h' con h' N

b*d=a*h*c*h'=a*(h*c)*h', che siccome N è normale allora h*c=c*h'' per qualche h''.

b*d=a*c*h''*h' h''*h' N allora poniamo h''*h'=h

b*d=a*c*h b*d (a*c)N a*c b*d.

E inoltre [1_G] ==N.

Nucleo e immagine dell' applicazione: Siano (G,°) e (G',*) due gruppi, e f un' applicazione   f:G->G'. Si chiama nucleo (ker) di f l' insieme . Si chiama invece immagine (im) di f l' insieme .

Omomorfismo: Si dice che f applicazione con f:G->G' con (G,°) e (G',*) due gruppi, è un omomorfismo se "g,g' G f(g ° g')=f(g)*f(g').

Isomorfismo: è un omomorfismo biunivoco.

Endomorfismo: è un omomorfismo f tale che f:G->G.

Automorfismo: è un endomorfismo biunivoco.

Teorema

Siano (G,°) e (G',*) gruppi e f:G->G' un omomorfismo. Allora:

a)  f(1_G)=1_G'. (il nucleo di un omomorfismo non è mai vuoto),

b)  f(a^-1)=(f(a))^-1.

Dimostrazione:

a)  f(1_G)=f(1_G°1_G)=f(1_G)*f(1_G) f(1_G) G' quindi (f(1_G))^-1 G' allora moltiplicando membro a membro ho che f(1_G)* (f(1_G))^-1= f(1_G)*f(1_G)* (f(1_G))^-1 1_G'=f(1_G)*1_G'.=f(1_G).

b)  1_G'=f(1_G)=f(a°a^-1)=f(a)*f(a^-1) f(a^-1) è l' inversa di f(a) quindi (f(a))^-1=f(a^-1).

Teorema

Siano (G,°) e (G',*) gruppi e f:G->G' un omomorfismo. Allora ker(f) è un sottogruppo normale di G.

Dimostrazione:

ker(f) sottogruppo) ??"a,b ker(f) a°b^-1 ker(f)??. a,b ker(f) quindi f(a)=f(b)=1_G'. E' vero anche che f(b^-1)=(f(b))^-1=(1_G')^-1=1_G'. Ma allora f(a°b^-1)=f(a)*f(b^-1)=1_G'*1_G'=1_G' a°b^-1 ker(f).

ker(f) sottogruppo normale) ??"g G "h ker(f) g°h°g^-1 ker(f)??. f(g°h°g^-1)=f(g)*f(h)*f(g^-1)= =f(g)*1_G'*f(g^-1)= f(g)*(f(g))^-1=1_G' g°h°g^-1 ker(f).

Teorema

Siano (G,°) e (G',*) due gruppi, f omomorfismo f:G->G'. Allora le due affermazioni sono equivalenti:

a)  ker(f)=.

b)  f è iniettiva.

Dimostrazione:

a)  "a,b G con f(a)=f(b) a=b??. Se f(a)=f(b), allora esiste (f(b))^-1 G' t.c. f(a)*(f(b))^-1= =f(b)*(f(b))^-1 f(a)*f(b^-1)=1_G'. f(a°b^-1)=1_G'. a°b^-1 ker(f)=1_G a=b.

b)  Se esistesse g ker(f) con g 1_G allora avremo per definizione di ker(f) f(1_G)=1_G' e f(g)=1_G' , che è assurdo perché f è iniettiva.

Teorema fondamentale di omomorfismo tra gruppi

Siano (G,°) e (G',*) gruppi e f:G->G' un omomorfismo, data la proiezione canonica p:G->G/ker(f), esiste ed è unico un omomorfismo f' con f':G/ker(f)->G' tale che f=f' p

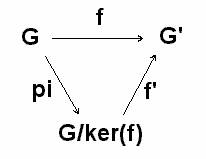
inoltre:

a)  f è iniettiva,

b)  f è un isomorfismo sse f è suriettiva.

Dimostrazione: Devo solamente dimostrare che f' è un omomorfismo (il resto è già stato dimostrato in precedenza). ?? " aKer(f),bKer(f) G/ker(f) (che indichero rispettivamente [a] e [b]) f'([a]°[b])=f'([a])*f'([b]) ??.

Vedo che f'([a]°[b])=f'([a°b]) per definizione di prodotto delle classi, ma f'([a°b])=f'(p(a°b)) perché p(a°b)=[a°b], e f'(p(a°b))=f' p(a°b)=f(a°b)=f(a)*f(b) (f è omomorfismo) e f(a)=f' p(a) e f(b)=f' p(b), quindi f'([a]°[b])=f'([a])*f'([b]).

PROPOSIZIONE 25.4

Sia f:G->G' un omomorfismo di gruppi. Allora:

a)  Se H G, f(H) G'

b)  Se H' G', f^-1(H') G

c)  Se H G, f^-1(f(H))=Hker(f)=

d)  Se H' G', alloraf(f^-1(H'))=H' f(G).

Dimostrazione:

a)  Dato che f(1_G)=1_G', allora f(H) . Dati f(a),f(b) f(H) ho che a,b H, ma f(a)*(f(b))^-1 = =f(a)*f(b^-1) = f(a°b^-1) f(H). Queste due cose dimostrano che f(H) G'.

b)  Dato che f(1_G)=1_G' allora f^-1(1_G')=1_G f^-1(H') . Dati a,b f^-1(H) , f(a),f(b) H' ma

f(a°b^-1)=f(a)*f(b^-1)=f(a)*(f(b))^-1 H' a°b^-1 f^-1(H'). Queste due cose dimostrano che f^-1(H') G.

c)  Sia x f^-1(f(H)), allora per qualche h H si ha f(x)=f(h). f(h^-1°x)=f(h^-1)*f(x)=(f(h))^-1*f(h)= =1_G'. Quindi h^-1°x ker(f) e h^-1°x=k per qualche k ker(f). Moltiplicando a sinistra per h si ha x=h°k e x Hker(f).

Viceversa se x Hker(f), allora x=h°k per opportuni elementi h H e k ker(f). Ne segue che f(x)=f(h°k)=f(h)*1_G' quindi x=f^-1(f(h)).

d)  "b f(f^-1(H')), si ha che b=f(a) con a f^-1(H'), quindi b=f(a) H'. Siccome a f^-1(H') G, allora b=f(a) f(G). Qundi b H f(G). (f(f^-1(H')) H' f(G)).

"b H' f(G), si ha che b H' e b f(G). b=f(a) per qualche a G. Essendo f(a)=b H' si deve avere a f^-1(H'), quindi b f(f^-1(H')). (f(f^-1(H')) H' f(G)).

(f(f^-1(H')) H' f(G), f(f^-1(H')) H' f(G) f(f^-1(H'))=H' f(G) ).

Teorema di corrispondenza per gruppi

Siano (G,°) e (G',*) gruppi e f:G->G' un omomorfismo. Sia S= S'=. F:S->S' con F(H)=f(H) è biunivoca. Inoltre se H è normale allora f(H) è normale e viceversa.

Dimostrazione:

Iniettività: ?? "H₁,H₂ S F(H₁)=F(H₂) H₁=H₂ ??

F(H₁)=F(H₂) f^-1(f(H₁))=f^-1(f(H₂)),

f^-1(f(H₁))=H₁ker(f), f^-1(f(H₂))=H₂ker(f) H₁=H₂.

Suriettività: ?? " H' S' esiste H S tale che F(H)=H'.??

H' G' f^-1(H')=H G (La controimmagine di un sottogruppo è un sottogruppo)

1_G' H' ker(f)=f^-1(1_G') H.

H normale H' normale)

H è normale, quindi "g G e h H avrò che g°h°g^-1 H.

??f(H) è normale, ovvero "g' Im(f) "h' f(H) g'*h'*g'^-1 f(H)??

"g' Im(f) esiste g G tale che g'=f(g) (quindi anche g'^-1=f(g^-1)),

"h' f(H) esiste h H tale che h'=f(h).

Se esiste h'' H tale che g'*h'*g'^-1=f(h'') allora g'*h'*g'^-1 f(H)

g'*h'*g'^-1=f(g)*f(h)*f(g^-1)=f(g°h°g^-1) pongo h''= g°h°g^-1 quindi g'*h'*g'^-1=f(h'').

Gruppo ciclico: Dato G gruppo, e dato X G, l' insieme intersezione di tutti i sottogruppi di G che contengono X si dice sottogruppo di G generato da X e si denota come <X>. Ad esempio, dato che il più piccolo sottogruppo di G è allora <>=. Se X= (ha un solo elemento), allora si scrive solamente <a> al posto di <> e tale sottogruppo è detto il sottogruppo ciclico di G generato da a.Un gruppo G si dice ciclico se esiste un elemento a G tale che G=<a>.

Dimostrazione: ??Il gruppo generato da <X> coincide con l' intersezione di tutti i sottogruppi che contengono X??

Sia G_S un sottogruppo di G "s N, dimostro che _{s N} G_s è un sottogruppo di G.

1_G G_s "s N 1_{G s N} G_s. _{s N} G_s

Se x,y _{s N} G_s allora x,y G_s "s N

Siccome G_s sottogruppo, ne segue che x*y^-1 G_s "s N e che x*y^-1 _{s N} G_s.

Osservazione: Se g è un elemento di un gruppo G, il sottogruppo ciclico di G generato da g è l' insieme delle potenze di g a esponente intero, cioè <g>=.

Permutazione Dato X_n= per n N* fissato insieme una permutazione di X_n è una applicazione biiettiva f:X_n->X_n.

S_n L' insieme di tutte le permutazioni su X_n, e l' operazione di composizione delle funzioni ° è un gruppo chiamato S_n oppure gruppo simmetrico su n oggetti.

La cardinalità di S_n è n!=(n)*(n-1)*.*1.

Ciclo di lunghezza d (d n) E' una permutazione f con le seguenti proprietà, esistono d elementi distinti a₁,.,a_d X_n, tali che "e X_n se e=a_i con i=1,.,d-1 f(e)=a_i+1, se e =a_d f(e)=a₁ e se e a_i con i=1,.,d allora f(e)=e.

Teorema di Caley

Sia (G,*) gruppo allora esiste G' sottogruppo di S_g tale che G G' (G è isomorfo a G').

(S_g si dice gruppo simmetrico o gruppo delle permutazioni, ovvero è il gruppo delle applicazioni biunivoche da G in G S_G=.)

Dimostrazione:

Se trovo una applicazione F con F:G->G omomorfismo e iniettiva, allora G' sottogruppo corrisponde ad Im(f) Sg.

Definisco F(a)=f_a:G->G t.c. "a G "x G ho f_a(x)=a*x.

Dimostro che f_a:G->G è biunivoca. E' iniettiva perché "x,y G con y x f_a(x)=a*x a*y=f_a(y). E' suriettiva perché "y G esiste x G tale che f_a(x)=y ovvero x=a^-1*y. Quindi f_a è biiettiva.

Adesso provo che F così definita è un omomorfismo. (??F(a*b)=F(a) F(b)??)

F(a*b)=f_ab:G->G

f_ab(x)=a*b*x "x G.

F(a) F(b)=(f_a f_b):G->G

(f_a f_b)(x)=f_a(f_b(x))=f_a(b*x)=a*b*x F(a*b)=F(a) F(b).

Adesso provo che F è iniettiva. Siccome F è un omomorfismo, basta dimostrare che ker(F)=

"x G f_1G(x)=x f_1G=i."a G con a 1_G f_a(x) i quindi ker(F)= F è iniettiva.

Ma allora G'=Im(F) S_G e G G'.

Anello: Un anello (A,+,*) è un insieme R dotato di due operazioni + e * soddisfacenti le seguenti condizioni:

a)  (R,+) è un gruppo abeliano

b)  (R,*) è un semigruppo

c)  distributività: "a,b,c R si ha (a+b)*c=a*c+b*c e c*(a+b)=c*a+c*b.

Un anello si dice commutativo se a*b=b*a "a,b R.

Se il semigruppo (R,*) ha un' identita e_r 0 (identità additiva), si dice che l'anello è un anello con unità (e_r si dice identità dell' anello).

Lemma 26.1

Sia R un anello e siano a,b R. Allora:

0*a=a*0=0 e (-a)*b=a*(-b)=-(a*b).

Dato che ogni anello è un gruppo abeliano rispetto all'addizione ed un semigruppo rispetto alla moltiplicazione, "a R è possibile definire il multiplo n-esimo n*a "n N e la potenza n-esima aⁿ "n N⁺.

Dimostrazione:

??0*a=0??

0*a=(0+0)*a=0*a+0*a siccome 0*a R allora esiste -(0*a) opposto.

0*a-0*a=0*a+0*a-0*a 0=0*a. si procede identicamente per a*0.

??(-a)*(b)=-(a*b)??

a*b+(-a)*b=(a+(-a))*b=0*b=0 a*b opposto di (-a)*b -(a*b)=(-a)*b. si procede identicamente per a*(-b).

Dominio di integrità: Anello commutativo con identità privo di divisori dello 0. Quindi un anello commutativo con identità è un dominio sse "a,b R si ha che a*b=0 a=0 e/o b=0.

Corpo: Un' anello (A,+,*) tale che (A-,*) è un gruppo.

Campo: Un' anello (A,+,*) tale che (A-,*) è un gruppo commutativo. Un campo è un anello commutativo con identità in cui ogni elemento non nullo è invertibile.

Teorema

Ogni campo è un dominio di integrità.

Dimostrazione: Sia R campo. Se R non è dominio di integrità, allora a*b=0 con a,b 0. Siccome R è un campo l' inverso di a è a^-1 e quindi b=1*b=a^-1*a*b=a^-1*0=0 assurdo.

Ideale: I A si chiama ideale se I , (I,+) è un sottogruppo e "x A "y I si ha x*y I e y*x I.

Omomorfismo tra anelli: Siano (A,+,*) e (A',+',*') due anelli e f:A->A' un' applicazione. F è un omomorfismo se f(a+b)=f(a)+'f(b) e f(a*b)=f(a)*'f(b) e f(1_A)=1_A' deve sempre essere vera.

(K[x],+,*) si dice l' anello dei polinomi, è un anello commutativo con identità dove lo 0 =(0,0,.,0), l'opposto di (a₀,a₁,.,a_n) è (-a₀,-a₁,.,-a_n), l' identità è 1=(1,0,.,0).

Teorema

Siano f,g K[x], g 0. Allora esistono e sono unici p,r K[x] tali che f=p*g+r con grad r<grad g.

(dimostrazione da fare?).