Teorema (Primo teorema di De l'Hospital)

matematica

Teorema

(Primo teorema di De l'Hospital)

Sia  un intorno di  , e siano f(x) e g(x) due funzioni definite e derivabili su tutto

(non è necessario fare 636d37g alcuna ipotesi sul comportamento delle due funzioni IN c, dove, addirittura, l'una o l'altra o entrambe le funzioni potrebbero persino non essere definite).

Sia inoltre

cosicché il calcolo del limite

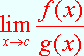
si presenti come forma di indecisione .

Supponiamo infine che sia

su tutto .

Bene!

il teorema dice che, sotto le ipotesi di cui sopra, se esiste il

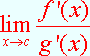
allora esiste pure il

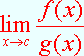
e coincide col precedente, ossia risulta

D

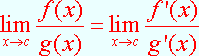
Il "secondo teorema di de l'Hospital"

Un enunciato analogo al precedente

vale se il limite del rapporto f/g

si presenta sotto la forma di indecisione  [  ]

• Esempio 4:

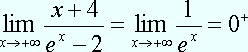
Quando si cita il "Teorema di De l'Hospital" ci si vuole di norma riferire indifferentemente all'uno o all'altro dei due teoremi che abbiamo presentato, o, se si preferisce, all'unico enunciato che si otterrebbe riunendoli.