I NUMERI DI FIBONACCI

Alla fine del primo mese:

Numero totale di coppie nella gabbia: C₁ = 1 coppia

Alla fine del secondo mese:

C₁ ha generato la sua prima coppia di cuccioli. Chiamiamola C_2.

Numero totale di coppie nella gabbia: C₁ + C₂ = 2 coppie

Alla fine del terzo mese:

C₁ ha prodotto una nuova coppia di cuccioli. Chiamiamola C₃.

C₂ non ha ancora dato vita a cuccioli in quanto è solo da un mese nella gabbia

Numero totale di coppie nella gabbia: C₁ + C₂ + C₃ = 3 coppie

Alla fine del quarto mese:

C₁ ha prodotto una nuova coppia di cuccioli. Chiamiamola C_4.

C₂ ha prodotto la sua prima coppia di cuccioli. Chiamiamola C₅.

C₃ non ha ancora dato vita a cuccioli in quanto è solo da un mese nella gabbia

Numero totale di coppie nelle gabbia: C₁ + C₂ + C₃ + C₄ + C₅ = 5 coppie

Alla fine dl quinto mese:

C₁ ha prodotto una nuova coppia di cuccioli. Chiamiamola C_6.

C₁ ha prodotto una nuova coppia di cuccioli. Chiamiamola C₇

C₃ ha prodotto la sua prima coppia di cuccioli. Chiamiamola C₈

C₄ e C₅  non ha ancora dato vita a cuccioli in quanto sono solo da un mese nella gabbia

Numero totale di coppie nella gabbia: C₁ + C₂ + C₃ + C₄ + C₅ + C₆ + C₇ + C₈ = 8 coppie

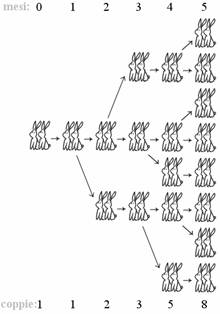Il resto della soluzione è simile a quanto dimostrato finora.

Dopo quanto tempo? Quante coppie nella gabbia?

Inizio 1 coppia

1 mese  1 coppia

2 mesi   2 coppie

3 mesi   3 coppie

4 mesi   5 coppie

5 mesi   8 coppie

6 mesi   13 coppie

7 mesi   21 coppie

8 mesi   34 coppie

9 mesi   55 coppie

10 mesi 89 coppie

11 mesi 144 coppie

12 mesi 233 coppie

Quindi la risposta all'enigma di Fibonacci è che dopo 12 mesi nella gabbia ci saranno 233 coppie. La soluzione è di per sé poco interessante. Sono invece estremamente curiose le tipologie di schemi che essa cela. Lo schema estrapolato mostra che ogni numero della sequenza è la somma  dei due numeri precedenti. Questa è una serie infinita indicata dai tre punti alla fine.

1,1,2,3,5,8,13,21,34, 55, 89, 144, 233, 377, 610, 987,.

Il numero di schemi che possono essere individuati nella sequenza di Fibonacci è a dir poco sbalorditivo. Tutto ciò da corpo alla credenza pitagorica secondo la quale i numeri, dopo tutto, potrebbero essere il linguaggio segreto dell'universo.

Analizziamo alcuni degli schemi celati nella sequenza di Fibonacci.

Il rapporto fra due numeri consecutivi della sequenza di Fibonacci tende al numero decimale illimitato 0,6180339.

Es.  = 0,615384 = 0,6180344

Questo rapporto risulta essere la Sezione aurea che si indica anche con la lettera greca phi.

La sequenza che si ottiene elencando le differenze tra due numeri di Fibonacci consecutivi dà vita alla sequenza di partenza

Es.  2 1 = 1 3 5 8 13

La somma dei quadrati di due numeri di Fibonacci consecutivi è un numero di Fibonacci.

Es. 2²+3² = 13    3²+5² = 34 5²+8² = 89 8²+13² = 233 13²+21² = 610 21²+34² = 1597

Il terzo numero è 2, e ogni terzo numero dopo il 2 è un multiplo di 2. Il quarto numero è 3, e ogni quarto numero dopo il 3 è un multiplo di 3. Il quinto numero è 5, e ogni quinto numero dopo il 5 è un multiplo di 5. E così via. In generale, se l'n-esimo numero della sequenza è x, allora ogni n-esimo numero dopo x risulta essere multiplo di x.

Nel triangolo di Pascal, uno dei fondatori della moderna teoria della probabilità, un numero in una certa riga è la somma dei due numeri appena sopra di lui nel triangolo.

Es. Il primo 3 nella quarta riga dall'alto corrisponde alla somma dei due numeri che gli stanno sopra.

Gli schemi numerici apparentemente infiniti della sequenza di Fibonacci, oltre a tutti quelli che i matematici continuano a trovare al suo interno, coprono tutto ciò che si può dire di questa serie assolutamente notevole. Per qualche strano motivo, i numeri di Fibonacci si ripresentano in natura e, come il numero phi, potrebbe costituire un'importante chiave per capire come funziona l'universo.

Melissa Lupone