CARATTERISTICHE DELLO STIMATORE MEDIA CAMPIONARIA

matematica

CARATTERISTICHE DELLO STIMATORE MEDIA CAMPIONARIA.

I problemi della statistica consistono nel valutare alcune caratteristiche della popolazione qua 818i88i li:

Media campionaria;

Varianza;

Coefficiente di correlazione;

Ecc..

Controlliamo se la stima per m sia corretta o meno.

Si tratta di calcolare

Innanzitutto calcoliamo .

Per definizione = in quanto in precedenza si è visto che assume tutti i valori previsti dalla popolazione con probabilità .

Analogamente e .

Consegue che:

Cioè la media campionaria è una stima non distorta per la media della popolazione m

DIMOSTRARE CHE LA MEDIA CAMPIONARIA E' UNO STIMATORE

CONSISTENTE PER LA MEDIA m DELLA POPOLAZIONE.

Si dimostra nello stesso modo della 13

SIA LO STIMATORE MEDIA CAMPIONARIA, DIMOSTRARE A COSA E'

UGUALE Var().

La: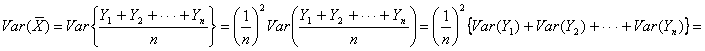

E' interessante notare che la varianza della stima è inversamente proporzionale alla numerosità del campione.

 

DIMOSTRARE CHE LA VARIANZA E' UNO STIMATORE DISTORTO PER LA VARIANZA s2 DELLA POPOLAZIONE.

Si dimostra come la domanda precedente.