I LIMITI - Intervallo limitato

Intervallo illimitato:

-superiormente ]a;+ [ o [a;+ [

Dato 1 numero a qualsiasi l’insieme di tutti i numeri reali maggiori di a è detto intervallo illimitato

Superiormente di estremo inferiore a.

-inferiormente ]-;a[ o ]- ;a]

Analogamente sarà l’insieme di tutti i numeri reali minori di a.

Intorno di un punto:

Definiamo intorno di un punto c, un qualsiasi intervallo limitato aperto che abbia c come punto interno ( o a cui c appartenga).

Definiamo intorno sinistro e destro di c un qualsiasi intervallo limitato aperto che abbia c rispettivamente estremo superiore/inferiore di quell’intervallo.

1 caso di limite:

Si dice che per x tendente a c, la funzione f(x) ha per limite il numero l (sottointeso reale) se scelto un numero arbitrario piccolo a piacere positivo , è possibile determinare in corrispondenza di esso un intorno completo del punto c tale che per ogni x appartenente a tale intorno, escluso al +c i corrispondenti valori di f(x) differiscono in modulo da l- di , cioè valga la disequazione |f(x) – l|<

o ciò che è lo stesso l - < f(x) < l +

Esempio:

lim   

; ; ; ;

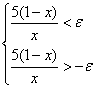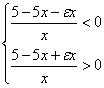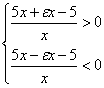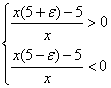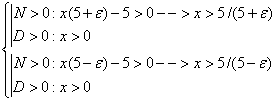
0 5/(5+) 1 5/(5-)

Il limite non è verificato per x

Ma per x

2 caso di limite:

Si dice che per x tendente a c, la funzione f (x) ha per limite l’infinito, se scelto un numero positivo M grande a piacere è possibile, determinare in corrispondenza di esso un intorno completo del punto c, per ogni x del

quale,escluso c, i corrispondenti valori di f(x) sono in valore assoluto maggiori di M, cioè valga la disequazione | f(x) | > M

lim f (x) = + |f(x)|> M f(x) > M (+)

x c  f(x) <- M (-)

Esempio:

lim

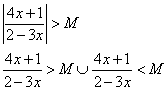
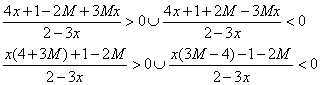
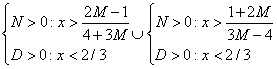
chi è maggiore?

- Fra e :

-11M;11M è maggiore

- Fra e :

è maggiore

- Fra e :

è maggiore

2M-1/(3M+4) 2/3 2/3 2M+1/(3M-4)

2M-1/(3M+4) 2/3 2M+1/(3M-4)

Il limite è verificato!

3 caso di limite:

Si dice che per x tendente ad infinito la funzione f(x) ha per limite il numero reale l, se scelto un numero arbitrario piccolo a piacere , è possibile determinare in corrispondenza di esso un numero positivo N, tale che per tutte le x che in modulo siano maggiori di N i corrispondenti valori di f(x) differiscono in modulo da – di , cioè valga la disequazione |f(x) – l | <
lim f(x) = l |x| > N x >N : lim f(x) = l

x x

x <- N : lim f(x) =l

xà-

4 caso di limite:

Si dice che per x tendente ad infinito la funzione f(x) ha per limite infinito, se scelto un valore arbitrario grande a piacere positivo M; è possibile determinare in corrispondenza di esso un numero reale N, tale che per ogni x che in modulo sono maggiori di N i corrispondenti valori di f(x) siano in modulo maggiori di M, ossia valga la disequazione |f(x) |> M

lim f(x) =

x

TEOREMA DELL’UNICITA’ DEL LIMTE:

Se una funzione y = f(x) per x tendente a c (finito/infinito) ammette un dato limite (finito/infinito), questo limite è UNICO.

TEOREMA DEL CONFRONTO:

Siano f, g ,h tre funzioni definite in un intorno I di x, escluso al più il punto x e tali che per ogni x I risulti:

Se lim f(x) = lim h(x) = l allora risulterà : lim g(x) = l

x x x x   x x

TEOREMA DELLA PERMANENZA DEL SEGNO:

Se lim f(x) = l

x c

esiste un intorno I (c) di c, privato al più del punto c, in cui la funzione assume lo stesso segno di l.

Viceversa se esiste un intorno I (c) di c, privato al più del punto c, in cui risulta f(x) > 0 (f(x) < 0), e se esiste il lim f(x) = l si avrà l

x c

OPERAZIONI SUI LIMITI:

TEOREMA: il limite di una somma di funzioni è uguale alla somma dei limiti delle funzioni, se questi sono finiti. Date cioè:   lim f(x) =l lim g(x) =l lim

x c x c   x c

TEOREMA: il limite di un prodotto di funzioni è uguale al prodotto dei limiti delle funzioni, se questi sono finiti. Date cioè:   lim f(x) = l lim g(x) = l lim

x c x c    x c

TEOREMA: lim kf(x) = kl

x c

TEOREMA:  lim

x c

TEOREMA: se l > 0 lim log

x c

TEOREMA: lim a

x c

TEOREMA: se lim f(x) = l >0 e lim g(x) = l si ha: lim