La formula risolutiva delle equazioni di 3° grado

matematica

La formula risolutiva delle equazioni di 3° grado

Vogliamo risolvere l'equazione di 3° grado :

Ponendo riduciamo l'equazione data alla sua forma normale :

(1)

dove :

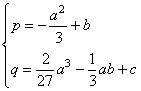
La formula è meno misteriosa di quanto possa sembrare.

Data un'equazione di grado n e primo coefficiente 1, , il coefficiente a di è l'opposto della somma delle radici. Poiché le radici so 131f55b no tre, a/3 è il baricentro delle radici. Il cambio delle coordinate sarà la nuova somma delle radici, che deve essere zero, perché il nuovo baricentro è l'origine.

Torniamo all'equazione (1). Supponiamo e . Cerchiamo le soluzioni ponendo :

dove u e v sono complessi. Elevando al cubo ambo i membri :

affinché questa equazione sia equivalente alla (1) deve essere :

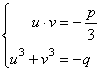(2)

eleviamo al cubo la prima equazione, ottenendo il sistema :

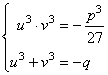(3)

I sistemi (2) e (3) non sono equivalenti. Quindi, risolto il sistema (3), occorre scartare quelle soluzioni che non sono valide per il sistema (2). Il sistema (3) è simmetrico e l'equazione in z associata è :

(4)

le cui soluzioni sono :

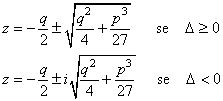
Consideriamo il caso . Si ha:

con:

da cui:

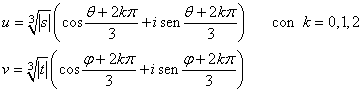
perciò :

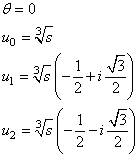
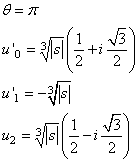
Se allora , e può scriversi :

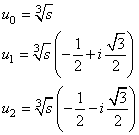
Posto ora :

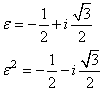
con e radici complesse dell'equazione , si ha :

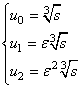
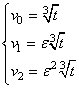
Bisogna ora scegliere le coppie in modo che :

E' subito visto che le coppie da considerare sono :

Pertanto:

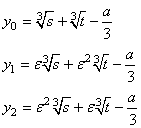
che costituiscono le formule di risoluzione dell'equazione di terzo grado quando il dell'equazione (4) è positivo (o nullo, caso in cui si ha una radice doppia). Il caso si risolve in maniera analoga, e viene lasciato come esercizio per il lettore.

7. Un'applicazione: correnti elettriche variabili nel tempo

Molte questioni fisiche che coinvolgono grandezze variabili periodicamente si prestano all'uso dei numeri complessi. In questo esempio, analizzeremo un semplice circuito in corrente alternata.

Ci interessa calcolare

la relazione fra le ampiezze e

il ritardo di fase della corrente rispetto alla f.e.m.

Analizziamo separatamente gli effetti della resistenza R e dell'induttanza L. Se il circuito presentasse solo una resistenza R si avrebbe una f.e.m. di ampiezza:

in concordanza di fase con la corrente I. Se invece il circuito presentasse dolo un'induttanza L, che agisce opponendosi alla variazione di intensità di corrente, si avrebbe una f.e.m. di ampiezza :

in quadratura di fase con la corrente. Ne segue che per produrre nel circuito la corrente I è necessario impiegare entrambe le f.e.m. appena scritte.

Z viene chiamata impedenza complessa del circuito, ed ha modulo :

e argomento :