|
|
| |
![]()
Campo di esistenza
per il campo di esistenza dobbiamo considerare tre casi:
Altrimenti, al di fuori di questi casi, il campo di esistenza e' tutto l'asse reale
Determinazione di alcuni tipi particolari di funzione
Veramente la determinazione del tipo di funzione (intera,
razionale, fratta,..) deve essere fatta all'inizio prima della determinazione
del campo di esistenza.
Qui consideriamo alcuni tipi di funzione che ci aiutano a costruire il loro
grafico e precisamente:
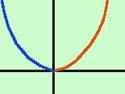 Per le funzioni pari bastera' costruire
solo meta' grafico poi farne il simmetrico rispetto all'asse delle y
(simmetria assiale). In pratica lo ribalto attorno all'asse y. In blu la
parte ribaltata.
Per le funzioni pari bastera' costruire
solo meta' grafico poi farne il simmetrico rispetto all'asse delle y
(simmetria assiale). In pratica lo ribalto attorno all'asse y. In blu la
parte ribaltata.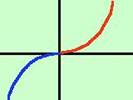 Per le funzioni dispari bastera'
costruire solo meta' grafico poi farne il simmetrico rispetto all'origine
(simmetria centrale) In pratica primo lo ribalto rispetto all'asse y ed il
risultato lo ribalto ancora attorno all'asse x, In blu la parte ribaltata
due volte
Per le funzioni dispari bastera'
costruire solo meta' grafico poi farne il simmetrico rispetto all'origine
(simmetria centrale) In pratica primo lo ribalto rispetto all'asse y ed il
risultato lo ribalto ancora attorno all'asse x, In blu la parte ribaltata
due volte 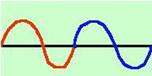 Per le funzioni periodiche basterà
costruire un periodo e poi ripeterlo su tutto l'asse reale. in blu il
periodo ripetuto una prima volta
Per le funzioni periodiche basterà
costruire un periodo e poi ripeterlo su tutto l'asse reale. in blu il
periodo ripetuto una prima volta Punti di intersezione con gli assi
Si tratta di calcolare le coordinate dei punti in cui la funzione incontra gli assi coordinati:per fare cio' occorre fare
Da notare che se in una funzione non trascendente y=f(x) manca il termine noto, allora la funzione passa per l'origine
Valori agli estremi del campo di esistenza
Quando il campo di esistenza e' diverso da tutto R meno qualche punto e vi sono
delle zone della retta reale in cui la funzione non e' definita e' bene andare
a controllare qual è il valore della funzione nei punti che separano queste
zone: attenzione però che devi fare il limite solo dalla parte dove la funzione
e' definita. (limite della funzione
dove qst è definita)
Positivita' e negativita'
Serve per individuare in quali parti del piano passera' il grafico della funzione
Si deve porre la funzione maggiore di zero e trovare per quali valori di x e' verificata: per tali valori il grafico sara' sopra l'asse delle ascisse mentre per valori diversi sara' sotto.
Determinare gli asintoti serve per veder come la funzione si comporta all'infinito.
Prima conviene calcolare gli asintoti verticali facendo
tendere la x verso i punti di discontinuita' della funzione; se il valore del
limite vale infinito esiste l'asintoto verticale ed allora conviene anche
calcolare il limite destro e sinistro nei punti
Si passa poi a determinare, se esistono, gli asintoti orizzontali od obliqui
facendo il limite della funzione per x tendente ad infinito
Calcolo della derivata prima
Si calcola la derivata prima per poter poi individuare la crescenza e la decrescenza della funzione ed anche i massimi ed i minimi
Crescenza e decrescenza della funzione
Fatta la derivata della funzione la si pone maggiore di zero: nell'intervallo dove la diseguaglianza e' verificata avremo che la funzione e' crescente mentre dove non e' verificata la funzione sara' decrescente
Determinazione dei massimi e minimi
Si usa il metodo della derivata seconda prima
dovrai calcolarla. (CALCOLARE DERIVATA SECONDA!!!)
Determinazione della concavita', convessita' e dei punti di flesso
Ponendo la derivata seconda maggiore di zero e risolvendo la disequazione avremo gli intervalli in cui la funzione rivolge la concavita' verso l'alto ed inoltre troveremo i punti dove cambia di concavita' (cioe' i punti di flesso)
Determinazione di altri eventuali punti
Per individuare dei punti ove non si sa di preciso come si comporti la funzione basta sostituire dei valori alla x e calcolare i valori corrispondenti per la y, otterremo cosi delle coordinate di punti per cui passa la funzione.
Grafico della funzione
Si tratta ora di impostare un grafico in cui mettere tutti i dati trovati sviluppando i vari punti e quindi unirli con una linea
L'unica cosa cui fare attenzione e' l'uso di una opportuna unita' di misura, che permetta di avere un grafico abbastanza ampio ma anche che permetta di vederne i particolari; anche qui devi decidere caso per caso
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026