|
|
| |
numeri complessi
 Numeri immaginari:
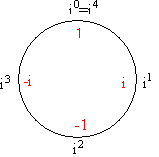
Numeri immaginari:
Definiamo i2 = -1
Si avrà: (- i)2 = -1; ( i)2 = -1
Nell'insieme dei numeri immaginari, esistono due numeri che elevati al quadrato danno -1
Si conviene che: ![]()
L'addizione e l 333i89d a sottrazione di numeri immaginari dà come risultato un numero immaginario
Il prodotto e il quoziente di due numeri immaginari sono numeri reali
Il quadrato di un numero immaginario è un numero reale negativo
Numeri
complessi 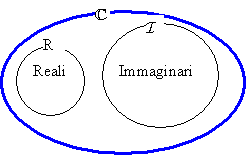
Siano a , b R
La somma di un numero reale e di un numero immaginario si dice numero complesso a + ib
Il numero a si dice parte reale del numero complesso, ib è la parte immaginaria e b è il coefficiente dell'immaginario
Due numeri complessi si dicono uguali quando hanno rispettivamente uguali le parti reali e i coefficienti dell'immaginario
Due numeri complessi che hanno la stessa parte reale ed opposti i coefficienti dell'immaginario si dicono complessi e coniugati
La somma di due o più numeri complessi si definisce come il numero complesso che ha per parte reale la somma delle parti reali degli addendi e per coefficiente della parte immaginaria la somma dei coefficienti della parti immaginarie.
Due numeri complessi si dicono opposti quando sono opposte sia la parte reale sia quella immaginaria.
Per differenza di due numeri complessi si intende la somma del primo con l'opposto del secondo
Si chiama reciproco del numero complesso c+di, diverso da zero, il numero complesso che moltiplicato per c+di dà 1, esso è 1/(c+di)
Per quoziente di due numeri complessi si intende il prodotto del primo per il reciproco del secondo
Per l'elevamento a potenza si applicano le consuete regole
Rappresentazione
geometrica dei numeri complessi: a + ib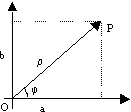
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025