 |  | |
|
| | |
|
| |
IL MOTO ARMONICO DELLA MOLLA
SCOPO DELL'ESPERIMENTO
Calcolare la costante elastica k di due molle con metodo statico, e verificare che l'allungamento dipende da k.
Calcolare la costante elastica di due molle con metodo dinamico, e verificare che il periodo dipende dalla massa.
Calcolare la costante elastica di
un sistema di molle collegate in serie verificando che č valida la formula: 
Disporre i punti ottenuti su un grafico e verificare che la curva algebrica ottenuta č una retta passante per l'origine degli assi.
APPARATO STRUMENTALE
PROCEDIMENTO
1a fase
Per calcolare la costante elastica delle due molle ci siamo serviti della formula che lega la forza F all'allungamento x della molla dopo che č stato attaccato un peso sotto di essa:
Č stata dapprima misurata la massa di ogni
pesetto servendoci della bilancia, poi utilizzando il metro abbiamo misurato
l'allungamento della molla ottenuto per ogni pesetto. Dopo aver disposto i dati
nella tabella riportata sotto, abbiamo calcolato il valore di m/
, e disposto i punti su un grafico.
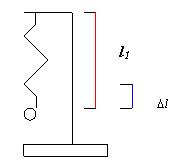
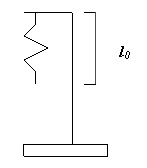Per ridurre al minimo gli inevitabili errori accidentali nel calcolo
dell'allungamento, č stata rilevata dapprima la lunghezza l0 della molla
in posizione di equilibrio (senza nessun pesetto) tenendo il metro fisso
sull'estremitā dell'asta, e poi tale misura č stata sottratta a quella ottenuta
dopo aver vincolato i diversi pesetti alla molla.
|
MOLLA 1 |
||
|
m(kg) |
Dl (m) |
m/Dl (m) |
|
m1=
|
|
|
|
m2=
|
|
|
|
m3=
|
|
|
|
m4=
|
|
|
|
m5=
|
|
|
|
m6=
|
|
|
|
MOLLA 2 |
||
|
m(kg) |
Dl (m) |
m/Dl (m) |
|
m1=
|
|
|
|
m2=
|
|
|
|
m3=
|
|
|
|
m4=
|
|
|
|
m5=
|
|
|
|
m6=
|
|
|
Moltiplicando la massa per l'accelerazione di gravitā, otteniamo la forza peso a cui č sottoposta la molla. Quindi, moltiplicando m/Dl per 9,8 otterremo proprio la costante k
P=mg quindi:
Dal momento in cui abbiamo ottenuto 6 misure diverse per ogni molla, č possibile calcolare il valore medio di tali misure, e i rispettivi errori assoluti ed errori relativi.
=> 
=> 
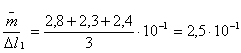
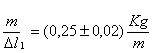
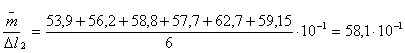
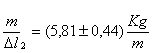
Gli errori sul calcolo di 
e 
incidono
rispettivamente del 7% e dell'8% sulle misure, ed essendo superiori al 5%, le
misure non sono molto accurate.
2a fase
Per calcolare k con metodo dinamico, abbiamo vincolato le diverse masse alle due molle, e abbiamo cronometrato il periodo di oscillazione. Per ridurre al minimo gli inevitabili errori di misura, abbiamo calcolato un Dt di 20 oscillazioni, e poi abbiamo ottenuto il periodo T dividendo tale tempo per 20.
Č stato misurato il periodo della molla 1, e del sistema formato dalla molla 1 e la molla 2, e i dati sn stati riportati nelle seguenti tabelle:
|
MOLLA 1 |
||
|
m(kg) |
Dt (s) |
T (s) |
|
m1=
|
|
|
|
m2=
|
|
|
|
m3=
|
|
|
|
m4=
|
|
|
|
m5=
|
|
|
|
m6=
|
|
|
|
MOLLA 1+MOLLA2 |
||
|
m(kg) |
Dt (s) |
T (s) |
|
m1=
|
|
|
|
m2=
|
|
|
|
m3=
|
|
|
|
m4=
|
|
|
|
m5=
|
|
|
|
m6=
|
|
|
In base ai dati ottenuti, č possibile calcolare k utilizzando la formula:
Elevando al quadrato primo e secondo membro, otteniamo:
Utilizzando la formula č possibile calcolare k1 e k12:
Ora calcoliamo il valore medio, l'errore assoluto, e l'errore relativo:
Gli errori
incidono del 9% sulla misura.
Anche questa volta calcoliamo il valore medio, l'errore assoluto, e l'errore relativo:
Gli errori
incidono dell'8% sulla misura.
3a Fase
Ora non ci resta che sostituire i dati ottenuti alla formula:
Quindi:
Notiamo che
si avvicina molto a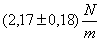 
Martino Giaquinto 4^ D
Liceo Scientifico C.Colombo
Marigliano (NA)
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025
