ESPERIENZA DI LABORATORIO N.4 - PENDOLO REVERSIBILE

Gli strumenti utilizzati nell'esperienza sono:

Pendolo composto costituito da due coltelli

Fotocellula elettronica

I FASE

Nella prima fase dell'esperienza la massa m₁ rimane alla distanza fissa di 21 cm dal coltello S_1, mentre si fa variare la distanza iniziale di m₂ dal coltello S₁ di 5 cm in più e 5 cm in meno. Si ottengono così tre punti sperimentali coincidenti con le distanze d₁ = 21 cm , d₂ = 26 cm, d₃ = 16 cm. Grazie al supporto della fotocellula elettrica si compiono 20 oscillazioni intorno ai due coltelli S₁ e S₂ per tutte e tre le distanze con angolo di partenza pari a 3°.

I valori ottenuti sono stati riportati nelle seguenti tabelle:

Con i valori ottenuti possiamo tracciare un grafico costituito da due rette:

la prima formata dalla media dei tempi di oscillazione di tutte e tre le distanze con centro di rotazione coincidente con coltello S₁

la seconda formata dalla media dei tempi di oscillazione delle tre distanze con centro di rotazione coincidente con il coltello S_2.

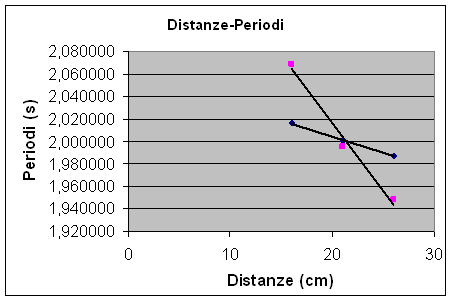
Il punto in cui le due rette si intersecano rappresenta una stima del punto di reversibilità del pendolo composto.

Dal grafico si evince che questo punto coincide con la distanza d_{1 =} 21 cm della massa m₂ dal coltello S₁.

II FASE

Nella seconda fase dell'esperienza si infittiscono le misure intorno al punto stimato nella prima fase, facendo variare m₂ di 1 cm dal coltello S₁, in modo da ottenere con maggiore precisione il punto di reversibilità, il quale può o meno coincidere con quello determinato precedentemente.

In questa fase per ogni punto sperimentale consideriamo 40 oscillazioni partendo sempre da un angolo di 3°. Iniziando da d₁ = 21 cm, consideriamo le distanze d₂ = 22 cm, d₃ = 23 cm, d₄ = 24 cm e d₅ = 20 cm, d₆ = 19 cm, d₇ = 18 cm.

Otteniamo i seguenti valori riportati in tabelle:

Una volta ottenuti tutti i periodi determiniamo la media, le deviazioni standard e le deviazioni standard della media.

Su un grafico si riportano la media dei periodi e le distanze della massa m₂ dal coltello S₁.

Quando si compie il best fit di una misura si tende a trascurare l'effetto dell'errore su x, quindi per verificare quale delle due variabile deve essere posta sull'asse delle x bisogna verificare la seguente disuguaglianza:

dove b è la pendenza della retta ottenuta dal grafico considerata con il suo valore assoluto, σ_max è il massimo valore della deviazione standard della media e Δy è l'errore sulla variabile posta sull'asse delle y.

Decidendo di considerare la media dei periodi come variabile indipendente e la distanza come variabile dipendente otteniamo il seguente grafico:

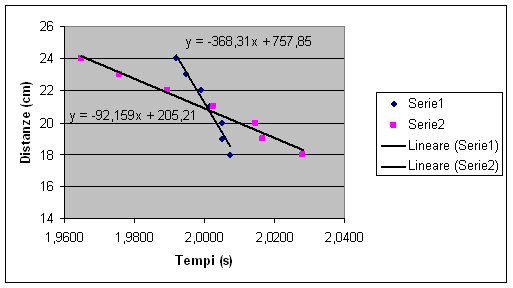
Determiniamo la regressione lineare per entrambe le rette:

Il primo elemento a sinistra della matrice delle regressioni lineare rappresenta la b cioè la pendenza delle due rette.

Conoscendo questo valore si può determinare  per entrambe le rette, e si ottiene:

• Prima retta: = 363,3 * 0,0001 = 0,04
• Seconda retta: = 92,2 * 0,0001 = 0,009

Ricordando che Δy = 0,1 cm è l'errore di sensibilità sulle distanze, dovuto allo strumento utilizzato, possiamo osservare che la disuguaglianza è verificata.

Quindi l'ipotesi assunta che la media dei periodi è la variabile indipendente e la distanza la variabile dipendente è giusta.

Poiché sull'asse delle ordinate abbiamo delle misure affette da errore di sensibilità si può semplicemente ricorrere ad un  fit non pesato per determinare le rette dei minimi quadrati.

III FASE

Nell'ultima fase dell'esperienza si vuol determinare il valore dell'accelerazione di gravità

Per prima cosa si nota che nel punto di reversibilità, cioè il punto in cui le due rette sono incidenti, c'è una dipendenza statistica dei parametri in quanto la stima di un parametro influenza la stima degli altri anche se i punti sperimentali sono statisticamente indipendenti.

Si determinano le covarianze per entrambe le rette con la seguente formula:

Dove k rappresenta l'incertezza statistica sulle y, uguale per tutti i punti sperimentali, ottenuto dalla matrice della regressione lineare.

• La covarianza per la prima retta è cov(a₁, b₁ ) = -2199,372141
• Per la seconda retta è cov(a₂, b₂ ) = -75,07874649

In seguito si determinano le coordinate del punto di intersezione P delle due rette dei minimi quadrati :

per la prima retta

per la seconda retta

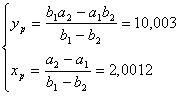
determiniamo la con la seguente formula:

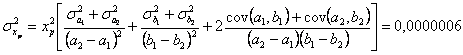
e infine la

Per l'accelerazione di gravità si deve usare la formula :

m/s²

Dove l = 0,9939 m  rappresenta la distanza tra i due coltelli S₁ e S₂.

L'errore su g si determina facendo la derivata della sua equazione rispetto a T ottenendo:

=

Quindi g = (9,797 ± 0,008) m/s²