|
|
| |
Cenni di Matematica Attuariale
2.1. Interesse e Future Value di Somme Versate
Affrontiamo il seguente problema : vogliamo conoscere il valore che una somma P investita oggi, avrà dopo un certo periodo di tempo ; cerchiamo cioè il "Valore Futuro" di P.
Prima si tutto, è necessario introdurre il concetto di interesse e di tasso d'interesse : l'imposizione di un onere finanziario per l'uso di denaro è una pratica che risale ai tempi più antichi della storia.
L'interesse è il compenso che si paga o si riscuote per il prestito di denaro.
Il concetto di interesse può essere esteso ai beni capitali, che si prendono in prestito dal loro proprietario, e che si ripagano attraverso i ricavi da essi generati. Questo guadagno economico che si ottiene dall'uso del denaro è ciò che dà alla moneta il suo valore nel tempo. Poiché i progetti di ingegneria richiedono l'investimento di denaro, è importante che, nella valutazione di questi progetti, il valore nel tempo della moneta impiegata sia adeguatamente preso in considerazione.
Il tasso d'interesse, o tasso di crescita del capitale, è il rapporto tra la redditività di un investimento e l'entità dell'investimento stesso.
Di solito questo tasso viene calcolato su base annuale e rappresenta il guadagno percentuale realizzato dal denaro impiegato dall'impresa.
Interesse semplice
In questo caso l'interesse maturato non viene capitalizzato e si valuta attraverso l'espressione :
I=(P i t )
dove:
I= Interesse maturato
P= somma versata
i= tasso d'interesse
t= periodo di tempo
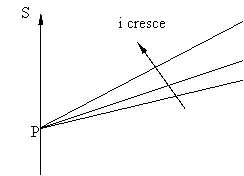
Quindi il valore di P dopo t anni sarà :
S=P (1 + i t)
S=Somma dopo t anni
P= Somma iniziale versata
t
Interesse composto
Gli interessi maturati negli anni vengono capitalizzati, cioè l'interesse maturato viene reinvestito andando ad incrementare anno per anno la somma versata: si ottiene quindi una serie geometrica.
Si noti con il semplice prospetto sotto riportato la differenza tra interesse semplice e composto.
Anno 0 i=10% anno 1 anno 2 anno 3
![]()
![]()
![]()
Interesse composto: 100 110 121 133,1
Interesse semplice: 100 110 120 130
S
![]()
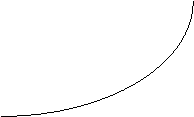
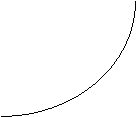
i cresce


P t
![]()
Quindi S può valutata attraverso l'espressione:
![]() Relazione Esponenziale [ 1 ]
Relazione Esponenziale [ 1 ]
La formula [1] vale se il calcolo dell'interesse maturato viene effettuato alla fine di ogni anno; inoltre t deve essere espresso in anni .
Se invece gli interessi vengono pagati più di una volta durante l'anno (per esempio ogni trimestre) si usa la seguente formula (2):
![]()
dove :
n= n° di anni totali
m= n° di volte in cui si capitalizzano gli interessi in un anno
(Es: tasso di interesse trimestrale, m=4; bimestrale, m=6).
i= tasso di interesse annuo
2.1.3. Future Value di un'annualità A versata alla fine di ogni anno
![]()
![]()
![]()
![]()
A A A A
3 ..... n
![]()
|
t |
Supponiamo che alla fine di ogni anno venga versata sul C.C. una somma costante A (per esempio un'annualità A di 1 Ml ); il tasso d'interesse annuo pagato dalla banca sia i (p.es. i=10%).
Vogliamo conoscere il valore della somma accumulata dopo N anni. Il suo valore futuro si ottiene dall'espressione:
FV = 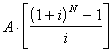 dove A
= annualità versata
dove A
= annualità versata
E' importante ricordare che tale formula vale quando i versamenti sono fatti a fine anno (31 dicembre); inoltre si suppone che i = cost e A= cost negli anni.
Cerchiamo, attraverso un esempio, di evidenziare le differenze tra un versamento effettuato ad inizio anno oppure a fine anno.
Versamento Posticipato a Fine Anno
Usando l'espressione (3) con : i= 10% A=10 M£ N=5 FV = 61 M£
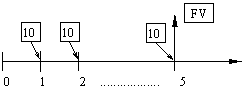
Versamento Anticipato ad Inizio Anno
61 M£
-10 M£
+10 * 1,15 M£
= 66,1 M£

Riprendiamo la formula [3]: se da questa esplicito A trovo la somma che devo versare ogni anno per avere alla fine degli n anni un capitale pari a FV.
A = FV / 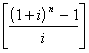
2.2. Valutazione del Present Value
Vediamo ora come determinare il Valore Presente di una somma che verrà incassata in un periodo futuro, nonché il Present Value di un'annualità costante A versata.
Valore Presente
Il calcolo del Present Value si effettua mediante la formula
PV =![]() [ 4 ]
[ 4 ]
dove: S= somma riferita al tempo t (S >PV)
i = tasso d'interesse
S
![]()
PV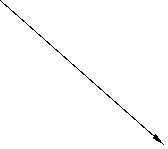



![]()
i cresce

2.2.2. Valore presente di un versamento annuale A
Per valutare il PV quando si versa ogni anno una somma A si utilizza l'espressione:
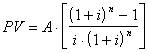 [
5 ]
[
5 ]
Esplicitando da tale relazione A trovo la rata che si deve pagare annualmente per coprire un mutuo di N anni.
Il fattore tra parentesi quadra per il quale viene moltiplicata l'annualità A è detto fattore di attualizzazione di una serie di pagamenti uguali.
Esempio: Contraggo un prestito dalla banca di 100M£ con i=10% per n=10 anni la rata che devo pagare annualmente è data dalla [ 5 ] in cui l'incognita è A:
A = 16,27 [M£/anno]
si noti che se i = 9% A = 15,58 [M£/anno]
i = 8% A= 14,90 [M£/anno]
risulta quindi evidente come A non vari linearmente con i.
Supponiamo di analizzare l'espressione [ 5 ] nel caso di numero di anni n grande, al limite:
![]()
Questa formula vale quindi quando siamo in presenza di versamenti perpetui: si ipotizza cioè che la somma A verrà versata con continuità all'infinito.
2.2.3. Il fattore della serie gradiente uniforme
In molti casi i pagamenti annuali non vengono fatti in serie di pagamenti uguali. Essi possono crescere o decrescere di una somma costante. Ad esempio, una serie di pagamenti uniformemente crescente è data da 100, 125 ,150 ,175 milioni di lire, pagati alla fine del primo, secondo, terzo, quarto anno.
In generale, una serie di pagamenti uniformemente crescente per n periodi d'interessi può essere espressa come G, 2G, ... (n-1)G, dove G è la variazione annuale nella quantità dei pagamenti
0 1 2 3 ....... n
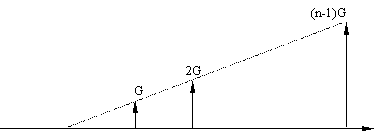
Un modo per la valutazione di una serie di questo tipo è quello di ridurre la serie di pagamenti uniformemente crescenti ad una serie equivalente di pagamenti annuali, in modo da poter poi usare il fattore della serie di pagamenti uguali.
Poniamo: I = investimento iniziale
G= variazione annuale o gradiente
n = numero di anni
A= pagamento annuo uguale equivalente
si può dimostrare che: ![]()
Esempio 1
Una persona progetta di risparmiare 1.000£ dal suo reddito nel corso di quest'anno, e pensa di aumentare questa somma di 200£ per ognuno dei successivi nove anni (la convenzione adottata è che la serie inizi alla fine del primo anno, mentre l'ultima somma risparmiata viene versata alla fine del decimo anno). Se l'interesse è dell'8%, calcolare il valore del pagamento annuale equivalente A.
La soluzione è: ![]() £ all'anno
£ all'anno

Esempio 2
Il fattore gradiente può essere anche impiegato per un gradiente uniforme decrescente.
Da un versamento iniziale di 5.000£, viene sottratta anno per anno una cifra pari a 600£ per 6 anni. Se l'interesse è 9%, la serie annuale uguale equivalente è:
A = 5.000 - 600 * (2,2498) = 3.650 £ all'anno , con i = 9% e n = 6
2.2.4. Il fattore della serie gradiente geometrico
In certi casi i pagamenti annuali aumentano o decrescono non di una somma costante, ma di una percentuale costante. L'andamento è rappresentato in figura, dove g viene usato per designare il cambiamento percentuale nell'ammontare dei pagamenti da un anno all'altro
0 1 2 3 n
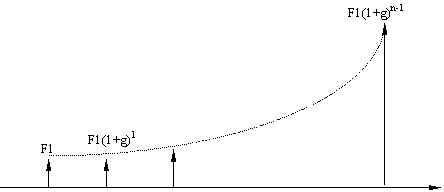
Quando g è positivo la serie aumenterà come in figura, quando g è negativo la serie è decrescente.
Si può dimostrare che il valore presente relativo a questa serie è:
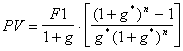 dove g*=
dove g*=![]()
Esempio
Un'impresa stima che le proprie entrate siano in aumento del 7% annuo da una base del primo anno di 360 M£. Il valore attuale di dieci anni di entrate di questo tipo ad un tasso d'interesse del 15% può essere calcolato come segue:
i = 15% g = 7% g* = 7,48 %
n= 10 PV = 360 M£ * [ (6,8704)/(1,07)] = 2.311 M£
2.3. Alcune considerazioni sulla frequenza della capitalizzazione
Per motivi di semplicità, ci siamo fondamentalmente occupati di periodi d'interesse solo di un anno. Tuttavia si possono effettuare accordi che prevedono pagamenti più frequenti degli interessi, ad esempio ogni semestre, trimestre o mese. Tali accordi determinano periodi d'interesse di un semestre, un trimestre o un mese e il calcolo degli interessi avviene, rispettivamente, due, quattro o dodici volte l'anno.
I tassi d'interesse, associati a questa capitalizzazione più frequente, vengono normalmente riferiti su base annuale secondo la seguente convenzione. Quando il tasso d'interesse reale o effettivo composto semestrale è del 3%, l'interesse annuale o nominale è definito come il "6% all'anno composto semestralmente". Analogamente, per un tasso d'interesse effettivo dell'1,5% composto alla fine di ogni periodo trimestrale, l'interesse nominale è definito come il "6% all'anno composto trimestralmente".
Quindi il tasso nominale d'interesse è espresso su base annuale e viene determinato moltiplicando il tasso d'interesse reale o effettivo tante volte quanti sono i periodi d'interesse di un anno.
2.3.1. Tassi di interesse nominali e effettivi
E' possibile stabilire una relazione fra il tasso d'interesse effettivo per ogni intervallo di tempo e il tasso di interesse nominale annuo. Siano:
r = tasso di interesse nominale per anno (o tasso annuo percentuale)
i = tasso d'interesse effettivo nell'intervallo di tempo
l = durata dell'intervallo di tempo in anni
m = reciproco della durata del periodo di capitalizzazione in anni
Il tasso d'interesse effettivo per ogni intervallo di tempo è dato da:
![]()
Se l'interesse è composto solo una volta nell'intervallo di tempo, allora lm =1 e quindi i=(r/m)
Seguono alcuni esempi:
Tasso nominale del 12% composto mensilmente con intervallo di tempo di un anno:
m=12 l = 1 r=0,12 i= 0,1268 o 12,68% all'anno
2) Tasso nominale del 12% composto mensilmente con intervallo di tempo di sei mesi:
m=12 l = 0,5 r=0,12 i= 0,0615 o 6,15% all'anno
3) Tasso nominale del 12% composto ogni sei mesi con intervallo di tempo di due anni:
m=2 l = 2 r=0,12 i= 0,2625 o 26,25% nei due anni
2.4. Un commento sul Present Value e sul Rischio
Il Valore Attuale di 400 M£ a un anno da oggi è, come abbiamo visto, minore di 400M£. Questa constatazione riflette i principio base della finanza secondo cui una lira oggi vale più di una lira domani, poiché la lira oggi può essere investita e iniziare a dare interessi immediatamente.
Il present value di un ricavo futuro può quindi essere ottenuto moltiplicando il ricavo per un fattore di sconto minore di uno:
PV = fattore di sconto Ricavo
Calcoliamo il PV di un'entrata di 400 M£ attesa ad un anno da oggi: questa deve essere scontata con il tasso di rendimento offerto da investimenti alternativi e confrontabili. Questo tasso di rendimento è spesso chiamato tasso di sconto o costo opportunità del capitale, poiché rappresenta la remunerazione a cui si rinuncia investendo nel progetto piuttosto che in attività a pari rischio. Se nel nostro esempio il tasso è pari al 7%:
PV = 400 M£ / 1,07 = 374 M£
E' importante notare che rappresenta il ricavo futuro atteso: la cifra di 400 M£ è un valore stimato, ma non è una certezza. Di questo fatto sono ben consci gli investitori: essi infatti possono ricevere 400 M£ con certezza acquistando oggi titoli di stato per 374 M£, quindi non investiranno nel progetto per lo stesso ammontare. Gli investitori cercano di evitare il rischio senza sacrificare il rendimento. Si può così enunciare un secondo principio base della finanza: una lira sicura vale più di una lira rischiosa.
In conclusione, i concetti di valore attuale e di tasso di sconto hanno ancora senso per investimenti rischiosi: è ancora corretto scontare le entrate con il tasso di rendimento offerto da investimenti comparabili. Dobbiamo però ragionare in termini di entrate attese e costi del capitale attesi.
2.5. Gli effetti dell'Inflazione
Lo studio dell'andamento economico della maggior parte dei sistemi di tutto il mondo, mostra che i prezzi dei beni e dei servizi fluttuano continuamente. Storicamente, con riferimento ai prezzi, la tendenza più comune è stata quella ascendente (inflazione), mentre vi sono stati episodi meno frequenti di discesa dei prezzi (deflazione). Questo mutamento dei prezzi influenza la quantità di beni e servizi che si possono acquistare con una data somma di denaro. Quando i prezzi aumentano, il potere di acquisto della moneta diminuisce, mentre prezzi decrescenti fanno aumentare il potere d'acquisto.
2.5.1. Misure dell'inflazione e della deflazione
Inflazione e deflazione sono termini che descrivono i mutamenti nel livello dei prezzi di un sistema economico. Senza far riferimento alle cause di tali variazioni, dedicheremo qui attenzione ai metodi necessari per determinare il tasso di variazione del livello dei prezzi. Poiché l'inflazione si è verificata assai più frequentemente della deflazione, useremo degli esempi che trattano principalmente questo caso.
I prezzi dei beni e dei servizi sono spinti verso l'alto o verso il basso per l'azione di numerosi fattori, che agiscono all'interno del sistema economico. Ad esempio, aumenti della produttività e nella disponibilità dei beni tendono a ridurre i prezzi, mentre alcuni strumenti di politica economica, come i sostegni dei prezzi e il finanziamento del deficit, tendono a farli aumentare. Quando tutti questi effetti sono considerati insieme, il risultato più frequente è che i prezzi aumentano.
Per misurare le variazioni nel tempo del livello dei prezzi relativamente a particolari beni di consumo è necessario un indice dei prezzi, cioè il rapporto tra il prezzo di un bene in un certo momento del tempo e il suo prezzo in un momento precedente. Il momento precedente del tempo è di solito un anno scelto come anno base, ad esempio:
Anno base: 1967 (indice dei prezzi IP 1967 = 100)
Prezzo del bene nel 1967 = 1460 £/Kg
Prezzo del bene nel 1993 = 5740 £/Kg
quindi:
IP 1993 = (5740/1460)*(100)= 393,2
questo valore di IP indica che il prezzo del 1993 è 3,932 volte più grande del prezzo del 1967.
Supponiamo ore che una persona possa investire al momento presente 100 K£, con l'aspettativa di guadagnare il 15% annualmente per i prossimi 5 anni. Alla fine dei 5 anni la somma accumulata sarà:
FV = 100 K£ * (2,011) = 201,1 K£
Attualmente, questa stessa persona può acquistare un pneumatico per auto che costa 100 K£, ma supponiamo che il prezzo dei pneumatici aumenti al tasso annuale del 10%. Alla fine dei 5 anni lo stesso pneumatico costerà:
FV = 100 K£ * (1,611) = 161,10 K£
Date queste condizioni, se il soggetto in esame ignorasse le variazioni dei prezzi, sarebbe fuorviato. Egli avrebbe l'errata impressione che se investisse adesso il denaro, al termine di 5 anni avrebbe la somma necessaria per acquistare due pneumatici. In realtà, con il denaro ricevuto dall'investimento, sarebbe in grado di acquistare solo (201/161)=1,25 pneumatici. Così, quando si considera il valore nel tempo della moneta, si deve includere l'effetto delle variazioni dei prezzi, cioè le variazioni nel potere di acquisto della moneta.
2.5.2. Il Tasso d'Inflazione
E' consuetudine utilizzare un tasso percentuale che rappresenti l'aumento o la diminuzione annuale dei prezzi nel corso di un periodo di tempo di un anno. Poichè il tasso ogni anno è basato sui prezzi dell'anno precedente, esso ha un effetto di capitalizzazione. Così, prezzi che sono cresciuti al tasso del 9% all'anno per il primo anno e dell'8% all'anno l'anno successivo, avranno un valore alla fine del secondo anno di:
[prezzi alla fine 2° anno]=(1+0,09)*(1+0,08)*[prezzi all'inizio 1° anno]
Per il calcolo del tasso annuale di aumento dei prezzi si possono utilizzare i valori dell'indice dei prezzi:
Tasso Annuale d'Inflazione per l'anno (t+1)=![]()
Se per esempio sono noti gli indici dei prezzi relativi agli anni 1979 e 1980, si può valutare il
Tasso annuale d'inflazione per il 1980 = (246,8 - 217,4) / 217,4 = 0,135 o 13,5 %
La maggior parte degli studi economici richiede l'impiego di stime che dipendono dalle aspettative sui tassi di inflazione futuri. La determinazione di questi tassi futuri deve essere basata sui trend dei tassi riferiti al passato, nonché alle condizioni economiche previste. Così come la stima dei futuri flussi di cassa , anche la previsione accurata dei tassi d'inflazione futuri è un'impresa difficile.
Molti studi impiegano un tasso d'inflazione annuale medio quando la durata dell'investimento è lunga. Questo sistema richiede la stima di un singolo tasso medio che rappresenti un insieme di singoli tassi annuali, che può essere ricavato attraverso l'espressione:
IP t (1+fm)n = IP t+n
dove fm = tasso annuale medio d'inflazione
n = numero di anni
Quindi noti gli IP degli anni 1972 e 1980 ( 8 anni ), il tasso medio d'inflazione è stato:
125,3 (1+fm)8 = 246,8 fm = 8,8 % annuo
2.5.3. Come si considerano gli effetti dell'inflazione
Esistono due metodi fondamentali che permettono di considerare allo stesso tempo le variazioni della capacità reddituale del denaro e del suo potere d'acquisto: il primo ipotizza che i flussi di cassa vengano misurati in termini di lire correnti (ed è il metodo che abbiamo fin qui seguito); il secondo impiega il concetto di lire costanti. Naturalmente questi sistemi sono tra loro coerenti e, se vengono applicati correttamente, conducono a identiche conclusioni
2.5.3.1. Definizioni di i, i', f
Per sviluppare le relazioni che intercorrono tra l'analisi a lire costanti e quella a lire correnti, sono necessarie alcune precise definizioni per i diversi tassi d'interesse da usare nei calcoli.
Il tasso di interesse di mercato i (o tasso di interesse a lire correnti) rappresenta l'opportunità reddituale data dall'impiego del denaro che si riflette nei tassi d'interesse correnti disponibili sul mercato. Poiché si ipotizza un comportamento razionale degli operatori, essi saranno ben consapevoli della capacità reddituale del denaro e degli effetti negativi dell'inflazione: quando il tasso d'inflazione aumenta, c'è di solito un corrispondente movimento verso l'alto dei tassi d'interesse. Dal momento che per quanto detto nei capitoli precedenti, i flussi di cassa vengono espressi in termini di lire correnti, il tasso fin qui impiegato nei calcoli è il tasso d'interesse di mercato. Quando un'impresa stabilisce il suo tasso di rendimento minimo desiderato si tratta di solito di un tasso di interesse di mercato che esprime di fatto un concetto di costo/opportunità di capitale.
Il tasso di interesse deflazionato i' (o tasso di interesse a lire costanti, tasso d'interesse reale) rappresenta la capacità reddituale del denaro detratti gli effetti dell'inflazione. Questo tasso è un'astrazione e non è direttamente noto al pubblico: deve quindi essere calcolato, poiché in genere non viene usato nelle transizioni dei mercati finanziari. Se non c'è inflazione, allora il tasso di interesse di mercato e il tasso di interesse deflazionato sono identici.
Il tasso di inflazione f (o tasso di crescita, tasso di aumento del costo della vita) è la percentuale annuale di crescita dei prezzi di beni e servizi, come visto nei paragrafi precedenti.
Quando si usa uno di questi tre tassi, dobbiamo essere consapevoli che i loro valori saranno basati su stime, che riflettono aspettative future.
2.5.3.2. Rappresentazione dei flussi di cassa in lire correnti o costanti
Le lire correnti rappresentano le lire che si ricevono o si cedono in ogni momento del tempo. I flussi di cassa valutati nei capitoli precedenti sono espressi in termini di lire correnti.
Le lire costanti rappresentano il potere di acquisto ipotetico di entrate e uscite future in termini del potere d'acquisto delle lire in un certo anno base. Questo anno base può essere scelto arbitrariamente, sebbene solitamente si assuma che il tempo zero sia l'inizio dell'investimento (nelle analisi seguenti l'anno base è l'anno zero, a meno che non venga specificato altrimenti).
Un flusso di cassa può essere espresso in termini di lire correnti sia per diretta espressione in lire correnti che per conversione delle stime a lire costanti in lire correnti. Analogo discorso vale per le lire costanti. Se è richiesta la trasformazione delle lire correnti, ad un particolare momento del tempo, in lire costanti (basata sul potere d'acquisto relativo a n anni precedenti) allo momento del tempo, si ha :
lire costanti = [ 1 / (1+f) n ]* lire correnti
dove f è il tasso percentuale annuale d'inflazione e n il numero di anni.
Consideriamo la trasformazione di 1000 £ correnti del 1985, in lire costanti al 1985, prendendo come anno base il 1967 :
n = 18 anni noto il tasso annuale medio di inflazione nei 18 anni tra il '67 e il '85 : f= 6,7%
lire costanti = [ 1 / (1,067) 18 ]* 1000 £ = 311 £ 2.5.3.3. Relazione tra lire correnti e costanti
La figura sotto presenta una singola entrata di cassa al tempo n (espresso in anni) successivo al presente (tempo 0). Questa entrata è mostrata come F in termini di lire correnti e come F' in termini di lire costanti.
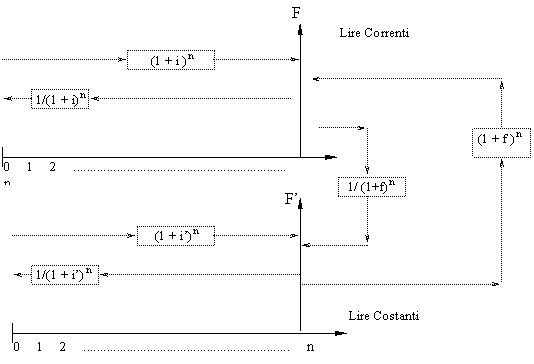
Se il tasso d'inflazione previsto è f, è stato mostrato nel paragrafo precedente che il fattore 1/(1+f)n trasforma il flusso di cassa F al tempo n in lire correnti in flusso di cassa F' al tempo n in lire costanti.
Se l'anno base scelto non fosse stato il tempo 0 (supponiamo che risalga a 2 anni prima dell'anno in corso), il fattore per convertire lire correnti in lire costanti al tempo n dal presente sarebbe stato 1/(1+f) n+2.
Qundi, il tasso d'inflazione f è necessario per trasformare le lire espresse tramite l'una o l'altra forma, allo stesso momento del tempo.
Per trasformare le lire nel loro equivalente in lire correnti in differenti momenti nel tempo, si usa il tasso di interesse di mercato i, come rappresentato in figura.
Quindi per valori espressi in lire correnti, il tasso d'interesse di mercato i viene usato per calcolare le equivalenze.
Come mostrato in figura, il tasso deflazionato i' è la base per calcolare le equivalenze per valori espressi in lire costanti. Il fattore 1/(1+i') n trova l'equivalenza a lire costanti nel tempo t=0 del flusso di cassa costante in t=n. Poiché gli effetti inflattivi sono stati rimossi dai flussi di cassa espressi in lire costanti, i calcoli relativi alla capacità reddituale del denaro devono applicare un tasso di interesse che sia libero dagli effetti dell'inflazione.
Quando si calcolano le equivalenze per valori espressi in lire costanti, si deve impiegare i', cioè il tasso al netto dell'inflazione.
Possiamo ottenere la relazione tra i, i' e f osservando che, se l'anno base a lire costanti è il tempo zero, allora al tempo zero lire costanti e lire correnti hanno identico potere d'acquisto, cioè le lire correnti nell'anno base potranno acquistare gli stessi beni e servizi delle lire costanti. Solo nell'anno base si verifica questa trasformazione alla pari tra lire correnti e lire costanti.
Perché un'analisi svolta sia in termini di lire correnti, sia in termini di lire costanti sia corretta, la somma equivalente nell'anno base deve essere uguale indipendentemente dagli indici di valore considerati. Iniziando al tempo t=n con F espresso in lire correnti, il calcolo del suo equivalente in t=0 può essere realizzato in due modi. Il primo utilizza lire correnti e le trasforma nel loro equivalente in t=0, anno base considerato
P = F / (1 + i) n
Il secondo metodo trasforma le lire correnti in lire costanti e poi trova l'equivalente di quella somma in lire costanti in t=0 :
F' = F / (1 + f) n
P = F' / (1 + i') n = F / [(1 + f) n * (1 + i') n]
Poiché i valori di P nell'anno base devono essere uguali, uguagliando le due espressioni di P sopra ottenute si ottiene:
i = (1 + f) * (1 + i') - 1
Risolvendo per i' si ricava:
i' = [(1+i) / (1+f)] - 1
Come esempio, supponiamo di considerare un tasso di inflazione annuo del 10%, mentre il tasso di interesse di mercato sia noto e pari a 15% l'anno. Trovando i' si ha:
i'
Se una singola entrata di 100 M£ si riceve tra 12 anni, qual è l'equivalente di questa entrata al tempo t=0 ?
P = F / (1 + i) n = P = 100 M£ / (1 + 0,15) 12 = 18,69 M£
oppure
P = F / [(1 + f) n * (1 + i') n] = 100 M£ / [(1 + 0,10) 12 * (1 + 0,0455) 12] = 18,69 M£
Il metodo scelto varierà a seconda che il risultato debba essere presentato in lire correnti o costanti, che le stime sul flusso di cassa siano in lire correnti o costanti, e dalla facilità nell'eseguire i calcoli.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025