Analisi degli investimenti in condizioni di incertezza

dove R^*= valore atteso

FC_i = flusso di cassa associato al i-esimo evento

P _i = probabilità di accadimento del i-esimo evento

N = numero di possibili eventi

La dispersione dei dati della distribuzione probabilistica intorno al valor medio è un indice del rischio associato al progetto. La statistica fornisce svariati strumenti per la valutazione della dispersione, tra cui noi useremo :

Varianza s =

Deviazione Standard s =

Coefficiente di variazione u s / R^*

Esempio

Si vogliono confrontare due alternative di investimento e, in relazione all'andamento dell'economia atteso nell'anno 1995, si abbia un prospetto del tipo :

Flussi di Cassa attesi

Andamento Economico   Probabilità Evento Invest. A Invest.B

1-Crescita  0,3 1800 1600

2-Moderata Crescita 0,5 1500 1200

3-Recessione 0,2 800 1000

Per entrambe gli investimenti bisogna valutare :

Valore Medio Atteso R^*=

quindi per l'investimento A : R^*_A = 0,3*1800+0,5*1500+0,2*800 = 1450 £

investimento B : R^*_B = 0,3*1600+0,5*1200+0,2*1000 = 1280 £

Quindi i valori attesi dei due investimenti sono determinati pesando i flussi di cassa con la rispettiva probabilità che si verifichi un determinato stato dell'economia.

Una misura del rischio associato ai due investimenti è data dalla valutazione di :

Varianza e Deviazione Standard

investimento A : s s = =

investimento B : s s ==

La deviazione standard (e la varianza che ne è il quadrato) sono un indice di quanto il valore atteso sia rappresentativo della distribuzione: quanto più è elevata la deviazione standard, tanto meno rappresentativo è il valor medio, in quanto la distribuzione è molto dispersa intorno a tale valore.

Nella pratica la deviazione standard è l'indice più usato poiché presenta la stessa unità di 727j94h misura [$] del valore atteso: queste due grandezze definiscono in maniera esaustiva una distribuzione probabilistica. 

Coefficiente di variazione

investimento A : u

investimento B : u

Il coefficiente di variazione mostra quindi la rischiosità (misurata attraverso la deviazione standard) per ogni dollaro atteso di ritorno :

u basso bassa rischiosità dell'investimento ( FC quasi certi)

u elevato alta rischiosità dell'investimento ( FC molto incerti)

4.2. L'albero decisionale

Una tecnica raccomandata per risolvere problemi articolati e complessi è quella dell'albero decisionale. Si tratta di una rappresentazione grafica che permette di evidenziare le diverse alternative che si articolano da un punto comune, ognuna delle quali è caratterizzata da una certa probabilità di accadimento. Il seguente esempio esporrà in modo chiaro quanto appena affermato.

Esempio

Una società sta considerando sta considerando due alternative di investimento per l'anno 1990 (single-period investiments), i ritorni dei quali dipendono dallo stato dell'economia atteso nell'anno stesso.

Lo stato dell'economia è noto solo attraverso una distribuzione probabilistica :

I ritorni di ogni alternativa in ogni possibile stato economico sono:

Usando l'albero decisionale individuare l'alternativa che consente di massimizzare i ritorni

SOLUZIONE

La soluzione al problema è tutta contenuta nell'albero decisionale rappresentato. Sull'estrema destra i ritorni di ogni stato dell'economia sono stati pesati con la corrispondente probabilità di accadimento. La somma di tutti questi valori calcolati fornisce il ritorno atteso dello specifico progetto. Poiché l'obiettivo era quello di massimizzare i ritorni il progetto B risulta essere il migliore con 52£, contro i 44£ del progetto A.

Il diagramma ad albero può essere anche utilizzato per effettuare delle valutazioni su un singolo progetto che si articola su più periodi temporali: naturalmente ora, oltre a considerare la probabilità di accadimento degli eventi, sarà necessario attualizzare i flussi di cassa.

Per definizione, il valore atteso dei flussi di cassa attualizzati è :

A^* =

La deviazione standard dei flussi di cassa scontati è

s _A =

dove A _S è flusso di cassa scontato con probabilità di accadimento P_S .

Applichiamo queste due formule ad un esempio: si consideri un progetto P con vita utile di 3 anni. I possibili flussi di cassa in entrata per ogni periodo (che sono già stati scontati per riportarli al presente) e le loro probabilità di accadimento associate sono le seguenti:

dove P[A^S₂ /A^S₁] è la probabilità composta che avvenga l'evento A^S₂ soggetta all'avverarsi dell'evento A^S₁.

Utilizzando i dati sopra riportati, determinare il valore atteso di flusso di cassa e la deviazione standard.

SOLUZIONE

Valore Atteso

Ci serviamo di una tabella del tipo :

Periodo 1 Periodo 2 Periodo 3

Quindi :

A^* = = 287.745 $

Deviazione Standard

Ci serviamo di una tabella del tipo :

da cui    s

Equivalente Certo (CE)

Con il metodo dell'equivalente certo, i valori stimati dei flussi di cassa ad ogni anno (che rappresenta il valore atteso di una distribuzione probabilistica di cash flow), vengono moltiplicati per un Coefficiente di Certezza Equivalente (CEC), che ingloba il grado di rischio associato alla distribuzione di FC stimata. Il CEC varia da 0 a 1: il suo valore è tanto più elevato quanto è minore l'incertezza legata alla distribuzione dei FC.

Con il metodo dell'Equivalente Certo, la bontà di un progetto si valuta in maniera del tutto analoga a quanto visto con NPV : non vengono cioè accettati gli investimenti che presentano CE minore di zero. In questo caso l'espressione di attualizzazione dei flussi di cassa assume la forma :

Equivalente Certo Atteso = CE =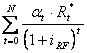

dove   R_t^* = flusso di cassa atteso al periodo t

a_t = valore del CEC al periodo t, ottenuto, attraverso opportune tabelle, in funzione del rischio associato alla distribuzione dei FC (valutato con il coefficiente di variazione u a_t 1 con a a (t, u, tipologia di investimento) su Tabelle

i _RF = tasso di sconto risk-free, che si assume costante lungo la vita utile del progetto

N = vita utile del progetto

Esempio

La Società ABC vuole valutare la bontà di un nuovo investimento, di cui sono stati precedentemente stimati i valori attesi e le deviazioni standard nei vari anni di vita utile :

L'esborso iniziale è di 3000£ e il tasso di sconto risk-free è pari al 6%. Stabilire l'accettabilità del progetto utilizzando il metodo dell'equivalente certo.

SOLUZIONE

Ci serviamo della seguente tabella per valutare CE:

Essendo CE>0, allora il progetto viene accettato.

Risk-Adjusted Discount Rate (RAR

Anche questo metodo si basa sulla proposizione che i progetti che presentano elevata variabilità nella distribuzione probabilistica dei flussi di cassa, devono attualizzare i propri FC con un tasso di sconto superiore rispetto a investimenti con minor variabilità o rischio.

Il tasso di sconto può essere quindi essere espresso come:

r = i_RF + u + a

dove    r = risk-adjusted discount rate (tasso di sconto modificato per tener conto del rischio)

i_RF = tasso di sconto risk-free

u = rischiosità standard dell'impresa

a = correzione legata alla rischiosità dello specifico investimento da apportare al valore di u. In particolare a può essere positivo o negativo a seconda che il rischio del progetto in esame sia maggiore o minore del rischio medio u dei progetti dell'impresa

Il valore presente atteso valutato col metodo risk-adjusted discount rate è espresso come :

RAR =

La tabella sotto riporta un esempio di valutazione del premio di rischio i_R=u+a per la Società ABC. L'ammontare della correzione per rischio scelta dall'impresa riflette la maggior o minor avversione al rischio che guidano le decisioni strategiche dell'azienda: si noti che rispetto alla valutazione di CEC, in questo caso si valutano generalmente i tassi di sconto indipendentemente dal periodo temporale di vita utile del progetto.

Esempio

La Società XMT sta analizzando un progetto in ricerca e sviluppo, che prevede un esborso iniziale di 5000 £. Sono stati stimati i valori attesi e le deviazioni standard dei ritorni negli anni di vita utile :

Il tasso di sconto risk-free è pari al 10%. Stabilire l'accettabilità del progetto utilizzando il metodo RAR.

SOLUZIONE

Nel caso di investimenti di "Ricerca e Sviluppo" con u<0.2 il coefficiente r è pari a :

risk-adjusted discount rate r = i_RF + 10% = 20%

Quindi :

RAR = -5000 + 1500/1.2 + 1000/1.2² + 2500/1.2³ + 2000/1.2⁴ = -644 £

Poiché il RAR è negativo, il progetto non deve essere accettato.

E' opportuno evidenziare alcuni aspetti del metodo RAR che sono stati soggetti a critica:

Il metodo considera solo la rischiosità associata ad una generale categoria di progetti, tascurando il variare del rischio durante la vita utile dell'investimento.

Il metodo combina due parametri nel processo di attualizzazione: il tasso risk-free e il premio per il rischio. In particolare l'utilizzo di un premio elevato costante lungo l'intera vita utile penalizza pesantemente i flussi di cassa molto in avanti nel tempo, secondo il fattore 1/(1+r)^t