|
|
| |
RELAZIONE DI ELETTRONICA
OBIETTIVO DELLA PROVA
Simulazione al computer della seguente rete combinatoria:
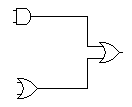
Da questa rete è abbiamo dovuto:
-& 222h79c nbsp; & 222h79c nbsp; ricavare l'espressione logica: Y = A * B + C + D
-& 222h79c nbsp; & 222h79c nbsp; costruire la tabella di verità (vedi contenuti della prova)
-& 222h79c nbsp; & 222h79c nbsp; disegnare il circuito nel programma di simulazione al computer con i rispettivi componenti e provare l'effettiva validità delle funzioni logiche tramite l'utilizzo del led (in Multisim)
STRUMENTI PRINCIPALI UTILIZZATI NELLA PROVA
-& 222h79c nbsp; & 222h79c nbsp; Elaboratore
Essendo una prova simulata tutte le operazioni sono state svolte al computer.
-& 222h79c nbsp; & 222h79c nbsp; Editor testuale
Ho utilizzato il programma Microsoft Word per
scrivere la relazione e per dare una impostazione ad essa. Oltre alla stesura
il programma ci ha permesso di inserire la tabella di verità e le immagini
necessarie per descrivere opportunamente il tutto.
Si presenta con un ambiente di questo tipo:
-& 222h79c nbsp; & 222h79c nbsp; Editor grafico (raster)
Ho utilizzato Paint Shop Pro che mi ha permesso di modificare e "ritagliare" l'immagine importata da Multisim nella clipboard di Windows e ricopiarla nuovamente per poi poterla immettere in Word.
Si presenta con un ambiente di questo tipo:
-& 222h79c nbsp; & 222h79c nbsp; Programma per il disegno e la progettazione di reti combinatorie
Multisim è lo strumento principale che ci ha permesso di disegnare la rete combinatoria con tutti i suoi componenti. Esso è dotato di vari menu necessari per trasferire i "componenti" nel "foglio di lavoro" ovvero un ambiente che sostituisce, in modo concettuale, il classico circuito stampato o quello per montaggi sperimentali (bread board).
Si presenta con un ambiente di questo tipo:
MODALITA' DI ESECUZIONE DELLA PROVA
In primo luogo abbiamo disegnato in Work Bench il circuito assegnato dal professore (fig. 1).
Per realizzarlo è stato necessario utilizzare i seguenti componenti:
-& 222h79c nbsp; & 222h79c nbsp; 1 Generatore da 5 V
-& 222h79c nbsp; & 222h79c nbsp; 1 Massa
-& 222h79c nbsp; & 222h79c nbsp; 4 Switch
-& 222h79c nbsp; & 222h79c nbsp; 2 porte logiche OR
-& 222h79c nbsp; & 222h79c nbsp; 1 porta logica AND
-& 222h79c nbsp; & 222h79c nbsp; 1 resistenza da 100 W
-& 222h79c nbsp; & 222h79c nbsp; 1 diodo-led
-& 222h79c nbsp; & 222h79c nbsp; vari fili conduttori
-& 222h79c nbsp; & 222h79c nbsp; 7 connettori per la creazione di nodi
Realizzato il circuito abbiamo costruito la tabella della verità (vedi contenuti della prova); avendo tre porte logiche per costruirla abbiamo dovuto utilizzare 16 (24) numeri in notazione binaria partendo dallo 00002 (010) fino ad arrivare a 11112 (1510).
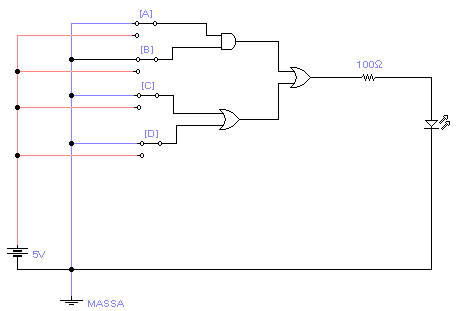
Figura n. 1:
CONTENUTI DELLA PROVA
Nei contenuti della prova allego l'espressione logica ricavata e la tabella di verità:
Y = A * B + C + D
|
A |
B |
C |
D |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CONSIDERAZIONI TEORICHE
SISTEMA DI NUMERAZIONE BINARIO
Il sistema di numerazione binario (in base 2) è quello comprensibile alle porte logiche presenti nei circuiti integrati. Grazie a questa notazione è possibile realizzare una vasta gamma di funzioni logiche.
Il sistema di numerazione binario è un sistema posizionale come quello decimale: consideriamo il numero decimale 237 , esso può essere scomposto in questo modo:
ossia le cifre del numero vengono moltiplicate per le potenze di dieci (da cui decimale) crescenti da destra verso sinistra. I numeri binari vengono costruiti nello stesso modo solo che invece di potenze di 10 si usano le potenze di 2, quindi considerando il seguente numero binario, scomponendolo ed effettuando i calcoli si ottiene il corrispondente numero decimale:
FUNZIONI LOGICHE ELEMENTARI
Nel nostro circuito abbiamo utilizzato due tipi di porte logiche:
-& 222h79c nbsp; & 222h79c nbsp; AND (la cui espressione logica è Y = A * B)
La porta AND è una porta elementare. La sua tabella di verità è:
A B | Y
A e B rappresentano i due valori di entrata mentre la Y è l'uscita che si ha a secondo della combinazione. Il valore 0 corrisponde all'assenza ed il valore 1 alla presenza di corrente nella rete.
-& 222h79c nbsp; & 222h79c nbsp; OR (la cui espressione logica è Y = A + B)
La porta OR è anch'essa una porta elementare. La sua tabella di verità è:
A B | Y
OSSERVAZIONI FINALI: Il nostro compito è stato quello di dimostrare che l'uscita (Y) corrisponde al passaggio di corrente (nella rete) quando il valore è 1 (es. 0101) e alla assenza di corrente quando il valore è 0 (es. 1000). Abbiamo potuto verificare questo grazie al led posto nel simulatore della rete combinatoria:
come si può notare in figura 2 il led è acceso perché la combinazione di valori usati (0101) da come risultato 1.
Analizziamo perché: [ 0 AND 1 = 0 ] OR [ 0 OR 1 = 1 ] = 1
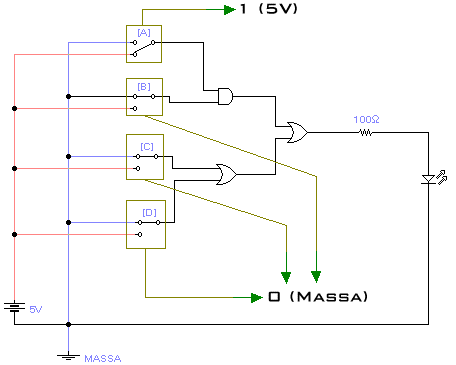
Quando invece la combinazione è 1000 (figura 2):
Il led non si accende.
Analizziamo perché: [ 1 AND 0 = 0 ] OR [ 0 OR 0 = 0 ] = 0
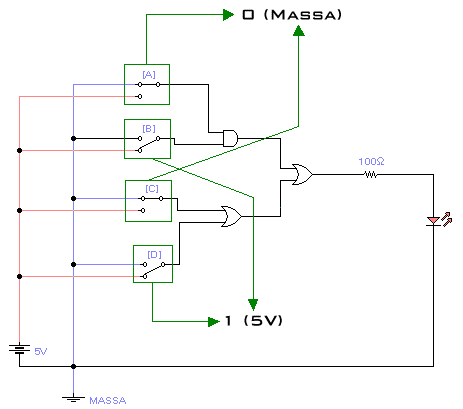
Figura n. 1:
Figura n. 2:
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026