|
|
| |
pressione acustica E' definita come Dp = p-p0 con Dp<<p0. p0 e p sono rispettivamente la pressione dell'aria a riposo e sotto eccitazione acustica.
velocità di vibrazione Differenze di
pressione in due punti corrispondono ad una forza diretta secondo il gradiente
di pressione ![]() che sarà causa del
moto dell'elemento di volume dV di massa dm=r dV (r è la densità dell'aria) con una velocità
che sarà causa del
moto dell'elemento di volume dV di massa dm=r dV (r è la densità dell'aria) con una velocità ![]() ricavabile
dall'equazione delle forze:
ricavabile
dall'equazione delle forze:
![]() (1)
(1)
energia sonora i 333d34d n un punto Se ad un
elemento di volume dV viene applicata una forza per uno spostamento
infinitesimo ![]() , il campo sonoro (ovvero la forza) produrrà lavoro e quindi
in quel punto il campo avrà una certa energia
, il campo sonoro (ovvero la forza) produrrà lavoro e quindi
in quel punto il campo avrà una certa energia ![]() . Contemporaneamente anche il volumetto d'aria avrà
un'energia cinetica variabile che verrà scambiata nel tempo con quella del
campo sonoro[1]. Questa
energia varia col tempo perché varia sia la forza che lo spostamento (che è
legato alla forza e alla massa del volumetto).
. Contemporaneamente anche il volumetto d'aria avrà
un'energia cinetica variabile che verrà scambiata nel tempo con quella del
campo sonoro[1]. Questa
energia varia col tempo perché varia sia la forza che lo spostamento (che è
legato alla forza e alla massa del volumetto).
potenza acustica in un punto La potenza W è la variazione di energia per unità di tempo (energia assorbita per unità di tempo), supponendo però che la forza che produce/assorbe energia si mantenga costante durante il tempo in cui si calcola la variazione di energia, quindi:
![]()
Nei
casi particolari di onde acustiche piane o sferiche, essendo l'onda
longitudinale, ![]() e
e ![]() hanno la stessa
direzione (asse di propagazione per le onde piane e asse radiale per le onde
sferiche) e quindi si ha:
hanno la stessa
direzione (asse di propagazione per le onde piane e asse radiale per le onde
sferiche) e quindi si ha:
dW = d(Dp)u dS
intensità acustica in un punto Se il campo
sonoro si propaga sotto forma di onde, allora anche l'energia avrà una
dipendenza spazio-temporale di tipo a onda, per cui possiamo dire che anch'essa
si propaga. L'intensità acustica è l'energia per unità di superficie e di tempo
che fluisce nella direzione di propagazione dell'onda; quindi è una ![]() tale che:
tale che:
P(x+dx,y+dy,z+dz)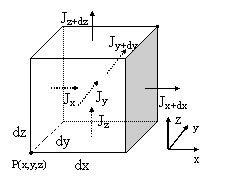
![]()
Quindi
per il teorema della divergenza ![]() dunque
dunque ![]()
Possiamo vedere ciò anche considerando un volumetto infinitesimo dV corrispondente ad un punto P(x,y,z). La potenza istantanea dW relativa ad esso sarà pari al flusso di energia entrante da tutte e sei le facce, ovvero, se orientiamo le facce secondo le x, y e z crescenti:
dW = (Jx-Jx+dx)dydz + (Jy-Jy+dy)dxdz
+ (Jz-Jz+dz)dxdy ![]()
L'ultima uguaglianza si verifica moltiplicando e dividendo i membri della somma per dx, dy e dz rispettivamente. Inoltre, se orientiamo il volumetto nella direzione di oscillazione, supponendo anche che è la stessa del gradiente di pressione (onda longitudinale) e facciamo coincidere questa direzione con quella dell'asse x, avremo:
dW = (Jx - Jx+dx)dydz =![]()
Da qui si vede chiaramente che Jx = Dpx u
notazione complessa Avendo a che fare con grandezze che oscillano armonicamente, è conveniente
trattarle associandovi altre grandezze complesse corrispondenti. Un modo
possibile di fare questo è il seguente: data una grandezza armonica x(r,t) = ![]() , vi associamo
, vi associamo ![]() in modo tale che
in modo tale che ![]()
Vediamo per esempio la pressione nei casi di onde piane e sferiche:
onde piane: Dp = Pmsin(wt-kx+j > ![]()
onde sferiche: Dp = ![]() sin(wt-kr+j >
sin(wt-kr+j > ![]()
Per calcolare invece la velocità
ricorriamo alla (1), che nel caso di onde piane e sferiche ci porta
rispettivamente a ![]() e
e ![]() . Sviluppando i calcoli e imponendo le opportune condizioni
al contorno si ricava, per le onde piane:
. Sviluppando i calcoli e imponendo le opportune condizioni
al contorno si ricava, per le onde piane:
u
= ![]() sin(wt-kx+j >
sin(wt-kx+j > ![]()
E per quelle sferiche:
u=![]() >U=
>U=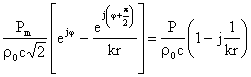
valore medio dell'intensità per onde armoniche Normalmente, quando si parla di energia, potenza e intensità di onde armoniche piane o sferiche, ci si riferisce non ai valori istantanei sopra considerati ma ai loro valori medi su un periodo. Per esempio, andando a calcolare il valor medio dell'intensità per un'onda piana o sferica, dovremo integrare il prodotto Dp u su un periodo. Sappiamo, dalla teoria dei circuiti, che utilizzando le grandezze complesse risulta:
![]()
Quindi avremo rispettivamente, nei casi di onde piane e sferiche:
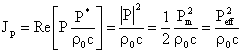
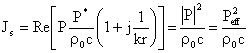
Ad esempio il caso di oscillazione armonica delle particelle d'aria è identico a quello di un oscillatore armonico con un corpo di massa m e una molla di costante elastica k in cui l'energia del campo di forze elastico viene trasferita alla massa come energia cinetica e viceversa, in un continuo (in assenza di attrito) palleggio.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026