|
|
| |
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"CAMMA E BILANCERE"
E' dato il meccanismo di figura. E' assegnata la forza Q esercitata sull'asta 4.
Tutta la geometria del sistema è nota, in particolare sono noti i raggi dei circoli d'attrito delle coppie rotoidali, il parametro di attrito volvente d, gli angoli di attrito j j j
Si chiede di determinare il valore del momento motore da applicare alla camma.
Svolgimento.
Nel sistema considerato i gradi di libertà sono due, uno dei quali è superfluo perché è dato dal rotolamento della rotella: si ha quindi un solo grado effettivo di libertà.
Se consideriamo il problema senza attrito, il momento risultante delle forze applicate alla camma è nullo, in quanto agiscono forze uguali e contrarie agenti sulla stessa retta di azione e quindi con braccio nullo. Se c'è invece attrito, questi fa cambiare l'inclinazione delle rette d'azione delle reazioni agenti sui vari elementi del sistema.
Il problema si risolve individuando graficamente l'inclinazione delle rette d'azione in presenza di attrito rispetto alle rette senza attrito. La soluzione è grafica, come si vede nell'allegato A, fino all'individuazione, in modulo e in verso, delle reazioni R51 ed R21 formanti la coppia motrice da applicare alla camma.
Si studia l'equilibrio dei vari elementi che compongono il sistema, considerando il verso del moto istantaneo in modo tale da trovare la direzione delle rette d'azione in funzione degli angoli di attrito noti.
Sull'elemento "4" agiscono :
- la forza applicata Q (350 N),
- le reazioni R54, R5'4, R34, che vengono trovate, dopo aver individuato le rette d'azione, mediante gli angoli di attrito j j j e le varie ipotesi sul moto con l'applicazione del metodo della retta ausiliaria. Sono trovati così i moduli di tali reazioni e i versi.
Sull'elemento "3" agiscono la R43 , uguale ed opposta alla R34, la R23 e la R53.
La retta d'azione della R23 è data dall'intersezione della retta passante per il punto individuato dal parametro d dell'attrito volvente e tangente al circolo di attrito sull'elemento "2". L'intersezione della retta di azione di R23 e quella di R43 individuano il punto P dal quale parte la retta di azione di R53 che è tangente al circolo di attrito sull'elemento "5". Applicando la regola del parallelogramma si trovano i moduli di tali reazioni.
Sull'elemento "1" agiscono le reazioni R21, opposta alla R23, e la R51 parallela alla R21 e tangente al circolo di attrito in modo da formare una coppia che si oppone al moto.
Si ricava il braccio b di tale coppia e si calcola il momento motore M = R51 * b.
Tabella dei risultati
|
Q = 350 N |
j j j |
|
d = 2 mm |
R51 = 610 N |
|
R23 = 610 N |
R43 = 358 N |
|
R34 = 385 N |
R53 = 960 N |
|
R5'4 = 120 N |
b = 16 cm = 0.016 m |
|
M = R51 * b = 9.76 N m |
R54 = 360 N |
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
AUTOTRENO IN SALITA
Un autotreno avanza lungo una salita di pendenza p nota. Sono assegnate tutte le dimensioni geometriche della motrice e del rimorchio, in particolare gli interassi i e i raggi R delle ruote, i pesi della motrice Qm e del rimorchio Qr, le loro linee d'azione, l'altezza h sul suolo del gancio di traino, i parametri dell'attrito volvente d nei contatti tra il suolo e le diverse ruote, gli angoli ja di aderenza nei contatti ruota-terreno, i raggi r dei circoli di attrito dei perni di tutte le ruote.
Determinare il momento motore che è necessario applicare alle ruote motrici (siano quelle posteriori della motrice) per far avanzare il veicolo con velocità costante.
Dati :
|
Qm |
KN |
|
Qr |
KN |
|
ja |
p rad |
|
im |
3,7 m |
|
ir |
5 m |
|
R |
0,6 m |
|
h |
2,1 R = 1,26 m |
|
r |
2mm |
|
d |
3mm |
|
p |
|
Nel disegno :
r = 2 mm
d = 3 mm
Svolgimento
a) Equilibrio del rimorchio.
Si tracciano le rette di azione delle forze agenti sul rimorchio :
- il peso Qr ( per ipotesi passa per la mezzeria dell'interasse ir ),
- lo sforzo di trazione T trasmesso dalla motrice (la retta passa per il gancio posto ad altezza h),
- le reazioni del terreno sulle ruote anteriori e posteriori Ra e Rp (le rette passano per il punto di tangenza al circolo d'attrito e il parametro dell'attrito volvente).
L'intersezione di queste rette individuano i punti H e K per i quali passa la retta ausiliaria, tramite la quale si calcolano le intensità di Ra , Rp e T.
b) Equilibrio della motrice.
Tramite la -T, si traccia la risultante S (poiché Qm è noto) ; tracciando la retta d'azione di S si trova il punto K' intersezione delle rette d'azione R'a e R'p (R'a poiché è una ruota condotta si può applicare il procedimento precedente, R'p poiché su una ruota motrice, la sua retta e una retta passante per d'p con un'inclinazione j), si trovano così le intensità delle varie reazioni. Nota R'p si trova il momento motore cercato :
M = R'p * b.
La soluzione grafica ha fornito i seguenti risultati :
|
Ra |
= 70 KN |
|
Rp |
= 54 KN |
|
R'a |
= 24 KN |
|
R'p |
= 122 KN |
|
T |
= 60 KN |
|
b |
= 0,6 m |
|
Mm |
= R'p*b = 73,2 KN*m = 73200 N*m = 73200 J |
La reazione R'p risulta inclinata di un angolo j minore di ja p/4, quindi è verificata la condizione di non slittamento.
In questo caso non si ha ribaltamento in quanto la R'a del terreno è rivolta verso l'alto.
In termini di equilibrio di forze, ciò che ostacola lo slittamento, favorisce il ribaltamento. Nella pratica si cerca di evitare il ribaltamento sia lavorando sulle forze e sui parametri geometrici che le determinano (quali la posizione dei baricentri e le altezze dei ganci), sia limitando lo slittamento mediante l'aumento di ja
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
DIMENSIONAMENTO DI UN CUSCINETTO A LUBRIFICAZIONE IDRODINAMICA
Con i dati sotto riportati si dimensioni il cuscinetto (determinare L, D, C) e si trovino i parametri di funzionamento h0, f, Qs, Tm. Si consideri il cuscinetto completo e con L/D = 1. Sono allegati i diagrammi di Raimondi e Boyd per questo tipo di cuscinetto.
Dati
|
Ra |
mm |
|
r |
= 830 Kg/m3 |
|
c |
= 1700 J/ Kg*K |
|
P |
= 2,5 KN |
|
N |
= 900 rpm |
|
m |
= 18 mPa*s |
|
p |
Mpa |
|
Te |
= 335°K |
Elenco dei simboli
|
P: carico sul cuscinetto |
Ra : rugosità superficiale |
|
N: vel. rotaz.in giri/min (rpm) |
m : viscosità lubrificante |
|
N': vel rotaz in giri/sec |
f : coeff. di attrito |
|
p: pressione media |
c : calore spec. Lubrificante |
|
L: lunghezza cuscinetto |
r : massa volumica lubrificante |
|
D: diametro cuscinetto |
Q : portata lubrif. all'inizio del meato in pressione |
|
C : gioco diametrale |
Qs: portata alimentazione lu 727f56h brificante |
|
S : n° di Sommerfeld |
Te: temperatura alimentazione lu 727f56h brificante |
|
h0 : altezza minima meato |
Tm : temperatura media lubrificante |
Svolgimento
Per il dimensionamento del cuscinetto si possono considerare :
- il rapporto L/D = 1, dal quale deriva che L = D ;
- il valore della pressione media ![]() , e quindi :
, e quindi : ![]()
la superficie su cui si ha il sostentamento, un rettangolo di lati L e D.
Utilizzando le relazioni precedenti e i dati del problema, si ha :
![]() ossia
ossia 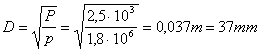
Quindi D = L = 37mm.
Poiché il cuscinetto in questione è del tipo poco caricato e lento, dal rapporto D/C = 1000 , si ha :
![]()
Si calcola anche :
![]()
Utilizzando i valori così ottenuti e quelli in possesso si ricava un numero adimensionale S, il numero di Sommerfeld:
![]()
che consente di ricavare gli altri parametri di funzionamento del cuscinetto utilizzando i diagrammi a disposizione.
Dal diagramma n° 1 si ricava infatti, per S = 0,15, il parametro adimensionale dal quale si ricava il valore di h0:
![]()
Onde evitare il contatto tra i due elementi
deve essere : ![]() .
.
Sostituendo il valore trovato si ha 7,4mm mm, quindi la relazione è verificata.
Dal diagramma n°2 si ricava, per S = 0,15, il
parametro adimensionale :![]()
dal quale si ha : 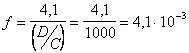
Dal diagramma n°3 si ricava un altro parametro
adimensionale ![]() dal quale si ha :
dal quale si ha :
![]()
Dal diagramma n°4 si ricava l'ultimo parametro
utile ![]() dal quale si ha :
dal quale si ha :
![]()
Utilizzando i parametri è stato possibile ricavare i valori dell'altezza minima del meato, del coefficiente di attrito, della portata del lubrificante all'inizio del meato in pressione
e della portata di alimentazione.
E' necessario a questo punto fare un bilancio
termico per il cuscinetto per valutare se il fluido, che entra nel sistema ad
una temperatura Te, ma durante il funzionamento si riscalda in
quanto assorbe il calore prodotto per attrito, mantiene oppure no le
caratteristiche richieste. In caso affermativo l'olio viene tenuto, in caso
negativo si sceglie un olio diverso e si calcolano i nuovi parametri
funzionali. Si ipotizza che tutto il calore prodotto dal cuscinetto venga
assorbito dal fluido e quindi, per la condizione di adiabaticità, si uguagliano
la potenza dissipata e il calore assorbito, ![]() dove la potenza
dissipata è :
dove la potenza
dissipata è :![]() e il calore assorbito è :
e il calore assorbito è : ![]() .
.
La temperatura media alla quale si porta
l'olio è Tm e si ricava dalla uguaglianza : ![]() ossia da
ossia da ![]() . Infatti è :
. Infatti è :
![]()
Il diagramma n°5 mette in relazione la temperatura (in °F) e la viscosità m del lubrificante.
Se non esiste, come in questo caso, nessun olio SAE con queste caratteristiche, si cerca l'olio caratteristico più vicino. Nel caso in esame è il SAE-30 che alla Tm = 150,8°F ha una viscosità mI = 24 mPa*S.
Il procedimento precedente viene ripetuto, per iterazione, fino ad ottenere un ciclo chiuso.
Per mI = 24 mPa*S si ha S I = 19 e dai diagrammi si ottengono i seguenti valori :
|
mI |
= 24 mPa*S |
|
ho I |
= 0,0104 mm |
|
f I |
|
|
Q I |
= 560 mm3/s |
|
Qs I |
= 322 mm3/s |
|
Tm I |
= 340°K = 67°C = 152°F |
A questa temperatura si trova un valore di mII = 22mPa*S; facendo di nuovo l'iterazione si ha :
|
mII |
= 22 mPa*S |
|
fII |
|
|
Q II |
= 560 mm3/s |
|
QsII |
= 330,4 mm3/s |
|
Tm II |
= 340,7°K = 67,7°K = °153°F |
Ma a questa temperatura si trova un valore di mIII = 22mPa*S, quindi si chiude qui l'iterazione e si può affermare che si può utilizzare un olio SAE-30 che nelle condizioni di equilibrio possiede le seguenti caratteristiche :
|
Tm |
= 340°K |
|
m |
= 22 mPa*S |
|
D |
= 40mm |
|
L |
= 40mm |
|
C |
= 0,04mm |
|
ho |
= 1,02*10-2 mm |
|
f |
|
|
Qs |
= 330,4 mm3/s |
|
Tm |
= 340°K |
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"FRENATURA"
Nell'impianto di montacarichi schematizzato in fig.1 la frenatura è ottenuta mediante un freno a ceppi flottanti equilibrato, del tipo di fig.2.
Supposto che la frenatura avvenga nell'intervallo di tempo tf con accelerazione costante, si determini, con i dati forniti, il valore della forza F necessaria per la frenatura.
Elenco dei simboli e dei dati :
|
P |
= 12,5 KN |
= peso del carico |
|
Rp |
= 0,20 m |
= raggio della puleggia |
|
v0 |
= 1,1 m/s |
= velocità di discesa iniziale |
|
tf |
= 0,2 s |
= tempo di frenatura |
|
Jp |
= 10 Kg*m2 |
= momento di inerzia ridotto all'asse della puleggia |
|
t |
|
= rapporto di trasmissione del riduttore |
|
h |
|
= rendimento di trasmissione del moto retrogrado |
|
a |
|
= angolo di abbracciamento dei ceppi |
|
f |
|
= coefficiente di attrito tra ceppi e tamburo |
|
Rf |
= 0,170 m |
= raggio del tamburo del freno |
|
a |
= 0,450 m |
= quota del freno |
|
b |
= 0,220 m |
= quota del freno |
|
c |
= 0,016 m |
= quota del freno |
|
d |
= 0,160 m |
= quota del freno |
Svolgimento
Poiché il moto durante la formatura è uniformemente ritardato, è possibile ricavare il valore dell'accelerazione visto che la velocità della discesa iniziale e il tempo tf di frenatura sono note. Essendo infatti : v = v0 - a* tf e anche v = 0 si ha :
![]()
Il momento motore Mm può essere valutato utilizzando le forze che agiscono a valle della puleggia, ossia :
- la forza peso P ;
- la forza di inerzia, Fi, diretta verso il basso (perché si oppone all'accelerazione a diretta verso l'alto) ;il suo valore si ricava dalla relazione Fi = m*a = P/g*a.
Si ha infatti :
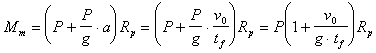
Il momento frenante rispetto all'asse 2 può essere valutato partendo dall'equazione di d'Alembert, nella quale si considera un momento di inerzia Jp ridotto all'asse della puleggia :
![]()
si integra :
![]()
si ricava Mf ricordando
che : ![]() ,:
,:
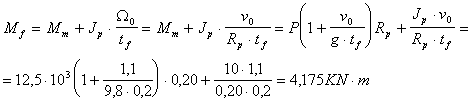
Si valuta il momento frenante all'asse 1, al
quale è applicato il freno, ricordando la definizione di rendimento nel moto
retrogrado: ![]() .
.
Ma ![]() , sarà perciò
, sarà perciò ![]() e quindi il momento
frenante è :
e quindi il momento
frenante è :
![]()
Si possono poi determinare le rette di azione delle forze che si trasmettono ceppo e tamburo. Queste devono contrastare la rotazione della puleggia che è oraria e di conseguenza sono dirette verso il basso. La risultante passerà per il punto B, nel quale è incernierato il ceppo flottante, e per un punto H che viene determinato graficamente dall'intersezione di una circonferenza di diametro ds (passante per l'asse del tamburo O e con il centro situato sulla bisettrice dell'angolo a) con una retta che passa per il punto di intersezione della circonferenza con l'asse BO e che forma con BO un angolo j
Con le seguenti relazioni si possono determinare ds e j
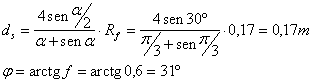
Per il punto H così trovato e per il punto B passa la retta d'azione della reazione cercata.
Facendo l'equilibrio sul primo ceppo si trovano le varie forze che agiscono sul ceppo. Si traccia una retta parallela alla retta trovata in precedenza e passante per la cerniera dell'altro ceppo, il punto D, si misura graficamente la distanza tra le due rette, si calcola il braccio della coppia di forze, si trova il valore L = 0,188m, quindi si determina il modulo di una delle due reazioni:
![]()
Facendo l'equilibrio per via grafica sulla leva di azionamento, si valuta la forza F da applicare nel punto G.
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"QUADRILATERO ARTICOLATO"
Al fine di trasformare un moto rotatorio continuo in un moto rotatorio alterno, si esegua il dimensionamento, con relativo disegno, di un quadrilatero articolato avente le seguenti caratteristiche:
b = 40° : angolo descritto dal bilanciere;
q = 15° : angolo differenza tra p e l'angolo descritto dalla manovella in una delle corse del bilanciere;
- O1O3 / O3B' = 1,1 : rapporto tra la distanza fra i centri di rotazione della manovella e del bilanciere (O1O3 ) e la lunghezza del bilanciere (presa a piacere).
Svolgimento
Preso O3B' = 8cm , si individuano i punti B' e B'' tramite l'angolo b e si ricava il raggio R che contiene i punti B', B'' e O1 usando la relazione:
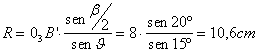
Si trova il punto O sulla bisettrice di b tracciando da B' un arco di raggio R. Essendo O1O3 / O3B' = 1,1 il segmento O1O3 = 8,8 cm, quindi si trova il punto O1 sulla circonferenza tracciando un arco di raggio O1O3 da O3 .
Si misurano le distanze O1B' e O1B'' e quindi si calcola la misura del raggio r della manovella usando la relazione :
![]()
E' possibile quindi disegnare il quadrilatero articolato.
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"FORZE NELLA GUIDA DI FAIRBARN"
Sia dato un meccanismo con glifo oscillante del tipo rappresentato in figura. Si calcoli, per il valore di q assegnato, il momento motore che occorre applicare alla manovella 1 nel caso che sul corsoio 5 agisca una forza resistente Q e supponendo che tutte le masse in gioco siano trascurabili rispetto a quella, m5, del corsoio 5.
Dati
|
q |
|
|
l3 / r |
|
|
l4 / r |
|
|
i/r |
|
|
d / r |
|
|
j |
|
|
m5 |
= 190Kg |
|
W |
= 30 rad/s |
|
Q |
=2500 N |
|
r |
= 2mm (sul disegno) |
Svolgimento
Si pone il raggio della manovella 1pari a 30 mm, si ricavano le grandezze caratteristiche dai dati del problema e si disegnano i vari schemi.
Per poter calcolare il momento motore da applicare alla manovella, è necessario ricavare il valore della forza di inerzia Fi della massa m5. Si calcola prima il valore dell'accelerazione aD che agisce sulla massa, poi facendo l'equilibrio tra i vari elementi si calcolano le diverse reazioni.
Si calcolano le velocità dei punti del glifo nella configurazione assegnata, considerandole a meno della velocità angolare W e ruotate di p/2 in senso antiorario.
Dallo schema 1 si vede che le varie velocità possono essere rappresentate come segmenti proporzionati, ricavabili graficamente nel modo seguente :
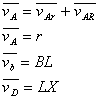
Tali segmenti moltiplicati per W danno il valore reale :
Si segue lo stesso procedimento per il calcolo delle accelerazioni dei vari punti del glifo, considerandoli però a meno di W e nelle direzioni giuste. Si ricavano così i segmenti proporzionati alle accelerazioni, i quali, moltiplicati per W forniscono i valori reali. Si ha allora :
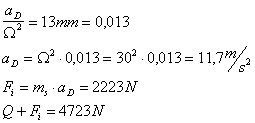
Dallo schema 3 si possono ricavare in modulo le diverse reazioni: infatti facendo graficamente l'equilibrio sui vari elementi e considerando l'attrito si ottengono i valori delle reazioni e le rette d'azione:
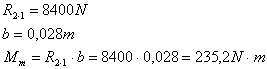
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"COSTRUZIONE DELL'EVOLVENTE DI CERCHIO"
Rappresentare, su foglio da disegno in scala 5 :1 secondo i dati assegnati, una porzione di ruota dentata. Si faccia riferimento ad una ruota normale con sporgenza uguale al modulo e rientranza uguale a 1,25 moduli. Si eseguano anche i raccordi dei profili ad evolvente dei denti con la circonferenza di piede.
Dati:
m = 4 mm : modulo
z = 18 : n° dei denti della ruota
n = 3 : n° dei denti rappresentati.
Con i dati assegnati calcolare poi il valore di W, dando conto dei calcoli eseguiti
Svolgimento
La misura Wilhaber permette di misurare lo spessore circolare s del dente e un semplice controllo delle tolleranze sullo spessore. Si misura la quota cordale W, pari alla corda che sottende un arco di circonferenza primitiva compreso tra i fianchi di due denti intervallati da un numero di vani tale che la corda, tangente al cerchio base, intersechi la primitiva nell'intorno dei fianchi considerati per la misura.
La misura Wilhaber si ricava, per denti diritti, dall'espressione:
![]()
dove pb = passo della ruota sulla circonferenza di base,
sb = spessore del dente sulla circonferenza base.
Nel caso in esame si ha :
![]() ( primitiva)
( primitiva)

dove s è lo spessore del dente calcolato sulla primitiva.
I valori sono dati per correzione nulla, quindi una ruota normale.
Si può scrivere :

Sostituendo i dati si ha :
![]()
Si calcola lo spessore del dente :
![]()
Infine si calcola :
![]()
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"CALCOLO DI UNA TRASMISSIONE A CINGHIE TRAPEZOIDALI"
Si debba trasmettere una potenza P mediante una trasmissione a cinghie trapezoidali. Il motore è elettrico a corrente alternata , a coppia normale (servizio normale: 8-10 ore al giorno). Sono noti i numeri di giri N e n delle pulegge minori e maggiori. Si scelgano: tipo, lunghezza, numero di cinghie, calcolando diametro delle pulegge, interasse, corsa per il montaggio e per il tenditore.
Dati
P = 6 CV
N = 1450 giri/min.
n = 480 giri/min.
Svolgimento
Si devono definire il numero, il tipo e la lunghezza delle cinghie da utilizzare e le dimensioni delle pulegge utilizzando i dati del motore e delle caratteristiche da trasmettere, nonché le condizioni di montaggio.
Tramite le caratteristiche di funzionamento e di utilizzo, si usa la tabella 1 per calcolare il coefficiente Cc = 1,2, necessario per il calcolo della potenza "corretta" da trasmettere :
![]()
Sul grafico n°1 si legge, in corrispondenza di questo valore di Pc e del numero di giri della puleggia minore (N = 1450 giri/min.), una indicazione di massima sulle dimensioni della puleggia piccola. Questi valori indicano una cinghia di tipo SPZ con un diametro tollerabile d = 63 100 mm
Poiché il rapporto teorico di trasmissione è ![]() si scelgono il
diametro maggiore e quello minore in modo tale che il rapporto reale sia vicino
il più possibile a quello teorico.
si scelgono il
diametro maggiore e quello minore in modo tale che il rapporto reale sia vicino
il più possibile a quello teorico.
Se si scelgono ad esempio i valori d = 67 mm e
D = 200 mm, il rapporto reale è ![]()
La velocità periferica sarà allora :
![]()
Si sceglie l'interasse tra le pulegge in modo tale che sia I D. Se I = 230 mm si calcola la lunghezza della cinghia :
![]()
Dalla tabella 3 si sceglie la lunghezza effettiva della cinghia disponibile, la SPZ 900, che ha una lunghezza di 900 mm.
Si calcola la lunghezza dell'interasse effettivo:
![]()
Si determina la potenza trasmissibile da una singola cinghia: Pt = Pb +Pd, dove Pb è la prestazione base e Pd quella differenziale. Dalla tabella 7 per interpolazione si ricavano i due valori : Pb = 1,44 CV e Pd = 0,3 CV, quindi si calcola la potenza trasmissibile:
Pt = Pb + Pd = 1,44 + 0,3 = 1,74 CV
La potenza attuale corretta Pa dovrà tenere conto sia dell'arco di contatto sia della lunghezza della cinghia, tramite i coefficienti C g e C.L.
Si calcola pertanto l'angolo di avvolgimento g
![]()
e si ricavano dalla tabella 5 il valore C g = 0,915 e dalla tabella 4 il valore C L = 0,88.
Si possono allora calcolare la potenza attuale
![]()
e il numero delle cinghie :
![]()
Si devono usare 6 cinghie SPZ 900.
Per il montaggio e per tendere la cinghia si usano i seguenti valori di corsa:
x = corsa tenditore = 0,03 L' = 27mm
y = corsa montaggio = 0,015 L' = 13,5 mm.
Nel disegno è schematizzata, in scala 1:2 , la trasmissione con le seguenti caratteristiche :
Tipo : SPZ 900
L' = 900 mm
D = 200 mm
d = 67 mm
Ie = 230,8 mm
x = 27 mm
y = 13,5 mm
z = 6
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"PROPORZIONAMENTO DI UN MECCANISMO A CAMMA"
Si consideri il cinematismo di azionamento della valvola di aspirazione di un motore per autoveicolo rappresentato in fig.1: la camma (1), ruotando con velocità angolare pari alla metà della velocità angolare dell'albero motore, comanda il bicchierino (2) che può supporsi solidale con la valvola (3).
Durante la fase di azionamento della valvola il contatto tra camma e bicchierino è assicurato dall'azione della molla (4). La stessa molla garantisce, a valvola chiusa, la tenuta sulla sede (5).
A valvola aperta, la posizione istantanea dell'equipaggio traslante è controllata dal contatto con la camma(1) ; a valvola chiusa la posizione dello stesso equipaggio è definita dal contatto con la sede (5); nel passaggio dalla configurazione di apertura a quella di chiusura (e viceversa) il contatto con l'equipaggio traslante si deve invece spostare dalla camma (1) alla sede (5).
Per assicurare un funzionamento corretto è quindi necessario garantire, a valvola chiusa, un seppur minimo gioco tra camma e bicchierino. Tale gioco può essere impostato a motore freddo (gioco nominale g), ma non può essere controllato e mantenuto rigorosamente costante durante il funzionamento. Per tale motivo il profilo della camma inizia e termina con rampe di recupero gioco, aventi la funzione di controllare l'entità degli inevitabili urti tra camma e bicchierino (all'inizio della fase di apertura della valvola), e tra valvola e sede (al termine della fase di chiusura della valvola) in corrispondenza di un determinato campo di possibili valori del gioco di funzionamento.
Detto q l'angolo di rotazione della camma, si richiede di determinare la legge del moto y = y(q) della valvola tenendo presenti i seguenti vincoli progettuali :
- legge di moto simmetrica rispetto alla configurazione di massima apertura ;
- alzata della valvola = h (al netto delle rampe di ripresa gioco) ;
- durata di azionamento della valvola corrispondente ad a gradi di rotazione dell'albero motore (al netto delle rampe di ripresa gioco) ;
- altezza delle rampe di ripresa gioco = h1 ;
- massima velocità d'urto = u ;
- massimo regime di rotazione del motore = n ;
- rampe di recupero gioco a velocità di impatto costante al variare del gioco di funzionamento ;
- tratto utile della legge di moto composto da tre archi polinomiali di ordine 5,4 e 5, raccordati tra loro a distanza q dalla configurazione di massima apertura ;
- continuità di y'''(q) (ossia di d3y / dq )in corrispondenza dei suddetti raccordi ;
- continuità di y''(q) in corrispondenza dei raccordi tra gli archi polinomiali di ordine 5 e le rampe di recupero gioco ;
- accelerazione della valvola nulla a distanza q dalla configurazione di massima apertura.
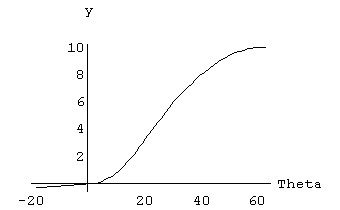
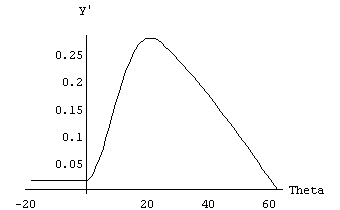
Si traccino gli andamenti di y e y' in funzione di q e di y'' sia in funzione di q che in funzione di y.
Si determini inoltre :
- il raggio base della camma in modo tale che il minimo raggio di curvatura del profilo sia pari a dmin.
- la forma della camma (se ne esegua il disegno in scala (2,5 :1) ;
- la massima distanza dall'asse valvola del contatto camma-bicchierino (l'asse dell'albero a camme e del bicchierino sono ortogonali e incidenti) ;
- il diametro minimo del bicchierino d, essendo pari a d/2 lo spessore della camma ;
- l'entità del precarico della molla a valvola chiusa e in condizioni di gioco nominale g= h1 ,affinché, in corrispondenza del massimo regime di rotazione del motore, la forza minima di contatto tra camma e bicchierino sia pari a F min. ; è nota la rigidezza K della molla e la massa m dell'equipaggio mobile della valvola.
Dati :
h = 10 mm
a = 252°
h1 = 0,3 mm
u = 270 mm/s
n(rpm) = 5400 rpm
q = 37°
q = 42°
dmin. 0,05 mm
Fmin. = 150 N
K = 10 N/mm
m = 0,220 Kg
DETERMINAZIONE DELLA LEGGE DEL MOTO
Assumiamo come origine degli assi nel piano (q, y) il punto di raccordo tra la prima rampa di ripresa gioco e il tratto di inizio di apertura della valvola. La legge del moto avrà un andamento come in fig.2. L'andamento del moto è simmetrico rispetto all'asse e-e , pertanto è sufficiente studiarne metà, ad esempio il tratto che va da P a S.
Nel sistema di riferimento (q, y) scelto, il punto S ha coordinate : S qs, ys)=(a ,h).
Per il punto P, è nota solo l'ordinata yp= -hp , mentre l'ascissa varierà al variare del gioco di funzionamento.
Il punto R avrà ascissa : qR a q e il punto Q avrà ascissa qQ a q
Il tratto PO corrisponde alla rampa di recupero gioco ed è definito dalla legge y0=y0(q) da determinare.
Il tratto OR è modellato da una legge polinomiale di 5° grado del tipo :
ya = a5q + a4q + a3q + a2q + a1q + a0.
Il tratto RS è un polinomio di 4° grado, simmetrico rispetto all'asse e-e, esprimibile mediante le potenze pari di (q - q s
yb = b4 (q q s) 4 + b2 (q - q s ) 2 + b0 .
I dati del problema sono sufficienti per individuare la rampa PO. Infatti misurando le rotazioni q in gradi e gli spostamenti della valvola in millimetri si ha :
![]()
In corrispondenza del massimo regime di rotazione del motore, è noto il rapporto:
![]()
e si ricava perciò:
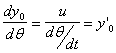
che è costante, per il vincolo progettuale di velocità di impatto costante.
Il tratto PO è rettilineo ed ha inizio
all'ascissa ![]() .
.
Si può procedere ora alla determinazione dei due punti di legge OR e RS, ossia alla determinazione dei nove coefficienti incogniti presenti nelle due polinomiali ya e yb .
Ricordando le condizioni richieste dal problema, le equazioni relative al raccordo delle rampe di recupero gioco con il tratto polinomiale di 5° grado sono le seguenti :
1) ya(0) = 0
2) y'a(0) = u / dq /dt
3) y''a(0) = 0
4) y''a (qQ
Per le condizioni richieste per il raccordo tra i due archi polinomiali di 4° e 5° grado si ha :
5) ya(qR) = yb(qR
6) y'a(qR) = y'b(qR
7) y''a(qR) = y''b(qR
8) y'''a(qR) = y'''b(qR
Infine la condizione sull'alzata massima della valvola corrisponde a :
9) yb(qb) = h
L'insieme delle relazioni scritte rappresenta un sistema di nove equazioni lineari nei coefficienti a0, a1, a2, a3, a4, a5, b4, b2, b0 .
Dalle equazioni 1), 2), 3) e 9) si ricavano :
a0 = 0
a1 = u / dq /dt
a2 = 0
b0 = h
L'individuazione delle rimanenti incognite a3, a4, a5, b4, b2 è subordinata alla soluzione del sistema delle altre cinque equazioni 4), 5), 6), 7),8).
Noti i coefficienti dei polinomi ya e yb, si tracciano gli andamenti di y(q), y'(q), y''(q) per i valori dell'angolo q compresi tra l'inizio della prima rampa e il termine dell'ultima; per i valori dell'angolo q appartenenti all'angolo complementare rispetto all'angolo giro si ha ovviamente y = -h1.
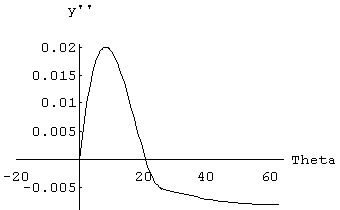
E' possibile tracciare il grafico di d2y/dt2 in funzione di y, tramite una tabella, nella quale sono affiancati i valori di q, y e y''.
Si traccia un grafico ponendo in ascissa i valori di y e in ordinata i valori di d2y/dq (y) ; per ciascuno dei valori di y presi ad intervalli regolari si cerca il valore di q sul grafico y = y(q) ; il valore di q così trovato consente di ottenere dal grafico della y'' = y''(q) il valore cercato che deve essere usato come ordinata del nuovo grafico.
DETERMINAZIONE DEL RAGGIO BASE DELLA CAMMA
Occorre esprimere il raggio di curvatura in un generico punto del profilo in funzione della legge di moto e del raggio base della camma.
La figura mostra la camma a contatto con il bicchierino nel punto E. Il centro di curvatura S del profilo della camma in E giace sulla normale n condotta per E al profilo stesso.
Detto O l'asse di rotazione della camma ed m la retta passante per O ed ortogonale alla direzione di movimento della valvola, il centro di istantanea rotazione C del moto relativo camma-bicchierino si trova nell'intersezione tra le rette n e m.
Poiché la superficie superiore del bicchierino è normale alla direzione di movimento della valvola, la lunghezza del segmento OC rappresenta la distanza della retta n dall'asse O.
A seguito di una rotazione infinitesima dq della camma, il punto del profilo a contatto con il bicchierino si sposta in E', il centro di istantanea rotazione diventa c' e la normale n' al profilo in E', passa per S e dista da O della quantità OC'.
Detta K l'intersezione di n ed m', il raggio di curvatura d = SE può essere espresso a meno di infinitesimi dello stesso ordine di dq, come : d = SK+CE.
Poiché C e C' sono i centri di istantanea rotazione, si può dire che :
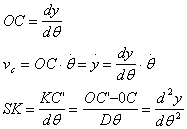
nelle quali q è espresso in radianti.
Detto R0 il raggio di base della camma si ha :
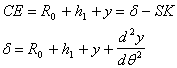
Il valore minimo di d, il dmin , è suggerito dal testo del problema ed
è relativo al punto del profilo della camma nella quale, essendo gli altri
termini di d costanti, è minima la quantità : ![]()
Per determinare il minimo valore di z, si procede analiticamente, sfruttando le espressioni di y e di d2y/dq , oppure graficamente tracciando nel diagramma (y,d2y/dq ) la retta r di equazione : y + d2y/dq
Si può individuare, nel fascio di rette parallele, una retta d che delimita inferiormente il grafico nella quale il valore dell'ordinata ON corrisponde al minimo valore di z cercato.
Sostituendo i valori trovati nella espressione di d, si trova il dmin dal quale si ricava R0 che sarà approssimato al decimo di mm.
TRACCIAMENTO DEL PROFILO DELLA CAMMA.
Si utilizza il metodo dell'inviluppo, oppure si traccia per punti il profilo della camma conoscendo, per ogni valore di q le lunghezze dei segmenti OC e CE, che si riportano in tabella. Le lunghezze dei segmenti si ottengono dalle espressioni :
OC = dy/dq
CE = R0 + h1+ y
DIAMETRO MASSIMO DEL BICCHIERINO (l)
Si ricerca in base alla massima distanza OCmax del contatto camma-bicchierino dall'asse della valvola, imponendo che il contatto si sviluppi sull'intero spessore della camma.
Deve quindi essere: ![]()
Poiché lo spessore della camma è dato pari a d/2, dovrà essere :
![]()
CALCOLO DEL PRECARICO DELLA MOLLA
La forza di contatto F tra la camma e il bicchierino è la seguente :
![]() ,
,
essendo :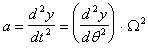
e T è il precarico della molla, ossia la forza con la quale la molla preme la valvola contro la sede.
L'accoppiamento camma-bicchierino è un accoppiamento di forza. L'equipaggio mobile segue effettivamente la legge di moto imposta dalla camma se, quando la valvola è sollevata dalla sede, la forza di contatto F è positiva o superiore ad un prefissato valore di Fmin. .
L'unico termine dell'espressione di F che può assumere valori negativi è quello iniziale. Esso contribuisce a deprimere F tanto più incisivamente quanto maggiore è la velocità angolare della camma. Vale infatti la seguente :
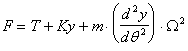
La determinazione della forza T deve essere effettuata in corrispondenza del massimo regime di rotazione del motore. Occorre quindi ricercare il valore minimo Wmin. della funzione :
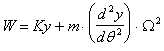
al variare di q. Come nel caso del raggio, il valore di Wmin. si può trovare graficamente come è stato fatto per zmin..
Noto Wmin. si trova il valore di Fmin. che, posto nell'espressione di F, ci dà T, l'incognita cercata.
Numericamente si procede nel seguente modo: si assume come origine degli assi nel piano ( q, y) il punto di raccordo tra la prima campa di recupero gioco e il tratto di apertura: il tratto PO starà sul semiasse negativo delle q
Per il tratto RO si ha :

E' il valore della ascissa di inizio della rampa di recupero.
Nel tratto OR, legge polinomiale di 5°grado :
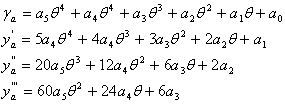
Nel tratto RS, legge di 4°grado polinomiale simmetrica :

Le nove condizioni per il calcolo dei nove coefficienti sono le seguenti :
1) ![]()
2) 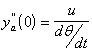
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
Si ricava così un sistema di nove equazioni in nove incognite che si utilizzano per ricavare le incognite a5, a4, a3, a2, a1, a0, b4, b2, b0 :
1) ![]()
2) 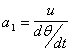
3) ![]()
4) ![]()
5) ![]()
6) ![]()
7) ![]()
8) ![]()
9) ![]()
Dalle equazioni 1, 2, 3, e 9 si ottengono quattro delle soluzioni cercate:
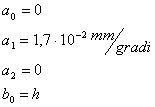
Tenendo conto che :
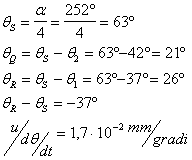
si mettono a sistema le altre cinque equazioni:

si sostituiscono i valori noti :
185220 a5 +5292 a4 +126 a3 = 0
11881376 a5 + 456976 a4 +17576 a3 +0,442= 1874161 b4 +1369 b2 +10
2284880 a5 +70304 a4 + 2028 a3 + 0,017 = -202612 b4 -74 b2
351520 a5 +8112 a4 +156 a3 = 16428 b4 +2 b2
40560 a5 +624 a4 + 6 a3 = -888 b4
e si risolve il sistema che fornisce le altre soluzioni cercate :
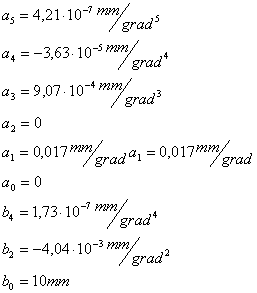
Si studiano le funzioni : y=y(q) ; y'=y'(q) ; y''=y''(q) ; y= y''(q
|
y = y(q |
y = -h |
|
|
|
y0 = a1q |
qP |
|
|
ya = a5q + a4q + a3q +a1q |
qR |
|
|
yb = b4 (q qS)4 + b2 (q qS)2 +b0 |
qR qS |
|
|
|
|
|
y'= y'(q |
y' = 0 |
|
|
|
y' = a1 |
qP |
|
|
ya' = 5a5q +4a4q +3a3q2 + a1 |
qR |
|
|
yb' = 4b4 (q qS)3 + 2b2 (q qS |
qR qS |
|
|
|
|
|
y''= y''(q |
y'' = 0 |
|
|
|
y'' = 0 |
qP |
|
|
ya'' = 20a5q +12a4q +6a3q |
qR |
|
|
yb'' = 12b4(q qS) 2 +2b2 |
qR qS |
|
|
|
|
![]() L'ultimo grafico
relativo alla d2y /dq in funzione di y, si ricava per punti, dalle funzioni y'(q) e y''(q
L'ultimo grafico
relativo alla d2y /dq in funzione di y, si ricava per punti, dalle funzioni y'(q) e y''(q
TABELLA DEI VALORI DELLE GRANDEZZE UTILI
PER LA COSTRUZIONE DEI GRAFICI
|
q grad |
y (q mm |
dy /dq mm/grad |
d2y /dq mm2/grad2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DETERMINAZIONE DEL RAGGIO BASE DELLA CAMMA.
Si applica la formula R0 dmin - h1 - z min per determinare il raggio base della camma.
Il valore di z min a cui
corrisponde il dmin si
ricava dal grafico n°4, tracciando la parallela alla retta di equazione ![]() , nel punto minimo del grafico.
, nel punto minimo del grafico.
Si ricava il seguente valore di z min = -13,13 mm, dal quale si ottiene :
R0 0,05 mm
TRACCIAMENTO DEL PROFILO DELLA CAMMA
Il tracciamento del profilo della camma è effettuato per inviluppo.
Si riporta lungo la semiretta che forma un angolo q con la direzione di riferimento, la distanza d = R0+h1+y(q) ed il segmento OC = dy / dq.
Si ricava il tracciamento riportato in fig. 3
DIMENSIONAMENTO DEL BICCHIERINO.
Il diametro si calcola valutando la massima distanza tra il punto di contatto della camma con il bicchierino e l'asse della valvola: si calcola il segmento OCmax e si verifica quanto segue :

la misura del diametro è d= 16,04 mm.
Si calcola il precarico della molla tenendo
conto che deve essere verificata la seguente relazione: Wmin Fmin - T ,nella quale Wmin deve essere calcolata
come il minimo della funzione :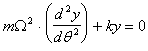 .
.
Per sostituzione si ottiene :
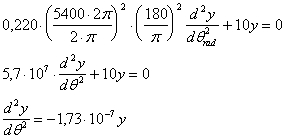
E' una retta molto prossima all'asse delle ascisse e quindi per approssimazione può essere ritenuta tale. Si verifica pertanto sul grafico d2y /dq , y il valore minimo :
Wmin = -0,00808 ( 180/p)2 = -26 N
e si può calcolare :
T Fmin - Wmin = 150 + 26 = 176 N
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
"CORREZIONE RUOTE DENTATE"
E' rappresentato in figura lo schema di un riduttore di velocità a ruote dentate cilindriche a denti diritti.
Sono noti i moduli e i numeri dei denti di tutte le ruote ; l'angolo di spinta di taglio è a 20° ; gli alberi di entrata e uscita devono essere rigorosamente coassiali ; l'interasse è quello nominale delle ruote 1 e 2.
Calcolare, con i dati riportati in tabella, l'angolo di spinta a' e la somma x3 + x4 delle correzioni delle ruote 3 e 4.
Dati
|
m1,2 |
= 4 mm |
|
m3,4 |
= 5 mm |
|
z1 |
|
|
z2 |
|
|
z3 |
|
|
z4 |
|
Svolgimento
Si calcola l'interasse nominale :
![]()
Si calcola l'interasse teorico in uscita :
![]()
Poiché gli interassi in ingresso e in uscita devono essere coassiali e l'interesse nominale deve essere a1,2 = a', si deve effettuare la correzione sulle ruote dentata 3 e 4 e la correzione risulterà sicuramente negativa.
Ricordando che a = a3,4 , si calcola l'angolo di spinta e di taglio a della relazione :
![]()
![]()
Si trovano le funzioni evolventi per entrambi gli angoli di spinta :
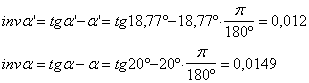
Utilizzando la relazione che mette le correzioni in funzione delle funzioni evolventi, si ricavano i valori delle correzioni da fare :
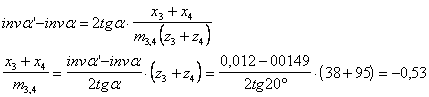
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
PARANCO ELETTRICO
Sia dato il paranco elettrico rappresentato nello schema allegato. Il carico sia sollevato da una puleggia mobile. In base ai dati forniti, si calcoli la potenza del motore, si scelga la fune, si determini il diametro del tamburo di avvolgimento e si esegua il dimensionamento cinematico del riduttore interposto tra motore e tamburo :
Dati
|
Q |
= 50 KN |
|
vS |
= 12 m/min. = 0,2 m/s |
|
nm |
= 700 rm |
|
h |
|
|
x |
|
|
i |
|
Elenco dei simboli
|
Q (KN) |
= carico da sollevare |
|
D (mm) |
= diametro del tamburo |
|
vS (m/min) |
= velocità di sollevamento |
|
nm (rm) |
= numero giri motore |
|
D (mm) |
= diametro della fune |
|
d (mm) |
= diametro dei fili della fune |
|
if |
= numero fili fune |
|
x |
= coefficiente sicurezza per funi in macchine sollevamento materiali |
|
PR (daN) |
= carico rottura minimo garantito dalla fune |
|
sR (daN/mm2) |
= tensione rottura minimo garantito dalla fune |
|
h |
= rendimento paranco |
|
t |
= rapporto di trasmissione del riduttore |
|
NM (KW) |
= potenza del motore |
|
zA, zB, zC, ecc. |
= n° denti per ruota |
|
i |
= n° dei satelliti |
Svolgimento
Si calcola la potenza motrice necessaria per sollevare il carico, utilizzando la relazione:
![]()
Si consulta la tabella che riporta i valori di potenza effettiva dei motori in commercio e si sceglie il motore che ha una potenza effettiva superiore o uguale a quella calcolata, ossia Nmeff = 12,5 KW.
Si sceglie la fune da utilizzare durante il sollevamento tenendo conto che si utilizza una puleggia mobile e che la fune è sottoposta ad un tiro pari a Q/2 (fig.1). Per semplicità di calcolo si considera la fune soggetta a un carico di sola trazione e si utilizza un coefficiente di sicurezza x molto elevato. Dovrà essere :
![]()
Si cerca, sulle apposite tabelle, la fune che verifichi questa e le altre quattro condizioni prescritte per il tipo di utilizzo (argano) :
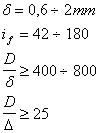
Tra le varie funi si sceglie quella che, a trazione maggiore, presenta un carico di rottura unitario, quella per la quale è sRmin = 160 daN/mm2 ; la fune che soddisfa queste condizioni è del tipo a cordatura normale, a trefoli, da 114 fili, del tipo 6x(1+6+12) con anima di tessuto, che possiede le seguenti caratteristiche:
Pr = 17000 daN ; D = 18 mm ; d = 120 mm.
Si possono calcolare così le dimensioni del tamburo :
D min D = 450 mm
D min d = 400 . 1,20 = 480 mm
Per comodità si sceglie un tamburo avente il diametro D = 480 mm = 0,480 m.
E' possibile ora ricavare il rapporto di trasmissione tra il motore e il tamburo.
Siccome si usa un motore che ha una potenza leggermente maggiore di quella calcolata, è opportuno verificare la nuova velocità di salita effettiva :
![]()
che risulta uguale a quella precedente.
La velocità periferica del tamburo è doppia rispetto a quella di salita (nell'ipotesi che il tamburo rotoli senza strisciare sulla fune), pertanto si possono calcolare la velocità angolare e il rapporto di trasmissione del riduttore:
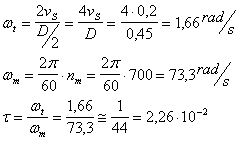
Il riduttore è diviso in due stadi e, per un buon proporzionamento, si assegna un t maggiore al primo stadio ; se t = 1/11, si può calcolare t
t = t t e quindi t t t = 1/4
Per dimensionare il riduttore è necessario calcolare il numero dei denti del pignone (A), del satellite (B) e della corona (C) sia del primo stadio che del secondo : zA, zB, zC, z'A, z'B, z'C.
Dalla formula di Willis : ![]() nella quale
nella quale
t = il rapporto di trasmissione del rotismo considerato ordinario
wn = la velocità angolare della n-sima ruota ( in questo caso : wn wc = 0 )
wp = la velocità angolare del portasatellite
w = la velocità angolare della ruota 1 ( in questo caso : w wA
si ricavano le seguenti :
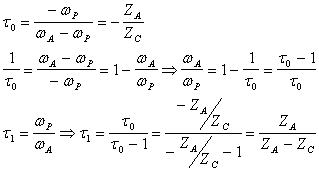
I diametri primitivi delle tre ruote (ruote normali, non corrette) sono legati dalla relazione : dC = dA + 2d B .
Poiché le tre ruote devono ingranare, dovrà essere :
m = d/z,
mzC = mzA + 2mz B
zC = zA + 2z B.
I satelliti ( i ) sono tre, disposti a 180° per poter equilibrare il sistema e quindi dovrà essere : zA + 2zC = c.i , nella quale c è un numero intero. Ciò vuol dire che zA e zC devono essere o entrambi positivi o entrambi negativi e la loro somma deve essere un multiplo di tre, del numero dei satelliti.
Si consideri il sistema :
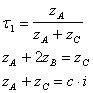
Se si indicano i rapporti di trasmissione tra
le ruote AB e BC per il primo stadio con : 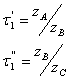
la formula di Willis diventa :
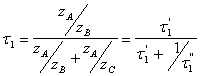
e dalla seconda equazione del sistema si ricava :
![]()
Mettendo a sistema le due equazioni :
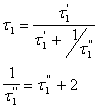
e facendo le opportune sostituzioni si ricavano :
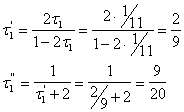
Si sceglie il valore di za superiore al minimo (17) e si ottiene
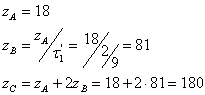
Si può allora verificare l'ingranamento :
![]()
che appare giusto.
Per il secondo stadio si procede in maniera analoga : dal sistema:
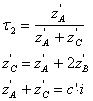
e dalla formula di Willis si ricavano :
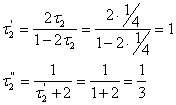
Per comodità si sceglie z'A = 18 e si calcolano :

Si procede alla verifica dell'ingranamento :
![]()
La verifica risulta positiva.
Il rotismo è così proporzionato :
|
1° stadio |
|
2° stadio |
|
z A = 18 |
|
z'A = 18 |
|
zB = 81 |
t |
z'B = 18 |
|
z C = 180 |
|
z'C = 54 |
|
t |
|
t |
Esercizio n
Esercitazione di Meccanica applicata alle Macchine
DENTATRICE STOZZATRICE
In figura 1 è assegnato lo schema cinematico di una dentatrice stozzatrice. Nota la frequenza di rotazione della manovella, supposta in prima approssimazione costante, tracciare per punti (almeno 12) i diagrammi del rapporto w w (velocità angolare bilanciere / vel. ang. manovella) e dell'accelerazione aS della slitta in funzione della corsa della slitta stessa e dell'angolo di manovella.
Si calcoli inoltre, in assenza di attrito, la forza risultante della forza di taglio T, della forza elastica della molla Fel e della forza d'inerzia Fi relativa al mandrino portautensile.
Si riporti l'andamento del momento resistente, applicato all'albero di manovella, in funzione di a, trascurando tutte le altre azioni d'inerzia e se ne faccia l'integrazione grafica, ottenendo l'andamento del lavoro resistente. Si determini quindi K, supponendo il momento motore costante.
Noti d e w si determini il momento d'inerzia totale. Supponendo poi che il momento
d'inerzia, ridotto all'albero della manovella, di tutte le masse del cinematismo sia, in prima approssimazione la metà di quello totalmente richiesto, si dimensioni e si disegni il volano.
Dati
|
a |
= 97,2 mm |
raggio di manovella |
|
b |
= 378 mm |
lunghezza biella |
|
c |
= 324 mm |
lunghezza asta quadrilatero |
|
d |
= 540 mm |
distanza centri di rotazione O1-O3 |
|
R |
= 162 mm |
raggio primitivo settore dentato |
|
n1 |
150 rpm |
numero giri manovella |
|
g |
|
|
|
mu |
= 30 Kg |
massa mandrino portautensile |
|
F0 |
= 400 N/mm |
forza elastica : Fel = F0 +F1* s |
|
F1 |
= 5 N/mm |
|
|
T |
= 4 KN |
forza di taglio |
|
d |
|
grado di irregolarità |
Svolgimento
Utilizzando lo schema cinematico di fig. 1 si consideri il quadrilatero O1ABO3 per la determinazione del rapporto w w . Per le convenzioni adottate, la vA è rappresentata, a meno di w , con il segmento O1A
. Essendo vB = vAB + vA, le prime due velocità si ricavano graficamente tracciando il prolungamento di BA (per vAB)e una retta parallela a BO3 passante per O1 (per vB) che intersecano nel punto S.
Essendo vA = w *a ; vB = w *c ; sarà :
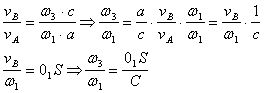
Si ricava questo rapporto per dodici diverse posizioni e si traccia il grafico richiesto.
Anche per determinare l'accelerazione della slitta si procede graficamente, con le convenzioni adottate (a meno di w ). Dal disegno si ricavano infatti le seguenti equazioni :
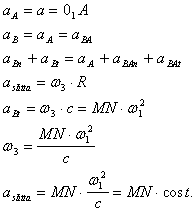
Graficamente sono stati trovati i valori di MN e di aS per diverse posizioni.
Nella fig. 2 sono rappresentati i punti considerati e i valori ricavati sono tabulati nella tabella finale. Per comodità, è stata considerata una rotazione della manovella in senso antiorario e sono stati ricavati i grafici di w w e di aS in funzione dell'angolo a di rotazione della manovella.
Presi i punti PMS e PMI della slitta, si ricava, in assenza di attrito, la risultante della forza di taglio T, della forza elastica F21 e della forza inerziale Fi relativa al mandrino portautensile. Si ottiene Fel = F0 + F1 *S dove S è lo spostamento della slitta e da questa si ha : Q = T + Fel + mu * aS
Dai risultati precedenti si ottengono i valori di Q, per le varie posizioni, ricordando che T è presente solo durante la fase di taglio. I risultati ottenuti sono tabulati :
Il momento resistente applicato alla manovella è ricavato in funzione di a
Poiché M3 = Q * R e devono essere verificate per ipotesi le condizioni:
![]()
si ricavano i valori di M3 e M1 che sono riportati in tabella.
In diagramma sono posti i valori di M in funzione di a
Integrando la curva ottenuta e ipotizzando il lavoro motore lineare, si ricava graficamente il lavoro eccedente K :
![]()
Si calcola il momento d'inerzia totale
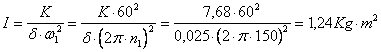
Si dimensiona il volano ricordando che il momento d'inerzia, ridotto all'albero della manovella, di tutte le masse del cinematismo deve essere per ipotesi approssimato alla metà di quello totale, ossia deve essere :
![]()
dove JC è il momento di inerzia della sola corona.
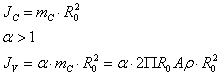
essendo ![]() dove b è un coefficiente di forma, ricavo :
dove b è un coefficiente di forma, ricavo :
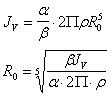
dalle tabelle scelgo b = 20 e a = 1,06, ipotizzo che sia di ghisa, quindi r = 7250 kg/m3, ottengo :
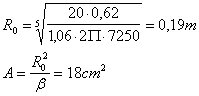
quindi ho :
b = 6 cm
h = 3 cm
|
Punti |
a [grad] |
yo [rad] |
w w |
s [mm] |
as [m/s2] |
T [N] |
|
PMI |
|
|
|
|
|
|
|
|
|
M/30 |
|
|
|
|
|
|
|
M/15 |
|
|
|
|
|
|
|
M/10 |
|
|
|
|
|
|
|
2M/15 |
|
|
|
|
|
|
|
M/6 |
|
|
|
|
|
PMS |
|
M/5 |
|
|
|
|
|
|
|
M/6 |
|
|
|
|
|
|
|
2M/15 |
|
|
|
|
|
|
|
M/10 |
|
|
|
|
|
|
|
M/15 |
|
|
|
|
|
|
|
M/30 |
|
|
|
|
|
Punti |
Fei [N] |
muas [N] |
Q [N] |
M3 [Nm] |
M1 [Nm] |
|
|
PMI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PMS |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026