|
|
| |
EVOLUZIONE GRANDEZZE FISICHE NELLO SCHEMA DI HEISENBERG
Nell'ambito delle trasformazioni unitarie assume particolare rilievo la traslazione temporale. Il generatore della traslazione temporale si deduce facilmente dalla soluzione formale dell'E 939d33j q. di Scrodinger.
![]() (1)
(1)
La (1) e' valida per operatori energia H indipendenti dal tempo. Dalla (1) otteniamo che il generatore della traslazione temporale e' proprio l'Hamiltoniana. Analogamente a quanto fatto per la traslazione spaziale e per le rotazioni possiamo esprimere gli elementi di matrice di un operatore su stati al tempo t come elementi di matrice di un operatore dipendente dal tempo su stati indipendenti dal tempo. Tale punto di vista in cui si preferisce associare l'evoluzione temporale alle grandezze fisiche e mantenere fissi nel tempo gli stati e' detto schema di Heisenberg.
![]() (2)
(2)
![]() (3)
(3)
Lo schema di Heisenberg e' interessante tutte le volte in cui si sa esplicitare la dipendenza dal tempo della grandezza di interesse. E' utile ottenere una equazione differenziale per gli operatori nello schema di Heisenberg. Se l'operatore non dipende esplicitamente dal tempo derivando rispetto al tempo si ha.
![]() (4)
(4)
Nella derivazione della (4) si e' fatto uso della invarianza di H
![]() (5)
(5)
Le proprieta' di commutazione si mantengono tra gli operatori trasformati
![]()
![]() (6)
(6)
Nel caso di una particella soggetta ad un campo di forze
![]() (7)
(7)
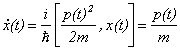 (8)
(8)
![]() (9)
(9)
Si noti l'analogia con le Eq. classiche del moto. Tale analogia porterebbe a pensare che nota una soluzione delle Eqs classiche tale soluzione e' anche una soluzione per l'evoluzione quantistica degli operatori. Questo e' vero solo se l'Energia potenziale e' una funzione al piu' quadratica in x>
![]() (10)
(10)
In questo caso possiamo esprimere la soluzione come una combinazione lineare con coefficienti dipendenti dal tempo degli operatori posizione e quantita' di moto al tempo iniziale.
![]() (11)
(11)
Sostituendo nella (8,9)
![]() (12)
(12)
![]() (13)
(13)
Le (12,13) definiscono insieme alle condizioni iniziali il moto armonico in presenza di una forza costante
![]()
Conviene trattare separatamente il caso c=0 ovvero sola forza costante e b=0 ovvero sola forza elastica.
Nel primo caso (c=0) dalle (13) e dalle condizioni iniziali si ottiene
![]()
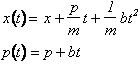
Riconosciamo il moto classico di una particella soggetta ad una forza forza costante in cui le condizioni iniziali sono sostituite dagli operatori posizione e quantità di moto nello schema di Scrodinger. Nel caso della sola forza elastica (b=0) riconosciamo l'equazione del moto armonico operando una seconda derivata nella (12)
![]() (14)
(14)
La soluzione è anche in questo caso il moto armonico classico espresso in termini della posizione e quantità di moto iniziale

Si noti che la dipendenza lineare degli operatori di Heisenberg da quelli di Scrodinger permette di esprimere il valor medio dei primi come una combinazione linere a coefficienti dipendenti dal tempo dei valor medi dei secondi
![]() (15)
(15)
I valori medi obbediscono peraltro alla legge di evoluzione delle grandezze classiche. Ciò era peraltro si poteva dedurre facendo la media delle equazione di evoluzione ( ).
![]()
Nel caso di una U(x) generale il moto del valor medio si può approssimare con quello classico solo se la media della forza si può approssimare con la forza calcolata nella posizione media.
Lo schema di Heisenberg è utile ogniqualvolta si è interessati al calcolo dell'evoluzione temporale di valori medi e non si richiede l'evoluzione dello stato.
HAMILTONIANA DIPENDENTE DAL TEMPO
Nel caso di un operatore energia che dipenda dal tempo l'operatore unitario che opera la trasformazione dello stato al tempo t=0 a quello al tempo t si ricava dalla Eq. di Scrodinger
![]() (16)
(16)
soddisfare la seguente Eq. di evoluzione
![]() (17)
(17)
Possiamo separare nell'operatore di trasformazione la parte connessa alla evoluzione con quella parte della Hamiltoniana H0 dove non compaiono i termini dipendenti dal tempo dalla parte dipendente dal tempo H1.Sostituendo nella (17) otteniamo

(18)
L' Hamiltoniana H1 si trasforma come si trasformerebbe un operatore nello schema di Heisenberg costruito con l'Hamiltoniana indipendente dal tempo. Tale particolare schema e' detto schema di interazione. Data la dipendenza dal tempo di H1 la (18) ha una soluzione sotto forma di serie.
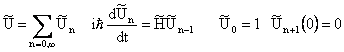 (19)
(19)
La soluzione della (19) si ottiene per iterazione.
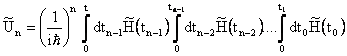 (20)
(20)
La (20) è una equazione complicata perchè in generale le hamiltoniane di perturbazione nello schema di interazione sono opertori dipendenti dal tempo che non commutano a tempi diversi.
L'Eq. (20) si semplifica drasticamente nel caso particolare in cui l'Hamiltoniana trasformata nello schema di interazione diventi indipendente dal tempo. Un esempio e' quello dell'oscillatore armonico soggetto ad una perturbazione del tipo
![]() (21)
(21)
In rappresentazione di interazione a ed a+ diventano
![]() (22)
(22)
La dipendenza temporale degli operatori di abbassamento ed innalzamento nella rappresentazione di interazione compensa l'oscillazione del campo esterno f(t).
![]() (23)
(23)
Sostituendo nella (20) e sfruttando la seguente identita'
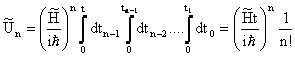 (24)
(24)
si ottiene un risultato che consente di sommare la (19)
![]()
Nel caso dell'oscillatore armonico forzato di (23) si ottiene
![]() (25)
(25)
Se infine lo stato iniziale e' lo stato fondamentale otteniamo uno stato coerente di ampiezza a(t) pari a
![]()
Si noti come l'ampiezza dell'oscillazione cresca linearmente nel tempo. Il sistema assorbe energia dalla perturbazione esterna.
Nel caso generale non sara' possibile risommare la (19) ma questa formula e' comunque utile per calcoli approssimati se nella H1 compare un parametro piccolo che consenta di troncare la serie ad un ordine finito.
Alternativamente il problema dell'oscillatore in presenza di una forza costante nello spazio e variabile nel tempo si può affrontare direttamente mostrando che se l'oscillatore è in uno stato coerente al tempo iniziale si mantiene in uno stato coerente sotto l'azione della forza con una ampiezza che varia nel tempo con la legge prevista dalla meccanica classica.
![]() (26)
(26)
![]() (27)
(27)
Nella (26) abbiamo espresso la condizione iniziale ovvero il carattere coerente dello stato al tempo zero. Nella (27) abbiamo espresso quello che vogliamo dimostrare: la coerenza al tempo t. La dimostrazione si ottiene applicando l'operatore di evoluzione ad ambo i membri della (26)
![]() (28)
(28)
l'operatore a(t) soddisfa l'equazione differenziale
![]() (29)
(29)
Esplicitando il commutatore otteniamo
![]() (31)
(31)
Nel caso particolare in considerazione l'equazione differenziale si può risolvere facilmente perché il termine dipendente dal tempo è il termine noto dell'equazione. La soluzione è la seguente
 (32)
(32)
Tornando alla (28) verifichiamo che se lo stato è coerente al tempo zero rimane coerente al passare del tempo con ampiezza
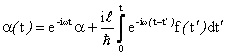 (33)
(33)
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025