|
|
| |
La superconduttività è una proprietà di molti metalli a bassa temperatura (dell'ordine di qualche grado Kelvin )scoperta da H.K. Onnes nel 1911 [Comm. Phys. Lab.,Univ. Leyden,119,120,122(1911)] quando con la liquefazione dell'Elio liquido divennero accessibili tali temperature. Recentemente ( Bednoz Mueller ...)la stessa proprietà si è ritrovata in alcuni composti ceramici a temperature molto più elevate (dell'ordine di grandezza della temperatura di liquefazione dell'azoto). La caratteristica principale è la drastica riduzione della resistenza elettrica e l'espulsione del campo magnetico (Effetto Meissner). I due fenomeni sono collegati e ce ne possiamo rendere conto considerando cosa succede in una solenoide costituito da un filo superconduttore quando si accende un campo mgnetico. L'accensione provoca una brusca variazione del flusso concatenato col solenoide e quindi un campo elettromotore impulsivo che a sua volta determina una variazione della quantità di moto delle cariche presenti nel filo ed in definitiva l'instaurarsi di una corrente. Tale corrente permane al cessare del campo elettromotore nell'ipotesi che il filo sia superconduttore. La sup 232h71c ercorrente determina l'esclusione del campo magnetico dall'interno del filo . La formalizzazione di tale ragionamento porta al seguente sviluppo.
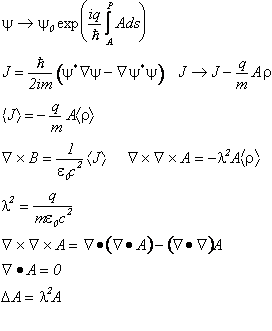
Nella penultima abbiamo approfittato dell'arbitrarietà della scelta di gauge.
L'ultima eq in prossimità della superficie de filo nella direzione normale si traduce all'equazione differenziale ordinaria.
![]()
La soluzione ci dice che il campo penetra nel filo solo per una distanza che è dell'ordine di grandezza della lunghezza di penetrazione l
L'ipotesi di una funzione d'onda macroscopica corrisponde alla teoria fenomenologica di London dei superfluidi. Il passo successivo fu di giustificare l'esistenza di uno stato macroscopico quantistico per un sistema di elettroni. Tale problema è stato risolto dalla teoria
Da queste considerazioni consegue che per spiegare la superconduttività occorre ipotizzare che al sistema di elettroni si possa associare un unico stato descritto da una funzione d'onda che in presenza di di un campo magnetico muti per un fattore di fase. L'ipotesi di una funzione d'onda macroscopica corrisponde alla teoria fenomenologica di London dei superfluidi. Il passo successivo fu di giustificare l'esistenza di uno stato macroscopico quantistico per un sistema di elettroni. Tale problema è stato risolto dalla teoria Bardeen Cooper Schieffer (BCS1957) per i metalli (Superconduttività a bassa temperatura) ma è tuttora irrisolto nel caso dei composti ceramici (superconduttori ad alta temperatura) .
La teoria BCS si basa sulla considerazione che lo stato fondamentale di un sistema di elettroni itineranti è instabile per una perturbazione associata ad una debole interazione attrattiva. L'instabilità porta ad uno stato fondamentale radicalmente diverso dallo stato fondamentale del sistema di elettroni itineranti.Ci proponiamo di illustrare nel seguito un possibile meccanismo per avere una interazione attrattiva ed una trattazione approssimata (del tutto equivalente alla teoria BCS anche se sviluppata in un modello leggermente diverso) che porta ad uno stato coerente macroscopico.
Il più semplice modello che considera le interazioni degli elettroni con le vibrazioni degli ioni del reticolo è il modello di Holstein(196..). Alla Hamiltoniana T degli elettroni itineranti si aggiungono, nel modello di Holstein, due termini: l'uno che descrive le oscillazioni reticolari come un insieme di oscillatori armonici indipendenti (per semplicità unidimensionali) ciascuno associato ad un sito reticolare ed un secondo che tiene conto della polarizzazione degli oscillatori armonici quando uno o due elettroni sono presenti sul sito.
![]() Eq.(1)
Eq.(1)
In Eq.(1) gli operatori a si riferiscono agli
oscillatori armonici, gli operatori ![]() danno il numero di occupazione
degli elettroni sul sito i. Come il precedente modello di Hubbard anche questo
modello non ha soluzioni esatte ma prevede una varietà di fenomeni che si
osservano in sistemi reali.
danno il numero di occupazione
degli elettroni sul sito i. Come il precedente modello di Hubbard anche questo
modello non ha soluzioni esatte ma prevede una varietà di fenomeni che si
osservano in sistemi reali.
In particolare ci serviremo del modello per studiare un nuovo caso di RSS che è la base per la comprensione della Superconduttività.
La simmetria in considerazione à la simmetria
sotto trasformazioni di Gauge dei gradi di libertà fermionici ![]() .
.
Per studiare questa nuova RSS procediamo come nel caso del modello di Hubbard. Se trascuriamo l"hopping" H diventa la somma di tanti termini ciascuno associato ad un sito e la funzione di partizione del sistema costituito da N siti indipendenti il prodotto di N termini identici ciascuno associato alla hamiltoniana di singolo sito. Questo limite è detto "limite atomico". Possiamo pertanto risolvere il problema relativamente ad un singolo sito. Eliminando l'indice di sito possiamo definire l'operatore K nel limite atomico.
![]() Eq.(2)
Eq.(2)
Riconosciamo in Eq.(3) un oscillatore armonico polarizzato con polarizzazionz proporzionale al numero di elettroni presenti sul sito. K si diagonalizza immediatamente con una trasformazione canonica di traslazione che opera sui gradi di libertà dell'oscillatore armonico in cui l'ampiezza della traslazione risulta dipendere dall'operatore numero di occupazione degli elettroni. Si ottiene così un operatore K' trasformato.
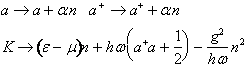 Eq.(3)
Eq.(3)
Riconosciamo in Eq.(4) la stessa struttura
del modello di Hubbard in cui però l'interazione tra gli elettroni nello stesso
sito U è negativa ![]() .Ciò si dimostra
facilmente osservando che per il principio di Pauli vale che
.Ciò si dimostra
facilmente osservando che per il principio di Pauli vale che ![]() e pertanto se K'è l'operatore K trasformato otteniamo
e pertanto se K'è l'operatore K trasformato otteniamo
![]() Eq.(4)
Eq.(4)
La diagonalizzazione ci ha portato a considerare dei nuovi gradi di libertà fermionici detti "polaroni" che sperimentano una interazione attrattiva se si trovano nello stesso sito. In altre parole l'energia diminuisce se se due elettroni si trovano nello stesso sito perchè aumenta la polarizzazione dell'oscillatore armonico associato al sito. La stessa diminuzione di energia si ottiene nella hamiltoniana trasformata per effetto di una interazione efficace attrattiva tra elettroni.
Gli autostati di K' sono il vuoto con autovalore nullo, lo stato singolarmente occupato con Spin "up" e lo stato singolarmente occupato con Spin "down" con autovalore -m, lo stato doppiamente occupato con Spin "up" e "down" con autovalore -2m+U. Per m=U/2 il vuoto e lo stato doppiamente occupato risultano essere degeneri in energia. Essendo U negativo gli stati singolarmente occupati risultano ad energia superiore. Lo stato fondamentale sarà pertanto una combinazione lineare dei due stati degeneri .
![]() Eq.(5)
Eq.(5)
Operatori che non commutano con la
trasformazione di Gauge ed il cui valor medio nello stato fondamentale di
Eq.(5) è diverso da zero sono gli operatori ![]() che rispettivamente
sottraggono e aggiungono una coppia di elettroni di Spin opposto al sistema.
che rispettivamente
sottraggono e aggiungono una coppia di elettroni di Spin opposto al sistema.
È pertanto naturale introdurre come perturbazione Hrs che elimina la degenerazione un operatore hermitiano costruito con una combinazione lineare di A e A+. Per semplicità assumiamo coefficenti eguali.
![]() Eq.(6)
Eq.(6)
Si noti che in questo caso non è possibile interpretare Hrs come l'interazione con un campo esterno fisicamente realizzabile.L'operatore A+A+ gioca in Hrs lo stesso ruolo dell'operatore magnetizzazione nel caso della RSS di tipo magnetico ed è pertanto naturale associare al valor medio di questo operatore il ruolo di parametro d'ordine per la RSS di tipo Gauge.In presenza della pertubazione di Eq.(6) lo stato fondamentale è la combinazione simmetrica del vuoto e dello stato doppiamente occupato con autovalore -l il primo stato eccitato è la combinazione antisimmetrica autovalore l. Su questi stati il valor medio di A+A+ è opposto. Gli stati singolarmente occupati rimangono autostati con lo stesso autovalore. In completa analogia con il caso magnetico è possibile calcolare il parametro d'ordine D, definito come media statistico-quantistica di A+A+,ottenendo che D risulta non nullo solo se prima si opera il limite di temperatura nulla e poi quello di perturbazione l che tende a zero.
Possiamo concludere dicendo che nel limite atomico si ha RSS di Gauge solo nello stato fondamentale (Temperatura nulla) e per m=U/2.
Per ottenere RSS di Gauge anche a temperatura non nulla per ottenere cioè un reale stato termodinamico occorre considerare l'effetto dell'"hopping".
Una prima difficoltà nasce dal fatto che l'operatore unitario che definisce la traslazione di Eq.(4), dipendendo dal numero di occupazione, non commuta con gli operatori di creazione e distruzione fermionici.
![]() Eq.(7)
Eq.(7)
![]() Eq.(8)
Eq.(8)
Ne consegue che il termine di "hopping" della Hamitoniana T degli elettroni itineranti si trasforma per effetto della traformazione unitaria di Eq.(7) nella somma di prodotti di operatori fermionici per esponenziali di operatori bosonici associati agli oscillatori armonici. In altre parole la trasformazione canonica non è in grado di diagonalizzare H (o K) quando si tiene conto dell'"hopping". Risulta utile introdurre l'approssimazione di sostituire ai suddetti operatori esponenziali il loro valor medio sullo stato fondamentale degli oscillatori armonici non polarizzati. Questa approssimazione (che si può giustificare nel caso in cui a sia molto maggior di uno) porta ad una ridefinizione dell'ampiezza t di "hopping". L'interpretazione fisica di tale ridefinizione di t è chiara nel modello che vede la trasformazione canonica come il passaggio da elettroni a "polaroni" intesi come complesso di elettrone e polarizzazione: i . polaroni hanno una minore ampiezza di probabilità di tunneling perchè devono trasferire da un sito all'altro anche la polarizzazione dell'oscillatore armonico.
Il passo successivo è quello di introdurre una nuova versione della approssimazione di Campo molecolare.
![]() Eq.(9)
Eq.(9)
In questa versione compaiono due parametri che saranno determinati nell'ambito del metodo variazionale l'uno è determinato dalla densità media e l'altro dalla media del parametro d'ordine. La modifica alla approssimazione di Campo molecolare di Eq.(9) si rende necessaria affinché l'approssimazione sia verificata almeno a livello atomico sullo stato fondamentale con RSS di Gauge di Eq.(5). Mediante Eq.(9) otteniamo una nuova Hamiltoniana detta Hamiltoniana di Campo molecolare.
![]() Eq.(10)
Eq.(10)
La grandezza s in (10) e nel seguito è una variabile dicotomica che indica lo stato di Spin "up" o "down" quando compare a pedice e corrispondentemente +1 o -1 quando compare a fattore. In Eq.(10) ns non dipende in realta da s non essendo presente un ordinamento magnetico. ns e D sono due costanti da determinarsi con un metodo variazionale del tutto analogo a quello illustrato nel caso magnetico.
Dalla condizione di minimo dell'Energia Libera
otteniamo che i parametri ![]() ,D coincidono con i
valori medi statistico-quantistici rispettivamente dell'operatore numero di
occupazione associato rispettivamente agli stati con Spin "up" e "down" e
dell'operatore che aggiunge (sottrae una coppia) di elettroni A+ (A)
definiti per ogni sito e mediati su tutti siti.
,D coincidono con i
valori medi statistico-quantistici rispettivamente dell'operatore numero di
occupazione associato rispettivamente agli stati con Spin "up" e "down" e
dell'operatore che aggiunge (sottrae una coppia) di elettroni A+ (A)
definiti per ogni sito e mediati su tutti siti.
![]() Eq.(11)
Eq.(11)
![]() Eq.(12)
Eq.(12)
Conviene notare che,in conseguenza delle regole di anticommutazione degli operatori fermionici, D non dipende in realtà dalla scelta di s. Per il calcolo di queste grandezze dobbiamo diagonalizzare l'Hamiltoniana di Campo Molecolare di Eq.10). Questa si diagonalizza con due passaggi successivi.
Passando al reticolo reciproco HCM diventa la somma di tanti termini indipendenti ciascuno associato ad un modo q.
![]() Eq.(13)
Eq.(13)
In Eq.(13) le energie eqs non dipendono da s per quanto già detto a proposito di ns. Gli operatori Aqs ed A+qs sono operatori che aggiungono o sottraggono una coppia di particelle in stati corrispondenti a modi q e Spin opposti.
![]() Eq.(15)
Eq.(15)
Il secondo passaggio consiste nella diagonalizzazione di Hq di Eq.(15). Questa si ottiene mediante la seguente trasformazione canonica.
![]()
![]() Eq.(16)
Eq.(16)
Eq.(16) è conseguenza della unitarietà della trasformazione canonica.Alla trasformazione di Eq.(16) è associato il seguente operatore unitario.
![]() Eq.(17)
Eq.(17)
L'Hamiltoniana trasformata assume forma diagonale per una particolare scelta dell'angolo qq associato alla trasformazione unitaria di Eq.(15).
![]()
 Eq.(18)
Eq.(18)
L'Hamiltoniana trasformata si esprime in termini di una nuova energia associata al vuoto di particelle E0 e delle nuove energie associate ai modi Eq .
![]() Eq.(19)
Eq.(19)
![]() Eq.(20)
Eq.(20)
Si noti che nella nuova energia dello stato fondamentale i termini che nascono dalla trasformazione canonica danno un contributo negativo in grado di compensare i termini positivi associati al campo medio (U è negativo) per dare un minimo a D diverso a zero. L'Energia Eq in H' ovvero l'energia dello stato con una particella nel modo q differisce da quella dello stato vuoto almeno di UD . Tale grandezza è detta "gap" di Energia ed è caratteristica dei Superconduttori.
È interessante determinare lo stato
fondamentale ![]() associato alla
Hamiltoniana H del nostro sistema valendosi dell'operatore Uq di Eq.(17) e
sapendo che l'Hamitoniana trasformata ha il vuoto di particelle come stato
fondamentale.
associato alla
Hamiltoniana H del nostro sistema valendosi dell'operatore Uq di Eq.(17) e
sapendo che l'Hamitoniana trasformata ha il vuoto di particelle come stato
fondamentale.
![]() Eq.(21)
Eq.(21)
Tale stato risulta essere una stato sovrapposizione di stati quantistici costituiti da vuoto , stati con una coppia di elettroni con Spin opposto appartenenti a modi q opposti, stati con due coppie con q diversi e così via.
![]() Eq.(22)
Eq.(22)
Il valor medio dell'operatore numero di particelle in tale stato risulta non nullo bensì dell'ordine del numero dei siti. Ovvero la densità ro delle particelle nello stato fondamentale si mantiene finita nel limite termodinamico.
![]() Eq.(23)
Eq.(23)
L'esistenza di uno stato fondamentale costituito da una sovrapposizione di stati di singola particella correlati è alla base del comportamento eccezionale noto come superconduttività. È chiaro che ciò modifica sostanzialmente le proprietà di conduzione del sistema. La resistenza di un comune conduttore si spiega facilmente ipotizzando un bilancio tra l'energia che gli elettroni ricevono dal campo elettromotore e quella che cedono all'ambiente. In ambedue i processi gli elettroni si considerano come indipendenti. La probabilità dei processi di cessione di energia diminuisce drasticamente quando lo stato fondamentale si trasforma da un prodotto di stati di elettrone singolo ad uno stato correlato quale quello di Eq.(21). I parametri D e n si determinano dalla condizione di minimo per la densità di energia libera.
![]() Eq.(24)
Eq.(24)
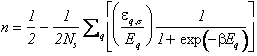 Eq.(25)
Eq.(25)
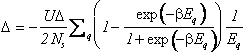
Si verifica facilmente che per m=U/2 n=1/2 (Condizione di semiriempimento).Introducendo infatti la densità degli stati la prima delle (25) si esprime come segue.

Per una densità degli stati simmetrica si verifica immediatamente che per m=U/2 n=1/2 è soluzione.
In questo caso si ottiena dalla seconda l'equazione di autoconsistenza per il secondo parametro variazionale associato alla RSS.
![]() Eq.(26)
Eq.(26)
Questa è un caso particolare (m=U/2) della celebre relazione ricavata per la prima volta da Bardeen Cooper e Schrieffer (1957) da cui l'acronimo di teoria BCS.La presente derivazione è diversa da quella originale che considera come punto di partenza l'instabilità di un gas di elettroni rispetto ad interazioni attrattive dovute all'interazione con i modi di oscillazione del reticolo cristallino.
La discussione della soluzione è del tutto simile a quella condotta per RSS magnetica. La soluzione simmetrica D=0 è stabile ad alta temperatura mentre a bassa temperatura si avranno soluzioni stabili con rottura spontanea di simmetria in corrispondenza delle soluzioni dell'equazione trascendente che si ottiene da (26)nell'ipotesi che D non sia nullo.
In particolare la temperatura critica è data dalla condizione seguente.
![]() Eq.(27)
Eq.(27)
Per l'occupazione media relativa al modo q otteniamo, tramite la trasformazione canonica, una espressione che ci permette di separare il contributo dello stato fondamentale da quello associato agli stati eccitati.
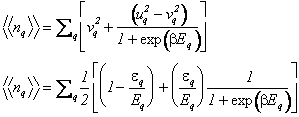
Notiamo che nella fase con RSS l'occupazione media di tutti i modi rimane diversa da zero nel limite di temperatura nulla. C'è una occupazione macroscopica dello stato fondamentale. Per le proprietà di trasporto in presenza di un campo magnetico conviene esprimere la densità di corrente media che si genera in presenza di un'anisotropia dell'hopping in una direzione del reticolo che assumiamo come direzione x .
![]() Eq.(27)
Eq.(27)
Utilizzando l'espressione dei numeri occupazione otteniamo
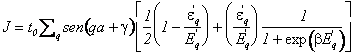 Eq.(28)
Eq.(28)
In Eq.(28) abbiamo indicato con un apice le grandezze che risultano modificate dalla presenza della anisotropia nell'hopping. In Eq.(28) il primo termine che rappresenta il contributo alla corrente associato allo stato fondamentale. Tale corrente è diversa da zero solo se si è in presenza di un campo trasverso e di una rottura di simmetria. È questa la corrente ipotizzata nella teoria fenomenologica di London. In Eq.(28) il primo termine rappresenta il contributo alla corrente associato allo stato fondamentale.
Per diminuire questa corrente è necessario sottrarre particelle allo stato fondamentale e portarle in stati di energia Èq superando la "gap" UD
Esiste anche una diversa possibilità per RSS di Gauge in cui il sistema si organizza ,nello stato fondamentale, in un ordine spaziale in cui in ogni direzione si alternano siti in media vuoti a siti in media doppiamente occupati. A tale ordine, detto di Onda di Densità di Carica, compete per m=U/2 la stessa energia libera dell'ordinamento superconduttivo mentre per m diverso da U/2 l'ordinamento supercondutivo ha Energia libera minore.Valgono i pregi e le limitazioni tipiche delle teorie di Campo molecolare già discusse nel caso magnetico. In particolare si ottiene una temperatura critica non nulla anche nel limite atomico in cui la densità degli stati diventa una delta di Dirac (N(e d e)) in contraddizione con il risultato esatto discusso precedentemente.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025