Probabilità , ampiezze di probabilià condizionate ed integrali sui cammini

_{Inserendo degli stati intermedi possiamo introdurre un Kernel di transizione associato alla probabilità condizionata all'osservazione della particella in n stati intermedi a tempi tn compresi tra} t₀ e t _K(x,t/x_n,t_n/x_n-1,t_n-1/...../x_1,t_1/x_0,t_{0). Possiamo generalizzare la ( ) nella}

  ₍₂₎

_{Vale la proprietà di Markoff}

₍₃₎

_{Iterando la ( ) si ottiene}

₍₄₎

Per ottenere il Kernel di transizione tra x,t e x_0,t₀ dobbiamo cercare una soluzione della Eq. di diffusione con la condizione iniziale.

  ₍₅₎

Questa è infatti la condizione perché la densità di probabilità definita al tempo t tramite il Kernel di transizione coincida per t che tende a t0 con la densità di probabilità definita al tempo t_0.

.NOTA...............

Al secondo membro della ( ) compare il simbolo della "delta" di Dirac. Si tratta di una distribuzione, di un concetto limite a cui si perviene considerando le proprietà di una famiglia di funzioni ogni elemento della quale è identificato da un parametro, la distribuzione si ottiene nel limite di tale parametro che tende a zero. Si consideri ad esempio la famiglia costituita dalle gaussiane centrate sull'origine e normalizzate di varianza s. Per s. che tende a zero l'ampiezza della la gaussiana diminuisce indefinitamente e contemporaneamente, dovendosi mantenere la normalizzazione, l'altezza nell'origine cresce indefinitamente. Si ottiene così la delta di Dirac una distribuzione che è ovunque zero tranne nell'origine in cui è infinito. Sono importanti le proprietà della delta di Dirac all'interno di un integrale.

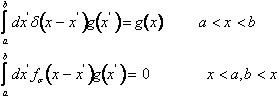₍₆₎

Possiamo dire cioè che la delta moltiplicata per una funzione ed integrata mi restituisce la funzione calcolata per il valore per cui è nullo l'argomento della delta se tale valore è all'interno dell'intervallo di integrazione altrimenti ottengo zero..

Tale proprietà si stabilisce facilmente partendo da una famiglia di funzioni dipendente da un parametro f_s x che associamo alla definizione della delta. Per tali funzioni noi assumiamo che siano definiti i momenti di ordine comunque elevato

(7)

e valga la seguente proprietà

(8)

Sfruttando le ( ) si può esprimere l'integrale tramite somma di momenti

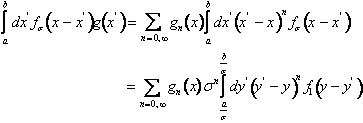(9)

Nel limite in cui il parametro s tende a zero nella somma sopravvive solo il momento d'ordine zero e ciò dimostra la proprietà della delta.

La soluzione dell'Eq. di diffusione che soddisfa la condizione iniziale è la soluzione gaussiana

    ₍₁₀₎

Utilizzando la ( ) per esprimere la probabilità condizionata ad n tempi si ottiene

₍₁₁₎

Scegliendo n sufficientemente grande si rende l'intervallo tra due tempi successivi piccolo. Scegliendo intervalli di tempo eguali t_n-t_n-1=t otteniamo che la densità di probabilità al tempo t si esprime come un integrale multiplo n-dimensionale. A ciascun punto dello spazio n-dimensionale possiamo associare un "cammino" una funzione del tempo q(s) continua e differenziabile per t₀<s<t con valori fissati agli estremi q(t₀)=x₀ q(t)=x. e agli istanti intermedi q(t_k)=x_k. Per intervalli di tempo sufficientemente piccoli possiamo approssimare l'esponente con un integrale. Possiamo riconoscere una grandezza nota in meccanica classica come Azione

(12)

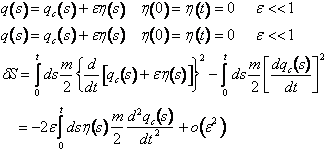
Nell'integrale multidimensionale la regione di maggior peso è quella in prossimità del cammino che rende minima l'azione. Tale regione di integrazione ha un peso tanto maggiore quanto più è piccolo il coefficiente di diffusione. Il cammino che rende minima l'azione si dice cammino più probabile. Per determinare tale cammino si calcola la variazione dell'azione rispetto al valore relativo ad un cammino prefissato q_c(s)

₍₁₃₎

Affinché la variazione sia nulla per qualsiasi scelta di h(s) il cammino di riferimento deve soddisfare l'equazione del moto rettilineo uniforme

    ₍₁₄₎

Le considerazioni precedenti si generalizzano immediatamente al caso dell'Eq. di Scrodinger sostituendo alla probabilita' condizionata l'ampiezza di probabilita' condizionata ed al coefficiente di diffusione D il corrispondente coefficiente quantistico. Si ottiene cosi'

   ₍₁₅₎

La regione di integrazione che dà il maggior contributo all'integrale sarà associata ai cammini per cui l'Azione varia poco, una variazione non piccola dell'azione porta infatti delle oscillazioni che sono molto molto fitte per la piccolezza della costante di Planck e quindi ad un contributo trascurabile all'integrale. Da queste considerazioni si conclude che anche nel caso delle Ampiezze di probabilitaà condizionate il cammino più probabile è quello che rende l'azione stazionaria.

La generalizzazione al caso di una particella che si muove in campo di forze si può fare proprio a partire da questa considerazione. Rimane infatti naturale sostituire l'azione associata al moto libero con quella associata al moto in un campo di forze.

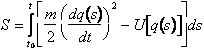
La condizione di stazionarietà individua come cammino più probabile il cammino classico. Ripetendo infatti le considerazioni precedenti otteniamo.

Dovendo la variazione essere nulla per qualsiasi scelta della perturbazione otteniamo l'equazione classica del moto.

Possiamo ora inferire quale sia l'equazione di evoluzione della ampiezza di probabilità ripercorrendo in senso inverso i passaggi che ci hanno portato dalla Eq; di evoluzione alla soluzione in termini di integrale sui cammini. La versione discreta della Azione sarà

Tale azione corrisponde ad una soluzione dell'Equazione di evoluzione per il'Kernel per tk<t<tk+1.

Ma questa è la soluzione dell'Eq

Tale soluzione deve valere per tempi prossimi a t_k  e per x prossimo a x_k. Possiamo facilmente generalizzarla per ogni tempo ed ogni x ponendo

Questa è l'Eq. di Schrodinger per una particella in moto in un campo di forze conservativo.

Conviene infine accennare che la formulazione in termini di integrali sui cammini si presta ad un prcedimento di approssimazione con cui si ottengono stati quantistici simili agli stati quasi classici dell'oscillatore armonico. Nel caso dell'oscillatore armonico è possibile calcolare l'integrale sui cammini ottenendo il Kernel di transizione degli stati quasiclassici.