"Teorema della Media"

matematica

"Teorema della Media"

Ipotesi: sia f(x) una funzione continua su [a,b] e positiva

Tesi: l'area (A) sottesa dalla funzione su [a,b] è uguale alla base (b-a) per una opportuna alte 828d36i zza f(c), cioè

A=(b-a)f(c)

dove c è un punto compreso in [a,b]

Dimostrazione: indichiamo ora con

m il minimo della funzione f(x) in [a,b],

M il massimo

n il numero di parti uguali in cui dividiamo [a,b]

h=(b-a)/n, la misura di ogni singolo intervallino

m_i il minimo della funzione f(x) su ogni intervallino, con i = 1,2,.,n

si ha evidentemente

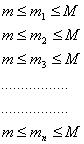
sommiamo ora i termini delle disequazioni precedenti

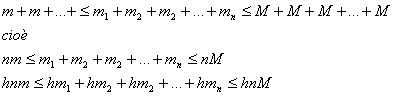
moltiplichiamo ora il tutto per h

sostituiamo ora h=(b-a)/n e semplifichiamo

(b-a)m< s_n  <(b-a)M (2)

applichiamo ora ai termini dalla (2) il limite per n tendente a più infinito, cioè

Il primo ed il terzo limite sono indipendenti da n, mentre il limite centrale per la (1) vale A

perciò

(b-a)m<A<(b-a)M.

Esiste quindi sicuramente un numero l, compreso tra m ed M tale per cui

A=(b-a)l. D'altra parte, essendo la funzione f(x) continua su [a,b],

esiste un numero c, in tale intervallo, tale che f(c)=l e quindi

A=(b-a)f(c) che è quanto volevamo dimostrare.