|
|
| |
![]() Si dice sistema di equazioni l'insieme di
due o pių equazioni nelle stesse variabili che sono verificate
contemporaneamente dai medesimi valori attribuiti alle incognite.
Si dice sistema di equazioni l'insieme di
due o pių equazioni nelle stesse variabili che sono verificate
contemporaneamente dai medesimi valori attribuiti alle incognite.
![]() Dato un sistema di due o pių equazioni in
altrettante incognite, si dice soluzione del sistema un insieme di valori delle
incognite che verificano contemporaneamente tutte le equazioni.
Dato un sistema di due o pių equazioni in
altrettante incognite, si dice soluzione del sistema un insieme di valori delle
incognite che verificano contemporaneamente tutte le equazioni.
![]() Un sistema di equazioni si dice intero se
tutte le equazioni se tutte le equazioni che lo costituiscono sono intere, si
dice fratto se almeno un'equazione č fratta.
Un sistema di equazioni si dice intero se
tutte le equazioni se tutte le equazioni che lo costituiscono sono intere, si
dice fratto se almeno un'equazione č fratta.
![]() Si dice grado di un sistema intero di
equazioni il prodotto dei gradi delle equazioni che costituiscono il sistema
Si dice grado di un sistema intero di
equazioni il prodotto dei gradi delle equazioni che costituiscono il sistema
![]() Si dice sistema numerico ogni sistema in
cui i coefficien 959c29j ti delle incognite sono tutti numeri, si dice letterale ogni
sistema di equazioni nelle quali uno o pių coefficienti contengono lettere.
Si dice sistema numerico ogni sistema in
cui i coefficien 959c29j ti delle incognite sono tutti numeri, si dice letterale ogni
sistema di equazioni nelle quali uno o pių coefficienti contengono lettere.
![]() Si dice che due sistemi di equazioni sono
equivalenti se tutte le soluzioni del primo sono anche soluzioni del secondo e
tutte le soluzioni secondo sono anche soluzioni del primo.
Si dice che due sistemi di equazioni sono
equivalenti se tutte le soluzioni del primo sono anche soluzioni del secondo e
tutte le soluzioni secondo sono anche soluzioni del primo.
![]() Un sistema
di equazioni che ammette un numero finito di soluzioni si dice determinato.
Un sistema
di equazioni che ammette un numero finito di soluzioni si dice determinato.
![]() Un
sistema di equazioni che ammette un numero infinito di soluzioni si dice
indeterminato.
Un
sistema di equazioni che ammette un numero infinito di soluzioni si dice
indeterminato.
![]() Un
sistema di equazioni che non ammette soluzioni si dice impossibile.
Un
sistema di equazioni che non ammette soluzioni si dice impossibile.
![]() PRIMO PRINCIPIO di EQUIVALENZA dei SISTEMI
PRIMO PRINCIPIO di EQUIVALENZA dei SISTEMI
![]() Se si sostituisce un'equazione di un
sistema con un'altra equivalente, si ottiene un sistema equivalente a quello
dato.
Se si sostituisce un'equazione di un
sistema con un'altra equivalente, si ottiene un sistema equivalente a quello
dato.
![]() SECONDO PRINCIPIO di EQUIVALNZA dei SISTEMI
SECONDO PRINCIPIO di EQUIVALNZA dei SISTEMI
![]() Se si ricava da un'equazione di un sistema
un'incognita in funzione di un'altra e si sostituisce l'espressione cosė
ottenuta, al posto dell'incognita, in un'altra equazione del sistema, si
ottiene un sistema equivalente a quello dato.
Se si ricava da un'equazione di un sistema
un'incognita in funzione di un'altra e si sostituisce l'espressione cosė
ottenuta, al posto dell'incognita, in un'altra equazione del sistema, si
ottiene un sistema equivalente a quello dato.
![]() TERZO PRINCIPIO di EQUIVALENZA dei SISTEMI
TERZO PRINCIPIO di EQUIVALENZA dei SISTEMI
![]() Dato un sistema di equazioni, si ottiene un
sistema equivalente a quello dato, se a un'equazione se ne sostituisce un'altra
ottenuta addizionando (o sottraendo) membro a membro le equazioni del sistema.
Dato un sistema di equazioni, si ottiene un
sistema equivalente a quello dato, se a un'equazione se ne sostituisce un'altra
ottenuta addizionando (o sottraendo) membro a membro le equazioni del sistema.
Teorema
![]() Determinata
Determinata![]() a/a'
≠ b/b'
a/a'
≠ b/b'![]() Indeterminata
Indeterminata![]() a/a'
= b/b' = c/c'
a/a'
= b/b' = c/c'![]() Impossibile
Impossibile![]() a/a'
= b/b' ≠ c/c'
a/a'
= b/b' ≠ c/c'
![]()
![]()
![]() ax
+ by = c
ax
+ by = c
a/a' b/b' c/c'
a'x + b'y = c
Metodo della sostituzione
![]()
![]()
![]()
![]()
![]()
x + y = 5 x = 5 - y x = 5 - y x = 5 - 3 x = 2
x - y = - 1 5 - y - y = -1 -2y = - 6 y = 3 y = 3
Metodo del confronto
5 - y = y - 1 -2y = -6 y = 3
![]()
![]()
![]()
![]()
x + y = 5 x = 5 - y x = 5 - 3 x = 2
x - y = - 1 x = y - 1 y = 3 y = 3
Metodo dei determinanti o regola di Cramer
![]() Si chiama matrice quadrata di ordine 2 una
tabella con 4 numeri disposti in linee orizzontali dette righe e in linee
verticali dette colonne
Si chiama matrice quadrata di ordine 2 una
tabella con 4 numeri disposti in linee orizzontali dette righe e in linee
verticali dette colonne
1° riga 2° riga
![]()
![]()
![]()
4
![]() M
M
![]()
![]()


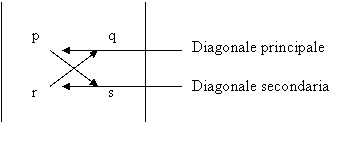
![]() Si
dice Determinante di una matrice quadrata di ordine 2 A = il numero ps - qr, ottenuto moltiplicando i
numeri della diagonale principale, e sottraendo da questo prodotto quello dei
numeri della diagonale secondaria.
Si
dice Determinante di una matrice quadrata di ordine 2 A = il numero ps - qr, ottenuto moltiplicando i
numeri della diagonale principale, e sottraendo da questo prodotto quello dei
numeri della diagonale secondaria.
D =
![]()
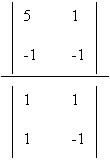
x + y = 5
x = Dx / D = = [-5 - (-1)] / [-1 - 1)] = - 4 / -2 = 2
x - y = - 1
![]()
x = 2
y = 3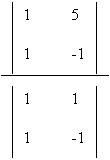
y = Dy / D = = (-1 - 5) / (-1 - 1) = -6 / -2 = 3
Metodo della riduzione
![]()
![]()
![]()
![]()
![]()
x + 3y = -1 3x + 9y = -3 x + 3y = -1 x -39/11 = -1 x = 28 / 11
![]() 0x + 11y = 13
0x + 11y = 13
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2026