Risoluzione delle disequazioni irrazionali - La forma di una disequazione irrazionale

Risolvere disequazioni irrazionali in generale non è difficile, anche perché noi ci limiteremo al caso più semplice degli esempi (1) e (2) che potremmo schematizzare in questo "tipo": , MA richiede un poco di pazienza e un poco di ragionamento.

2 - Elevare al quadrato entrambi i membri

Partiamo da un presupposto che spero risulti subito chiaro: in una disequazione non si può in generale elevare al quadrato e questo risulterà subito chiaro dal considerare un esempio numerico: se è vero, com'è vero, che 4>(-5), quando elevo al quadrato entrambi i membri NON è ovviamente vero che 16>25! Dunque si pone una prima importante limitazione alla nostra "libertà": possiamo elevare al quadrato entrambi i membri di una disequazione solo se sono positivi o nulli infatti se entrambi i membri sono positivi, anche al quadrato la disuguaglianza si mantiene, ovvero si ottiene una disequazione diversa dall'iniziale, però con lo stesso significato: se 3>2 anche 9>4, coi numeri tutto è semplice, ma con le lettere. Consideriamo la banale disequazione x>2, che ha soluzione S=]2,+∞[, se noi eleviamo al quadrato otteniamo la disequazione: x²>4 che invece ha soluzione: , che è ben diversa dalla disequazione iniziale, il fatto è che abbiamo elevato al quadrato senza preoccuparci del fatto che i due membri fossero positivi! Ovvero al secondo membro 2, che è un numero, è certamente non negativo, ma al primo membro x potrebbe essere anche negativa! Noi non sappiamo prima di risolvere la disequazione se x è positivo o negativo, però può essere solo una delle due cose, questo fatto che sembra banale in realtà ci sarà di grande aiuto per risolvere le disequazioni. Vediamo di ragionare intanto su questo piccolo esempio: se x fosse negativo la disequazione x>2 sarebbe ovviamente impossibile, infatti un numero negativo non può essere maggiore di 2. Dunque prima di procedere all'elevamento al quadrato dobbiamo supporre x positivo, d'altro lato, lo ripeto, x negativo è un non-senso. Se x è positivo possiamo allora elevare al quadrato e otteniamo la disequazione x²>4, con la soluzione sopra indicata, ma da questa soluzione noi dobbiamo togliere la parte che comprende valori negativi di x, cioè la soluzione finale si ottiene considerando i valori positivi dell'insieme che sono poi quegli stessi valori della disequazione x>2. Chiariremo meglio questo aspetto importante nel seguito, per ora limitiamoci a questa considerazione: in una disequazione NON posso elevare entrambi al quadrato, altrimenti rischio di creare dei non sensi come dedurre da 4>(-5) che 16>25. Però se entrambi i membri sono positivi posso elevare al quadrato, poiché in questo caso non creo nessuna contraddizione. Ma quando ho in mezzo delle incognite, delle quali non posso dire se sono positive o negative, che fare? Posso elevare al quadrato oppure no? Semplicemente faccio le uniche due ipotesi possibili: una quantità può essere positiva oppure non positiva, e punto, non è data alternativa. Se la suppongo positiva posso elevare al quadrato, se la suppongo non negativa NON posso, però in questo caso generalmente non ne ho bisogno!

3 - I radicali esistono?

Sappiamo che una radice quadrata produce un numero reale solo se il suo radicando è non negativo, per cui di questo dovremo tener conto quando risolviamo disequazioni irrazionali, questo è in realtà il primo dei presupposti: il radicando deve essere sempre posto ≥ 0 pena la "non esistenza" della radice . Quando il radicando è positivo noi consideriamo i radicali cosiddetti "aritmetici", dunque quando abbiamo un numero positivo sotto radice pensiamo ad un risultato pure positivo: e non anche -15, anche se (-15)² è pur sempre 225, tuttavia ci atteniamo alla definizione classica di radicale aritmetico per poter considerare funzioni le funzioni irrazionali , per questo possiamo concluderne che: un radicale quando esiste (ovvero con radicando non negativo) produce pure un risultato  ≥ 0. Questo ha importantissime conseguenze per la risoluzione delle disequazioni irrazionali. Come ho detto nel precedente paragrafo noi possiamo elevare al quadrato entrambi i membri di una disequazione solo se siamo assolutamente sicuri del fatto che sono positivi. Quando abbiamo delle disequazioni irrazionali elevare al quadrato ci potrebbe fare molto comodo, poiché una radice al quadrato produce come risultato il solo radicando (in valore assoluto, ma se noi abbiamo un radicando positivo, il suo valore assoluto coincide con il radicando), e dunque non ci sarebbero più radici di mezzo, e dunque potremmo risolvere la disequazione più facilmente. Abbiamo una forte limitazione sull'elevare al quadrato, ma adesso anche abbiamo un'informazione preziosa: che i radicali, supposta la loro esistenza, sono NON negativi, e quindi lì sappiamo che si può elevare al quadrato. Chiarisco con un esempio: il nostro esempio (1) , al secondo membro la quantità 1-6e è negativa, dunque so che non posso elevare al quadrato, d'altro lato non ne ho nemmeno bisogno, infatti ora so che il radicale del primo membro è, quando esiste, non negativo (cioè o positivo o nullo) ma un numero positivo (o tutt'al più nullo) non può certo essere minore di un numero negativo quale 1-6e. dunque questa disequazione è "impossibile", ovvero ha come insieme delle soluzioni l'insieme vuoto. Consideriamo ora il caso, solo leggermente più complicato, che in mezzo ci sia ">" invece di "<": consideriamo cioè la disequazione: , come abbiamo già osservato, al secondo membro c'è una quantità negativa, e dunque, ribadisco, non possiamo elevare al quadrato, ma di nuovo non ne abbiamo bisogno, infatti la quantità al primo membro è di sicuro, sempre che esista, positiva, o male che vada, nulla, quindi di sicuro è vero che il radicale del primo membro è maggiore del numero negativo che sta al secondo membro. Dunque diremmo la soluzione di questa disequazione è l'intero insieme dei numeri reali. MA ci dimenticheremmo di una cosa molto molto importante: che il radicale potrebbe anche non esistere, e in questo caso parlare di disequazioni non avrebbe proprio nemmeno senso. Dunque sì, la disequazione è sempre verificata purché il radicale al primo membro esista, ovvero purché il suo radicando sia positivo o nullo, ovvero ancora: la disequazione ha lo stesso insieme delle soluzioni di quella, decisamente più semplice: x+25≥0, e dunque S=]-25,+∞[, tutto qui! Così adesso puoi facilmente risolvere le disequazioni seguenti:

1) ,   2) , 3)

4 - I casi più complessi: positivo o no?

Riepiloghiamo le informazioni apprese in precedenza: si tratta di "principi guida", niente affatto nuovi, che ci aiuteranno a risolvere le disequazioni irrazionali, anche quelle più complicate:

E a questo punto consideriamo una disequazione "più classica", e cerchiamo di capire come si risolve:

Esempio 1 - .

Situazione: al primo membro un radicale, che quando esiste è positivo, dunque se fosse per il primo membro potrei elevare al quadrato anche subito. Al secondo membro invece una quantità, dipendente dall'incognita x, della quale non so se sia positiva o negativa. Dunque devo ragionare!

Schema logico della soluzione: se il secondo membro fosse negativo, allora la disequazione sarebbe impossibile, poiché il primo membro, che è positivo (sempre che esista!), o al limite zero, non può essere minore di un numero negativo. Dunque il secondo membro deve per forza essere positivo. Ma se deve per forza essere positivo, io posso elevare al quadrato! E dunque risolvo la disequazione con i seguenti passi: A) impongo alla radice di esistere, B) impongo al secondo membro di essere positivo, o eventualmente zero, C) elevo al quadrato. Poiché però questa terza fase C), l'elevamento al quadrato, è possibile solo se sono valide contemporaneamente anche le imposizioni A) e B), si tratta di sostituire alla disequazione irrazionale il seguente sistema risolvente:

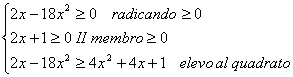
Questo è un sistema che non dà problemi di nessun tipo: la prima disequazione ha un'equazione associata con soluzioni 0 e 1/9, ed è risolta "per valori interni" (parabola rivolta verso il basso), la seconda è una disequazione di primo grado con soluzione S₂=]-1/2,+∞[, mentre la terza disequazione, raccogliendo i termini simili si riduce a: che non ha soluzioni reali, dunque il sistema non ha soluzioni, e dunque non li ha nemmeno la disequazione irrazionale: S è l'insieme vuoto.

Esempio 2

Situazione: al primo membro una quantità che potrebbe essere sia positiva che negativa (ma solo una delle due cose!), al secondo membro un radicale che esiste solo quando x è maggiore oppure uguale a -5. Non posso elevare al quadrato, poiché non so se la quantità al primo membro sia positiva o negativa.

Schema del ragionamento: il primo membro potrebbe essere negativo (quando x è minore di -1/2), in questo caso la disequazione sarebbe comunque sempre risolta nel caso in cui la radice esista, ovvero quando il radicando è non negativo. In questo caso, cioè, non possiamo elevare al quadrato, ma come sempre in questi casi, non ne abbiamo nemmeno bisogno! Il primo membro potrebbe d'altro lato essere anche positivo, in questo caso però potrei elevare tranquillamente al quadrato entrambi i membri. Il fatto è che nessuna ipotesi si può escludere, quindi devo risolvere due sistemi alternativi non esclusivi, ovvero devo risolvere un primo sistema corrispondente ad una prima ipotesi possibile, quella del primo membro negativo, poi un sistema corrispondente alla seconda ipotesi possibile, quella del primo membro positivo, quindi considerare l'unione delle due soluzioni. Soluzione: possiamo sostituire alla disequazione irrazionale l'unione delle soluzioni dei due sistemi seguenti: .

Le due ipotesi sul primo membro sono alternative e non esclusive, cioè: non sapendo io se il primo membro è positivo o negativo devo supporre che sia entrambe le cose e ragionare sulle conseguenze della mia ipotesi. Nel secondo sistema la condizione sul radicando è messa tra parentesi, infatti è inutile poiché è già contenuta nella terza disequazione dello stesso sistema: in questa terza disequazione sta scritto che il radicando (x+5) è maggiore oppure uguale di un quadrato di binomio, che è sempre positivo, quindi anche il radicando è positivo, quindi la seconda disequazione è inutile. Veniamo a calcolare le soluzioni: conviene distinguere tra primo sistema e secondo sistema, indicheremo con S_I le soluzioni del primo sistema (corrispondenti alla prima ipotesi possibile sul primo membro) ed S_II le soluzioni del secondo sistema, dopodiché l'insieme delle soluzioni S della disequazione irrazionale si otterrà dall'unione dei due insiemi S_I e S_II precedentemente trovati. All'interno dei singoli sistemi invece procederemo nel modo consueto, risolvendo separatamente le varie disequazioni, e intersecando successivamente gli insiemi delle soluzioni. Primo sistema: la prima disequazione è banalmente risolta per x<-1/2, la seconda per x≥-5, dunque: Secondo sistema: la prima disequazione è risolta per x≥-1/2, la seconda è compresa nella terza, la terza semplificando i termini simili si riduce a: 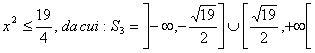ora si deve procedere all'intersezione di questa con la soluzione della prima disequazione del sistema, e dunque si ottiene: 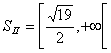. Soluzione finale del sistema: adesso basta unire le due soluzioni ottenute, si tratta cioè di incollare i due intervalli ottenuti in precedenza, dunque in definitiva la soluzione sarà: .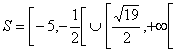

5 - Risolvere disequazioni irrazionali dentro a un dominio

I due esempi precedenti riassumono i due tipi fondamentali di disequazioni irrazionali nelle quali ci si può imbattere. Si può però procedere in un modo leggermente diverso in ogni caso, se noi partiamo dalla premessa che ogni radicando deve essere non negativo, e risolviamo intanto quella disequazione, individuiamo il dominio entro il quale selezionare le soluzioni accettabili della disequazione, quindi possiamo dare uno schema ancora più generale di soluzione di una disequazione irrazionale (nei casi più complessi, ovviamente): si determina intanto un insieme D, dominio del radicale, poi si determinano i due insiemi S_I e S_II corrispondenti alle due ipotesi possibili sul membro non contenente il radicale (alcune volte una o tutte e due le ipotesi non si fanno, o perché impossibili, o perché il membro contiene un numero o una quantità certamente positiva o certamente negativa), infine si trova la soluzione finale S come intersezione tra D e l'unione di S_I e S_II, in formule: . Il metodo di individuare prima il dominio e poi risolvere la disequazione irrazionale distinguendo le due ipotesi possibile è molto conveniente quando si devono risolvere disequazioni fratte o sistemi di disequazioni contenenti radicali, e comunque rappresenta una "strada obbligata" quando si studia una funzione, poiché nello studio di una funzione partiamo proprio dalla determinazione del dominio, e dunque le varie considerazioni sulla "necessità di avere un radicando positivo", sono già state prese in considerazione. Utilizzando questo metodo studiamo la seguente disequazione:

Esempio 3 - risolvere la disequazione: .

Schema del ragionamento: fatta l'ipotesi che il radicando sia positivo, ovvero che il radicale al secondo membro esista, veniamo a ragionare sul primo membro, se questo fosse negativo avrei comunque una disequazione sempre vera all'interno del dominio, poiché un radicale (che è sempre maggiore o uguale a zero) sarà certamente maggiore di una quantità supposta negativa. Se il primo membro fosse invece positivo potrei elevare entrambi i membri al quadrato e risolvere di conseguenza una semplice disequazione di secondo grado.

Soluzione: determino il dominio, deve essere:

(il denominatore è un quadrato, dunque possiamo anche non considerarlo, questa soluzione si poteva trovare anche per via intuitiva: la differenza di 1 meno 1/ è positiva se 1/ è minore di uno, e questo accade quando il denominatore è maggiore di uno, ovvero bisogna che il quadrato di x sia maggiore di ¼, poiché 4 per ¼ è 1.).

Veniamo alle due ipotesi possibili sul primo membro. Prima ipotesi: se il primo membro è negativo la disequazione è sempre vera nel dominio (ma del dominio adesso ci preoccuperemo solo alla fine intersecando con D), quindi: 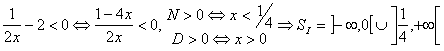. Seconda ipotesi: se il primo membro è positivo posso elevare al quadrato, dunque risolvo il seguente sistema di disequazioni razionali: 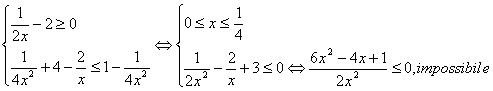infatti il numeratore della seconda disequazione ha un delta negativo, quindi il trinomio è sempre positivo, quindi non può mai essere negativo. Allora la soluzione definitiva della disequazione si ottiene intersecando D con S_I, e quindi: .

Concludo con l'esempio di una funzione:

Esempio 4: trova dominio ed insieme di positività della funzione .

Soluzione: partiamo dalla determinazione del dominio, i problemi sono: due radicandi e un denominatore, da cui il sistema: 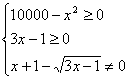la prima disequazione è di secondo grado, dunque procediamo alla solita maniera trovando le soluzioni per x che sono -100 e +100, poi disegnando la parabola ("verso il basso") infine interpretando le soluzioni, si tratta di valori interni, e quindi S₁=[-100,+100]. La seconda disequazione è una banale disequazione di primo grado, e quindi S₂=[1/3,+∞[, mentre la terza relazione comporta un ragionamento simile a quello che abbiamo fatto per risolvere disequazioni irrazionali: portiamo la radice al secondo membro, e abbiamo se il primo membro fosse negativo la disuguaglianza sarebbe sempre vera (un numero negativo è certamente diverso da un numero non negativo), per cui si può senz'altro supporre che il primo membro sia non negativo e quindi possiamo elevare al quadrato, otteniamo , quindi perveniamo al dominio intersecando le tre soluzioni: .

Veniamo alla positività, dobbiamo risolvere una disequazione fratta: nel dominio il numeratore è sempre positivo, infatti è la somma di due quantità positive, dunque la disequazione si riduce a quella del solo denominatore, che potremo scrivere così: . Ragioniamo al solito modo: il primo membro potrebbe essere negativo, ma questo comporterebbe l'assurdo di avere un numero negativo supposto maggiore di una quantità positiva o nulla. Quindi dobbiamo supporre che il primo membro sia positivo, e in questo caso possiamo elevare al quadrato e ottenere la disequazione di secondo grado: x²-x+2>0, l'equazione associata ha soluzioni x=-1,2, la disequazione è allora risolta nell'insieme , ma per determinare l'insieme di positività dobbiamo ora intersecare questo insieme col dominio, otteniamo così: S+=]2,+∞[.

ESERCIZI PROPOSTI

---