Permutazioni semplici P_n=D_n,n=n !

elementi ripetuti

Combinazioni semplici    diff. Per un elemento

con ripetizione

 

Stifel  ricorrenza

   

Limiti

Per il calcolo dei limiti ( x tende ad un numero finito o  all'infinito ), si utilizzano le formule seguenti quando sono noti i limiti finiti l e m. Noti: lim f(x)=l e lim g(x) = m

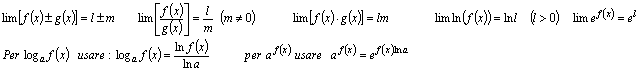
Nei casi esclusi dalle regole precedenti o per limiti infiniti si possono applicare le seguenti relazioni formali.

Somma:

Prodotto: Vale la regola dei segni.

Quoziente:

Esponenziale: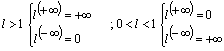    

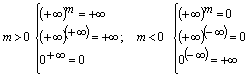
Logaritmo: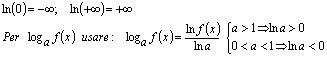

Limiti notevoli

Forme indeterminate

si applica la formula di De L'Hopital

Per le funzioni razionali fratte con

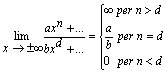
3) Si riconduce al caso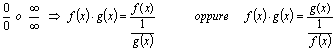

Si trasforma usando

Si riporta ad uno dei precedenti casi:

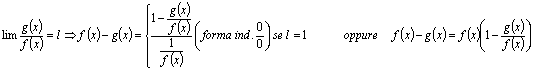
Se ci sono radicali si può razionalizzare: si moltiplica e si divide per lo stesso fattore, che elimina la differenza (o somma) fra radicali; ad es. se la funzione è del tipo , si moltiplica e si divide per

Derivate

Dc = 0

Funzione potenza

D x = 1

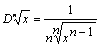
Funzioni goniometriche

D senx = cosx D cosx = -senx

Funzione logaritmica

 

Funzione esponenziale

D a^x = a^x ln a D e^x = e^x

Inverse delle funzioni goniometriche

 

Funzioni iperboliche

D shx = chx D chx = shx

Regole di derivazione

D kf(x) = kf'(x9  D [f(x) + g(x)] = f'(x) + g'(x) D [f(x) g(x)] = f'(x) g(x) + g'(x) f(x)

D f[g(x)] = f'[g(x)] g'(x)

 

Studio di funzione

Affinché una funzione y = f(x) sia continua nel punto x = c devono verificarsi contemporaneamente le seguenti condizioni:

esistenza del valore della funzione per x = c;

esistenza del limite finito l della funzione per x c (cioè );

coincidenza tra l e f(c).

Quando anche una sola delle tre condizioni non è verificata si dice che la funzione è discontinua e che x = c è un punto di discontinuità per la funzione (o anche punto singolare).

Punti di discontinuità di prima specie

Si dice che per x=c la funzione y = f(x) ha un punto di discontinuità di prima specie, quando esistono e sono finiti e diversi tra loro i limiti dalla destra e dalla sinistra della funzione, a prescindere dall'eventuale valore della f(x) per x = c

Punti di discontinuità di seconda specie

Si dice che per x=c la funzione y = f(x) ha un punto di discontinuità di seconda specie, quando non esiste, o non esiste finito, uno almeno dei due limiti dalla destra o dalla sinistra di c.

Punti di discontinuità di terza specie

Si dice che per x=c la funzione y = f(x) ha un punto di discontinuità di terza specie o eliminabile, quando esiste finito, il limite per x c di f(x), ma f(c) o non esiste o è diversa dal valore del limite.

Grafico probabile di una funzione

a)   determinare il dominio individuando dove f è continua

b)   determinare le eventuali intersezioni del suo grafico con gli assi coordinati

c)   studiare il segno della funzione individuando l'insieme di positività e negatività

d)   calcolare i limiti della funzione per x e in corrispondenza ai suoi punti di discontinuità, deducendo gli eventuali asintoti orizzontali e verticali

e)   tracciare, tenendo conto degli elementi acquisiti, il grafico probabile della funzione.

	Per ricercare tutti i flessi anche quelli a tg. Obliqua (condizione necessaria non sufficiente) ordine dispari ordine pari 0 fl. obliq. ne min. ne max. ne flessi. la curva volge la concavità verso l'alto  > 0 la curva volge la concavità verso il basso < 0

Flessi a tg. orizzontale

Ricerco la 1^a derivata

f'(x_i) > 0 funz.crescente f''(x_i) > 0 concavità verso l'alto

f'(x_i) < 0 funz decrescente    f''(x_i) < 0 concavità verso il basso

per trovare i flessi si pone f''(x) = 0 , si studia il segno di f''(x) nell'intorno dei valori trovati, se f''(x) cambia segno tra destra e sinistra del punto considerato si ha un flesso altrimenti no.

Se si ha un max o un min a tg orizzontale f'(x₀) = 0

Condizione necessaria, non sufficiente, affinchè vi sia un flesso in x₀ è che f''(x₀)=0

Per trovare i flessi perciò si deve porre f''(x)=0

Si studia quindi il segno della f''(x) nell'intorno dei valori trovati

Se f''(x) cambia di segno a destra e a sinistra del punto considerato si ha un flesso altrimenti no.

Se f'(x₀) > 0 funzione crescente in x₀   Se f''(x₀) > 0 concavità verso l'alto

Se f'(x₀) < 0 funzione decrescente in x₀ Se f''(x₀) < 0 concavità verso il basso

Massimi e minimi: se si ha un massimo o minimo relativo a tangente orizzontale f'(x₀) = 0

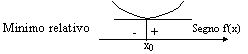
Tabella delle primitive

Formula di Archimede per l'area di un segmento parabolico