PROBLEMI DI SCELTA TRA DUE ALTERNATIVE

matematica

PROBLEMI DI SCELTA TRA DUE ALTERNATIVE

Teoria a pagina 60

Si tratta di problemi di scelta in situazioni di certezza con effetti immediati di massimo di minimo.

Si tratta in questo caso di scegliere in base al valore che potrà assumere la variabile tra due o più alternative.

Le alternative si evidenziano attraverso l'uso di più funzioni obbiettivo.

Il problema viene risolto graficamente, facendo nello stesso piano il grafico delle funzioni obbiettivo.

I punti di incontro fra le funzioni obbiettivo sono chiamati PUNTI DI INDIFFERENZA in quanto per i valori di x corrispondenti due alternative sono equivalenti.

Nei punti in cui le funzioni non sono equivalenti la scelta viene effettuata considerando i grafici; se il problema è di minimo viene scelta la alternativa rappresentata dalla funzione al di sotto, se è un problema di massimo la funzione sopra.

PROBLEMA

Una ditta produce un certo bene confezionato che deve conservare nei magazzini.

Si rivolge a due società che si occupano di stoccaggio e che propongono le seguenti alternative:

a)  euro 0,10 per ogni confezione e una spesa fissa settimanale di euro 25

b)  euro 0,50 per confezione fino a 40 confezioni e 0,25 euro per confezione eccedente le prime 40.

Determinare la tariffa più conveniente in base alla quantità da stoccare.

Situazione di certezza con effetti immediati di minimo con una variabile d'azione.

X è la variabile d'azione e può assumere valori positivi.

Y è il costo e deve essere minimizzato.

Le due alternative si rappresentano in due funzioni:

y =  0,10x +25

y = 0.5x

y = (0.50*40) + 0.,25 * (x-40)   x>40

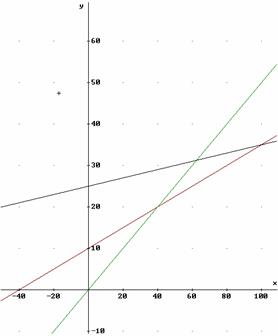y = 10 + 0,25x

PROBLEMA

Una ditta deve acquistare una fotocopiatrice e può scegliere tra due modelli

a)  costo iniziale di euro 2500 e un costo di euro 0.03 a fotocopia e un costo di manutenzione settimanale pari allo 0,5% del quadrato delle fotocopie eseguite

b)  comporta un costo iniziale di euro 1250 costo di 0,02 per fotocopia e un costo di manutenzione settimanale pari al 1,5% del quadrato delle fotocopie eseguite.

Determinare la scelta più conveniente in base al numero delle fotocopie.

Situazione di certezza con effetti immediati di minimo con una variabile d'azione.

X è la variabile d'azione e può assumere valori positivi.

Y è il costo e deve essere minimizzato.

Le due alternative si rappresentano in due funzioni:

a)  2500+ 0,03x +((x² *0.5)/100)

b)  1250+ 0,02x +( (x² *1,5)/100)

Esercizio n. 66 pagina 115

Per produrre una certa qualità di birra si possono utilizzare tre diversi impianti, i cui costi variano secondo la quantità in litri prodotta:

A: C(x) = 0.9x +300

B: C(x) = 0.75x+600

C: C(x) = 0.6x+1200

Determinare la scelta che permette la minor spesa in funzione dei litri di birra prodotti.

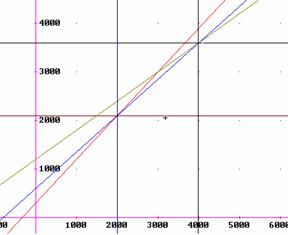
Metto in sistema la prima e la seconda equazione e trovo il primo punto d'intersezione. Successivamente metto la seconda e la terza equazione in sistema e trovo il secondo punto d'incontro.