|
|
| |
Numeri complessi
Un numero complesso Ŕ un numero composto da una parte reale e da una parte immaginaria e si indica con una lettera maiuscola "A".
La parte reale, che si indica con "a", Ŕ costituita da un numero normalissimo.
La parte immaginaria, che
si indica con "jb", Ŕ costituita da un unitÓ
immaginaria "j" che corris 717b19h ponde a![]() , e da un coefficiente della parte immaginaria "b".
, e da un coefficiente della parte immaginaria "b".
J2 = -1 J3 = -J J4 = 1 J5 = J
Con i numeri complessi si possono eseguire delle operazioni:
ADDIZIONE
Questa operazione si esegue sommando le parti reali e poi le parti immaginarie; es:
(a+jb)+(c+jd) = (a+c)+j(b+d)
SOTTRAZIONE
Questa operazione si esegue sottraendo le parti reali e poi le parti immaginarie; es:
(a+jb)-(c+jd) = (a-c)+j(b-d)
MOLTIPLICAZIONE
Questa operazione si esegue come una comunissima moltiplicazione tra binomi; es:
(a+jb)*(c+jd) = ac+jad+jbc+j▓bd = (ac-bd)+j(ad+bc)
DIVISIONE
Questa operazione si esegue moltiplicando numeratore e denominatore per il complesso coniugato del denominatore;
il complesso coniugato di un numero complesso Ŕ un numero che ha la stessa parte reale e parte immaginaria di segno opposto e si indica con una lettera maiuscola con un asterisco "A*"; es:
a+jb c-jd (ac+bd)+J(bc-ad)
![]()
![]()
![]()
c+jd c-jd c2+d2
i numeri complessi si usano per rappresentare dei vettori che si usano nel piano di GAUSS; la parte reale si riporterÓ sulle x e il coefficiente della parte immaginarie sulle y.
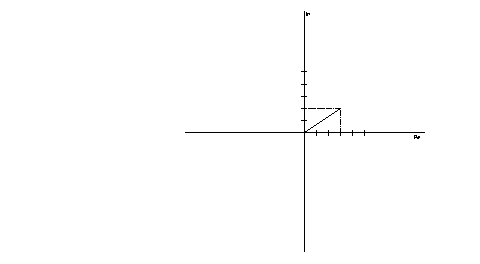
I numeri complessi hanno altre due proprietÓ il modulo e la fase.
Il modulo di un numero complesso Ŕ la lunghezza fisica del vettore che lo rappresenta e si indica con "|A|";
La fase Ŕ l'angolo misurato dall' asse delle x in senso antiorario fino ad incontrare il vettore, esclusivamente in radianti e si indica con A.
A A* = A
A (a2+b2)
A = arctg b/a
e quindi qualsiasi sia l' angolo che risulta dal calcolo dell' arctg il suo valore pu˛ essere sbagliato di p radianti.
Per i numeri complessi esiste un' altra rappresentazione, quella polare o di Eulero che si serve del modulo e della fase; es:
A = A ej A e = numero di Eulero = 2,71
A = a+jb = (a2+b2) eJ arctg b/a
A B = A B ej A+ B)
A/B = A B ej A- B)
FORMULE DI CONVERSIONE
a = A cos A
b = A sin A
A eJ A A cos A + J A sin A
eJx = cosx +sinx
Con i numeri complessi si possono eseguire anche delle espressioni che si risolvono con le operazioni tra numeri complessi giÓ descritte; es:
(3+j2)+(-5+J3) = (-2+J5)
ma si possono anche risolvere in via grafica grazie alla regola del parallelogramma; es:
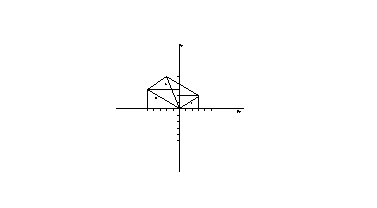
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025