Matematica - L'equazione esponenziale

matematica

Matematica

L'equazione esponenziale

Dati due numeri reali positivi a e N, esiste qualche numero reale x, che, dato per esponente ad a, riproduce il numero N?

a = N

che dicesi equazione esponenziale, poiché l'incognita si trova all'esponente

Questa equazione è risolvibile graficamente, quando sia tracciata la curva esponenziale di equazione y = a . Tracciata la curva esponenziale di equazione y = a e la retta y=N parallela all'asse delle ascisse, il valore richiesto della x è l'ascissa del punto P in cui la retta incontra la curva.

I.   &n 616g69g bsp;   &n 616g69g bsp;   &n 616g69g bsp;   &n 616g69g bsp;  L'equazione esponenziale non ammette soluzioni quando è N<0.

  o x X x o X

Fig 1 Fig2

Dalla fig. 1, per a > 1 si deduce che:

-   &n 616g69g bsp;   &n 616g69g bsp; se 0 < N < 1 è x < 0

-   &n 616g69g bsp;   &n 616g69g bsp; se N =1 è x = 0

-   &n 616g69g bsp;   &n 616g69g bsp; se N > 1 è x > 0

Dalla fig. 2, per 0 < a < 1:

-   &n 616g69g bsp;   &n 616g69g bsp; se 0 < N < 1 è x > 0

-   &n 616g69g bsp;   &n 616g69g bsp; se N = 1 è x = 0

-   &n 616g69g bsp;   &n 616g69g bsp; se N > 1 è x < 0.

Logaritmi

Si è dunque dimostrato che l'equazione a = N ammette sempre una e una sola soluzione, sotto la sola condizione che a e N siano numeri reali positivi ed a diverso dall'unità.

Il numero x che soddisfa l'equazione esponenziale si dice logaritmo del numero N in base a e si denota con

loga N

Il numero N prende il nome di argomento del logaritmo. Le due equazioni: a = N e x = loga N sono equivalenti tra loro.

Il logaritmo di un numero (positivo), in una data base (positiva, diversa da 1), è l'esponente che bisogna dare alla base per ottenere il numero dato.

Così, sfruttando il fatto che:

per a > 0, a 1, b > 0

è x = loga b se e soltanto se è a = b,

si può, per esempio, osservare che l'uguaglianza 2 8 può trasformarsi nell'uguaglianza 3 = log 8, passando così dalla forma esponenziale alla forma logaritmica.

E così, analogamente, sono equivalenti le seguenti forme:

log 1000 = 3 e 10

m = logn p e n = p

1/5 = log e 32 =2

In particolare si noti che dall'uguaglianza a = 1 deriva che 0 è l'esponente da dare alla base a per ottenere 1, cioè:

a loga

Analogamente

a = a loga a = 1.

Si deduce quindi che:

qualunque sia la base, il logaritmo di 1 è uguale a zero e il logaritmo della base è uguale a 1.

Il logaritmo di un numero risulta positivo se la base ed il numero sono entrambi maggiori di 1 o entrambi compresi tra 0 e 1; risulta invece negativo se la base ed il numero sono l'uno maggiore di 1 e l'altro compreso tra 0 e 1 o viceversa.

Ne deriva che:

se la base è maggiore di 1, i numeri maggiori di 1 hanno logaritmi negativi; se la base è minore di 1, i numeri maggiori di 1 hanno logaritmi negativi e quelli minori di 1 logaritmi positivi.

L'insieme di tutti i logaritmi dei numeri positivi in una data base a si chiama sistema di logaritmi a base a.

La curva logaritmica

Si definisce curva logaritmica di base a, il diagramma della funzione

y = loga x,    con a R , a x R

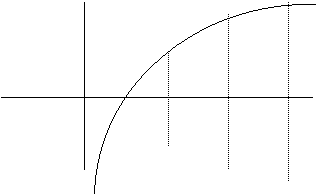
Supponendo che sia a > 1, si ha:

per x = 1, y = loga

per x > 1, y = loga x > 0

per 0 < x < 1, y = loga x < 0

e precisamente quando il numero x > 1 cresce, anche il logaritmo cresce e prendendo x abbastanza grande, il logaritmo diventa frande fin che si vuole. Però attraverso qualche esempio , si vede che il logaritmo cresce più lentamente del numero: per esempio, supposto a = 2, se diamo ad x i valori:

1, 2, 4, 8, 16, .

la y acquista i valori

0, 1, 2, 3, 4, .

Da queste considerazioni ne deriva che la curva logaritmica taglia l'asse delle x nel punto di ascissa 1; alla destra di tale punto è sopra l'asse, dal quale si allontana quando si procede verso destra.

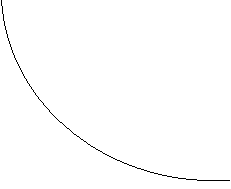
Supponendo invece che 0 <a < 1. in questo caso si ha:

per x = 1, y = loga

per x > 1, y = loga x < 0

per 0 < x < 1, y = loga x > 0

Y a > 1

0 1 X

0 < a < 1

Si può notare che il grafico della funzione con 0 < a <1 oltre a risultare simmetrico rispetto alla bisettrice y = x può considerarsi il simmetrico rispetto all'asse x del grafico della funzione con a >1.

Proprietà dei logaritmi

Qualunque sia la base, i logaritmi godono di importanti proprietà che derivano dalle proprietà delle potenze sfruttando la connessione tra esponenti e logaritmi e sono enunciate nei seguenti teoremi:

1.   &n 616g69g bsp; il logaritmo di un prodotto è uguale alla somma dei logaritmi dei singoli fattori

log ( m · n ) = log m + log n.

2.   &n 616g69g bsp; il logaritmo di un quoziente è uguale alla differenza fra il logaritmo del dividendo e il logaritmo del divisore

log m/n = log m - log n.

3.   &n 616g69g bsp; il logaritmo della potenza di un numero è uguale al prodotto dell'esponente per il logaritmo del numero

log b = m log b.

4.   &n 616g69g bsp; il logaritmo di un radicale è uguale al quoziente del logaritmo del radicando per l'indice della radice.

log = 1/n log b.