SINTESI SULLE SERIE - I limiti notevoli

matematica

I limiti notevoli

Lim

x->0

2) Lim  

x->+

Lim

x->0

Lim 

x->0

Lim  =1

x->+

Lim  = 1

n->+

Lim  =

x->0

Lim   =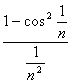

n->0

FORMULE TRIGONOMETRICHE

cos²x + sen²x = 1

sen² x = 1 - cos²x

sen²

LE SERIE NUMERICHE

Una serie numerica è la somma d'infiniti termini.

Rappresentazione:

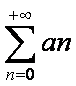a_n = è il termine generale della serie

a₀+a₁+a₂+.......+a_n+......

Lo scopo delle serie numeriche è trovare la somma, più precisamente trovare il carattere della serie. Se la serie da un valore finito è convergente . Se la serie da un valore infinito è divergente. Per sapere se la serie converge o diverge bisogna calcolare il limite del termine generale e in base a cosa tende si saprà come sarà la serie.

CODIZIONE NECCESSARIA PER LA CONVERGENZA

Se il limite del termine generale della serie con n che tende a un numero infinito, è zero,allora la serie numerica può convergere.

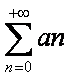
L = 0 converge

Lim a_n=

n L = diverge

SERIE TELESCOPICHE

Le serie telescopiche si riconoscono perché hanno un polinomio scomponibile al denominatore.

Es:

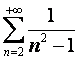
Lim    converge

n

è divergente )

Se q è compreso tra -1 e 1 cioè |q|<1 allora si usa la seguente formula:

S_n =

Invece se la q non è compresa tra -1 e 1 allora si utilizza la seguente formula:

I CRITERI  SUFFICIENTI

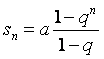
1) CRITERIO DEL RAPPORTO O DI DALAMBER

Il criterio del rapporto viene utilizzato solitamente per le esponenziali e per i fattoriali.

Il criterio del rapporto o di Dalamber dice che data una serie, se il limite per n che tende a + di si hanno tre soluzioni:

l  L < 1 = converge

Lim    L > 1 = diverge

n->+ L = 1 = ? non si sa.

Es:

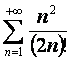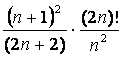    Lim = Lim < 1 la serie è conv.

n->+ n->+

) CRITERIO DEL CONFRONTO

Il criterio del confronto dice che data una serie a_n e b_n e se una delle due è maggiorante dell'altra è convergente si può dimostrare che anche la minorante è convergente.
Se la minorante sarà divergente lo sarà anche l'atra. Vuol dire che si bisogna determinare il carattere della serie.

Es:

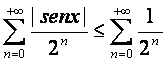è convergente

3) CRITERIO DEL CONFRONTO ASINTOTTICO

Se il limite  delle due sommatori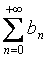e e 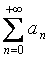è diverso da zero allora hanno

n->+

lo stesso carattere.

Per fare il criterio del confronto asintotico si prende la sommatoria di 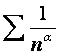dove al variare di a si trovano diverse soluzioni:

a 1 la serie è convergente

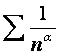a 1 la serie è divergente

Es:

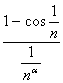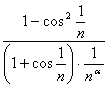  lim = lim =lim 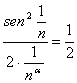per a = 2 conv.

n-> + n-> + n-> +