|
|
| |
LA PROPAGAZIONE DEGLI ERRORI
DIFFERENZA
Date due grandezze, A e B, dimostro che la differenza ha come misura la differenza delle misure e come E (errore) la differenza degli errori.
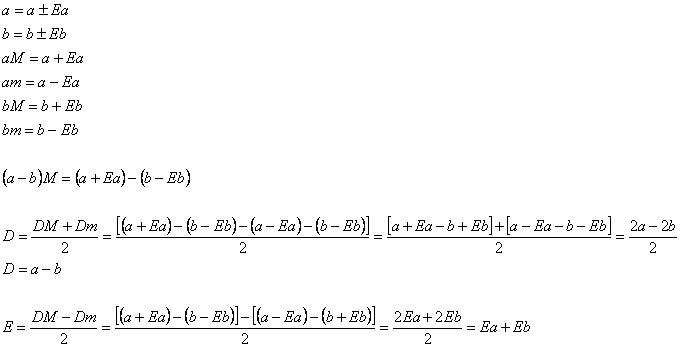

Se moltiplichiamo 757c28h due o più grandezze, l'errore relativo del prodotto è dato dalla somma degli errori relativi dei singoli fattori.
Si può dimostrare che:
la misura del rapporto di due grandezze è uguale al rapporto delle singole misure;
l'errore relativo del rapporto di due grandezze è uguale alla somma degli errori relativi delle singole grandezze.
Ricapitolando:
|
|
|
Nell'addizione e nella sottrazione si sommano direttamente gli errori assoluti. |
|
|
|
|
|
|
|
Nel prodotto di una grandezza per un numero, l'errore assoluto è dato direttamente dal prodotto dell'errore assoluto per il numero stesso. |
|
|
|
Nella moltiplicazione e nella divisione NON si perviene direttamente all'errore assoluto, ma questo deve essere ricavato tenendo presente che all'Er è dato dalla somma degli Er delle singole grandezze. |
|
|
|
|
CONFRONTO DI DUE GRANDEZZE
Se vogliamo dimostrare che le misure di due grandezze sono uguali dobbiamo verificare se l'intersezione dei due intervalli a cui appartengono le due misure non è vuota.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2025