 |  | |
|
| | |
|
| |
MATEMATICA
Illustra il concetto di limite di una funzione reale ad una variabile in tutti i casi possibili, avvalendoti della rappresentazione grafica.
Data una funzione: y = f(x)
con x appartenente
all'insieme dei numeri reali R e
definita in un intervallo (a,b),
riportata la variabile x su una retta
r orientata, ad ogni valore di x
corrisponde un punto P di tale asse e
all'intervallo di definizione della funzione, corrisponde un segmento 
che contiene, nel suo
interno il punto P. Pertanto per
intorno di un punto P di u 757d39h na retta r, si intende l'insieme dei punti, diversi
da P, del segmento contenente P nel suo interno (gli estremi del
segmento possono essere compresi o esclusi). Per intorno destro di P, intendiamo l'insieme dei punti,
diversi da P, di un qualunque
segmento avente P come primo estremo
(il secondo estremo puņ essere compreso o escluso). Per intorno sinistro di P intendiamo l'insieme dei punti,
diversi da P, di un qualunque
segmento avente P come secondo
estremo (il primo estremo puņ essere compreso o escluso).
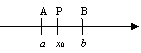
Per intorno di + ∞ si intende l'insieme di tutti i punti della retta r di ascissa maggiore (o maggiore o uguale) di un numero a. Per intorno di - ∞ intendiamo l'insieme di tutti i punti della retta r di ascissa minore (o minore o uguale) di un numero a. Escludendo l'estremo a, si puņ indicare in simboli (a, + ∞), (-∞, a).
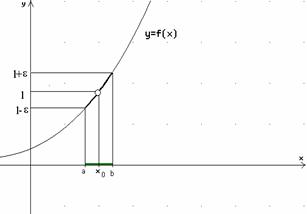
Si dice che la funzione f(x) tende al limite l
(o ha per limite l, o converge ad l) per x tendente ad 
, se posto un numero positivo ε, č possibile determinare
in corrispondenza ad esso un intorno (a,b) di 
, contenuto nell'insieme di definizione della funzione, tale
che per ogni x dell'intorno risulti:
da cui l - ε < f(x) < l+ ε.
In simboli:
Si dice che la funzione f(x) tende a + ∞
(o ha per limite + ∞ o diverge positivamente), per x tendente a , se prefissato liberamente un numero positivo M, abbastanza
grande, si puņ determinare, in corrispondenza ad esso, un intorno (a,b) di , contenuto nell'insieme di definizione della funzione, tale
che per ogni x dell'intorno risulti
f(x)>M.
In simboli:
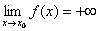
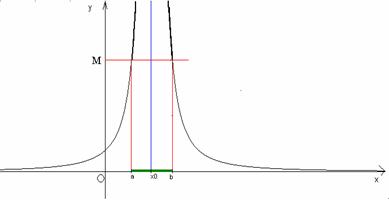
Si dice che la funzione f(x) tende a - ∞ (o ha per limite - ∞o diverge
negativamente), per x tendente a , se prefissato liberamente un numero positivo M, abbastanza
grande, si puņ determinare, in corrispondenza ad esso, un intorno (a,b) di , contenuto nell'insieme di definizione della funzione, tale
che per ogni x dell'intorno risulti
f(x)<-M.
In simboli: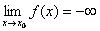 
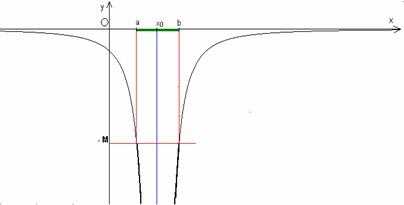
Si dice che la funzione f(x) tende a l (o ha per limite l, o converge ad l) per x tendente a + ∞ [o a - ∞ ], se prefissato ad arbitrio un numero positivo ε, comunque piccolo, č possibile determinare, in corrispondenza ad esso, un intorno (a; + ∞) di + ∞ o [(- ∞;a) di - ∞], contenuto nel dominio della fuzione, tale che per ogni x dell'intorno risulti:
da cui l - ε < f(x) < l+
ε.
In simboli:
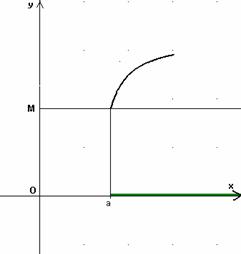
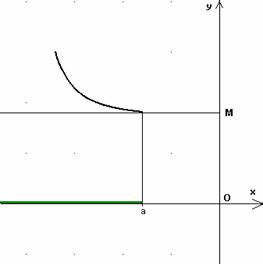
Si dice che la funzione f(x) tende a + ∞, (o che ha per limite + ∞, o che diverge positivamente) per x tendente a + ∞ [o a - ∞], se prefissato ad arbitrio un numero M, abbastanza grande, si puņ determinare in corrispondenza ad esso, un intorno di + ∞ [o di - ∞], contenuto nell'insieme di definizione della funzione, tale cheper ogni x dell'intorno risulti:
f(x)>M
In simboli:
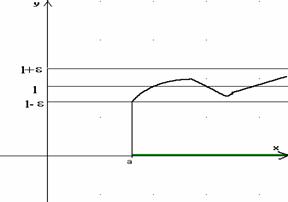
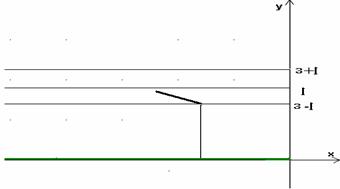
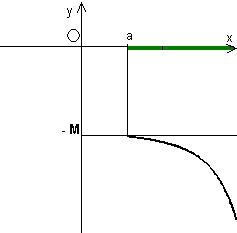
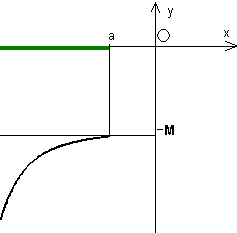
Si dice che la funzione f(x) tende a - ∞, (o che ha per limite - ∞, o che diverge negativamente) per x tendente a + ∞ [o a - ∞], se prefissato ad arbitrio un numero M, abbastanza grande, si puņ determinare in corrispondenza ad esso, un intorno di + ∞ [o di - ∞], contenuto nell'insieme di definizione della funzione, tale che per ogni x dell'intorno risulti:
f(x)<-M
In simboli:
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024
